Математика – это наука, которая изучает числа, формулы, пространство и структуры. Одним из основных инструментов математики являются символы и обозначения, которые помогают нам описывать и анализировать различные математические объекты и операции.
В математике, треугольник перед числом – это математическое обозначение, которое указывает на то, что данное число является функцией или оператором. Треугольник, также известный как "сигма", часто используется в теории чисел и математическом анализе для обозначения суммы ряда или последовательности чисел.
То есть, когда мы видим треугольник перед числом, мы понимаем, что это число должно быть сложено с промежуточными значениями в заданном диапазоне или последовательности чисел. Например, треугольник перед числом может использоваться для обозначения суммы всех натуральных чисел от 1 до этого числа.
Использование треугольника перед числом в математике облегчает запись сложных выражений и помогает нам понять, что данное число связано с операциями суммирования или последовательностями чисел. Важно понимать, как правильно интерпретировать этот символ, чтобы корректно решать математические задачи и проводить исследования в различных областях математики.
Треугольник перед числом в математике

Факториал числа определяется как произведение всех положительных целых чисел от 1 до данного числа. Например, факториал числа 5 равен 5! = 5 × 4 × 3 × 2 × 1 = 120.
Треугольник перед числом имеет значение, что нужно умножить все целые числа, начиная с этого числа и все меньшие числа до 1.
Например:
- 5! = 5 × 4 × 3 × 2 × 1 = 120
- 4! = 4 × 3 × 2 × 1 = 24
- 3! = 3 × 2 × 1 = 6
- 2! = 2 × 1 = 2
- 1! = 1
Треугольник перед числом часто используется в комбинаторике и в задачах с перестановками и сочетаниями. Он также может быть использован в различных математических формулах и выражениях.
Учитывая, что факториал увеличивается очень быстро при увеличении числа, треугольник перед числом обычно используется для облегчения записи больших чисел.
Треугольник перед числом является важным символом в математике и широко используется в различных областях, связанных с комбинаторикой, перестановками, сочетаниями и вероятностями. Знание его значения и правильное понимание его использования поможет в решении сложных математических задач и упростит запись больших чисел.
Значение треугольника в математике

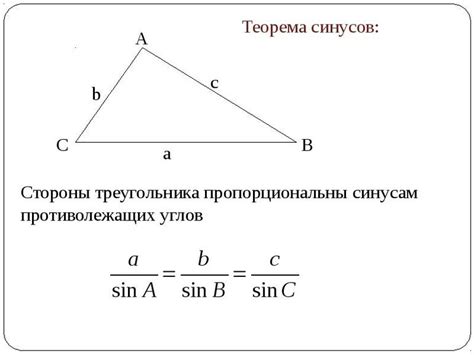
В тригонометрии треугольники используются для изучения соотношений между сторонами и углами. С помощью тригонометрических функций, таких как синус, косинус и тангенс, мы можем вычислять значения углов и сторон треугольника. Также в тригонометрии используется специальный треугольник, известный как "равнобедренный прямоугольный треугольник", который имеет стороны в пропорциях 1:1:√2.
В теории графов треугольник является простым циклом, состоящим из трех вершин и трех ребер. Такие циклы могут играть важную роль при анализе свойств и взаимосвязей между вершинами в графе.
В геометрии треугольник является основной фигурой, от которой можно получить более сложные многоугольники. Одним из важных свойств треугольника является то, что сумма всех его внутренних углов всегда равна 180 градусов. Это свойство может быть использовано для расчета значений углов треугольника, а также для доказательства различных геометрических теорем.
Таким образом, треугольник является важной и многоаспектной фигурой в математике, которая находит применение в различных областях, таких как тригонометрия, теория графов и геометрия.
Применение треугольника в математических уравнениях
Например, уравнение a + b = c означает, что сумма чисел a и b равна числу c. В данном случае треугольник перед знаком равенства указывает на то, что выражения слева и справа от знака равны.
Операция «равно» является основной математической операцией и используется в различных областях математики, начиная с простых арифметических уравнений и заканчивая сложными алгебраическими и тригонометрическими уравнениями.
Важно отметить, что треугольник перед числом может также использоваться для обозначения других операций, например, неравенства (когда два значения не равны друг другу) или принадлежности значений к определенным множествам.
Треугольник перед числом является стандартным математическим обозначением и используется в учебниках, на досках и в математических вычислениях. Он помогает установить связь между различными числами и операциями и сделать математические уравнения более понятными и четкими.
Итак, треугольник перед числом в математике играет важную роль в обозначении операции «равно» и помогает установить связь между выражениями и значениями уравнений.
Использование треугольника в графиках и диаграммах

Треугольники широко используются в графиках и диаграммах для представления различных данных. Этот геометрический символ позволяет наглядно отображать информацию и делает графики более понятными.
Один из наиболее распространенных способов использования треугольника в графиках - это обозначение точек или значений на оси. Часто применяется треугольник, направленный вверх, чтобы показать положительные значения, и треугольник, направленный вниз, для отрицательных значений. Таким образом, треугольники помогают читателю легко интерпретировать данные и сравнить их между собой.
Еще одним способом использования треугольника в графиках и диаграммах является обозначение различных категорий или групп. Каждой категории может быть приписан свой треугольник, что помогает выделить и отличить различные сегменты данных. Это особенно полезно в случаях, когда график представляет собой сложное сравнение или анализ нескольких параметров.
Кроме того, треугольники могут использоваться для обозначения тренда или направления данных. Если треугольник направлен вверх, то это может указывать на положительный тренд или рост. Если треугольник направлен вниз, то это может указывать на отрицательный тренд или снижение. Такая визуализация дает быстрое представление о направлении и динамике данных.
Роль треугольника в геометрии
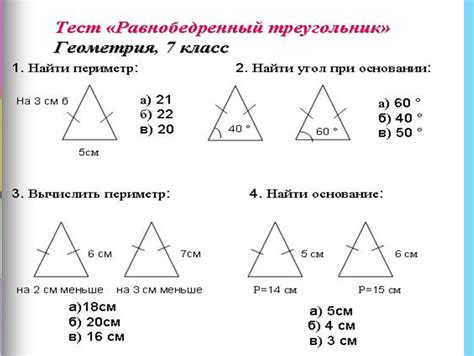
Треугольник определяется как геометрическая фигура, состоящая из трех сторон и трех углов. Он обладает рядом особенностей и свойств, которые позволяют решать различные геометрические задачи.
Одно из простейших свойств треугольника – это сумма внутренних углов треугольника, которая всегда равна 180 градусам. Это свойство называется "сумма углов треугольника".
Также треугольник может быть разными типами в зависимости от свойств его сторон или углов. Например, треугольник может быть равносторонним, если все его стороны равны между собой, или прямоугольным, если один из углов является прямым (90 градусов).
Теоремы и законы, связанные с треугольниками, являются основой для решения самых различных задач, как в геометрии, так и в других областях математики и наук. Некоторые известные теоремы, связанные с треугольниками, включают теоремы Пифагора, синусов и косинусов.
Треугольник является важным элементом в пространственных фигурах и многих разделах геометрии, таких как триангуляция и тригонометрия.
Иными словами, треугольник играет значительную роль в геометрии, обеспечивая основу для изучения различных свойств и теорем, а также предоставляя инструменты для решения различных задач и проблем.
Треугольник как символ в математике и науке

В математике треугольник используется для изучения геометрических свойств и отношений. Он состоит из трех сторон и трех углов, сумма которых всегда равна 180 градусам. Треугольник имеет собственные характеристики, такие как периметр (сумма длин всех сторон) и площадь (измеряемая в квадратных единицах).
В науке треугольник также используется как символ для представления различных концепций. Например, в физике треугольник может означать пропорциональность или зависимость между различными переменными. В химии треугольник может символизировать равновесие между химическими реакциями или состояниями вещества.
Треугольник также является основой для ряда математических теорем, таких как теорема Пифагора, законы синусов и косинусов, а также закон подобия треугольников. Они позволяют решать сложные задачи и находить отношения между сторонами и углами треугольников.



