Угол – это геометрическая фигура, образованная двумя лучами, которые имеют общее начало. Понятие угла является основой в геометрии и широко используется в различных областях науки и техники.
Углы могут быть либо внутренними, либо внешними. Внутренний угол образуется двумя лучами, направленными внутрь фигуры, а внешний угол образуется двумя лучами, один из которых лежит внутри фигуры, а второй – вне ее.
Для определения внутреннего и внешнего угла используется правило правой руки. Если взять правую руку и выставить пальцы вдоль одного из лучей угла, то направление изгиба пальцев покажет, является ли угол внутренним или внешним.
Внутри и вне угла: основные понятия

Внутренний угол – угол, расположенный внутри другого угла и ограниченными им сторонами.
Внешний угол – угол, образованный продолжением одной из сторон угла и другой стороной, лежащей внутри этого угла.
Смежные углы – два угла, имеющие общую сторону и общий внутренний угол.
Вертикальные углы – два угла, имеющие общую вершину и стороны, которые являются продолжениями друг друга.
Сопряженные углы – два угла, сумма которых равна 180 градусам.
Комплементарные углы – два угла сумма которых равна 90 градусам.
Сверхдополнительные углы – два угла, сумма которых равна 360 градусам.
Формула суммы углов треугольника: сумма всех углов треугольника равна 180 градусам.
Угол и его классификация
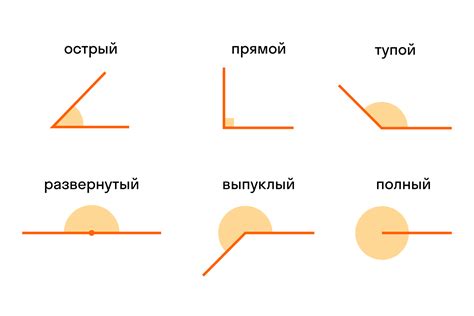
Углы могут быть классифицированы по различным критериям:
По величине: углы могут быть острыми, прямыми, тупыми или полными. Острый угол имеет меньше 90 градусов, прямой - ровно 90 градусов, тупой - больше 90 градусов, а полный угол равен 180 градусам.
По расположению: углы могут быть внутренними или внешними. Внутренний угол находится внутри фигуры, образованной несколькими сторонами, а внешний угол находится снаружи этой фигуры.
По направлению: углы могут быть прямыми, левыми или правыми. Прямой угол имеет горизонтальные лучи, левый угол имеет левый луч, направленный влево, а правый угол имеет правый луч, направленный вправо.
Изучение классификации углов позволяет нам лучше понять их свойства и использовать их в различных математических и геометрических задачах.
Угол в геометрии
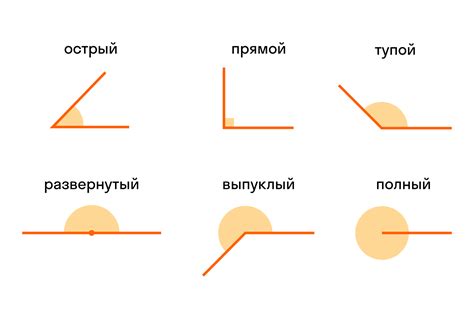
Уголы бывают различных видов и могут иметь разные характеристики. Одной из основных характеристик угла является его величина, которая измеряется в градусах. Величина угла определяется разницей между положением сторон угла относительно друг друга.
Углы бывают прямыми, острыми и тупыми. Прямой угол имеет величину 90 градусов и образуется, когда стороны угла образуют прямую линию. Острый угол имеет величину меньше 90 градусов, а тупой угол - больше 90 градусов.
В геометрии также существуют специальные пары углов. Например, вертикальные углы - это пары углов, которые находятся по разные стороны пересекающихся прямых и имеют равные величины. Смежные углы - это пары углов, которые имеют общую сторону и вершину.
Углы широко используются в разных областях, включая строительство, проектирование, архитектуру и физику. Они позволяют исследовать и описывать формы и пространственные отношения объектов. Понимание углов помогает решать задачи и находить оптимальные решения.
Угол в математическом анализе

В математическом анализе угол это мера поворота прямой на плоскости. Углы могут быть измерены в градусах, радианах или с помощью других единиц измерения. Углы играют важную роль во многих разделах математики и естественных науках.
Угол может быть определен как область между двумя лучами, начинающимися в одной точке. Эта область может быть выражена числовой мерой, которая указывает, насколько далеко прямая повернута. Обычно угол измеряется от 0 до 360 градусов, где 0 и 360 градусов соответствуют параллельным прямым, а 180 градусов - прямому углу.
Углы в математическом анализе используются для определения производной и интеграла функции. Например, производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке. Интеграл функции, с другой стороны, может быть представлен как сумма бесконечно малых углов между касательными, постепенно поворачивающимися от одной точки к другой.
Другие важные понятия, связанные с углами, включают вершины угла (точки начала и конца лучей), стороны (лучи), секундомерные и проходные углы, а также дополнительные углы, сумма которых равна 180 или 90 градусам для прямого угла.
| Градусы | Радианы |
|---|---|
| 0° | 0 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
Исследование углов и их свойств имеет существенное значение для понимания различных математических и физических концепций. Понимание углов позволяет анализировать и предсказывать свойства фигур и движение объектов, а также применять математические методы в различных научных и инженерных областях.
Угол в физике
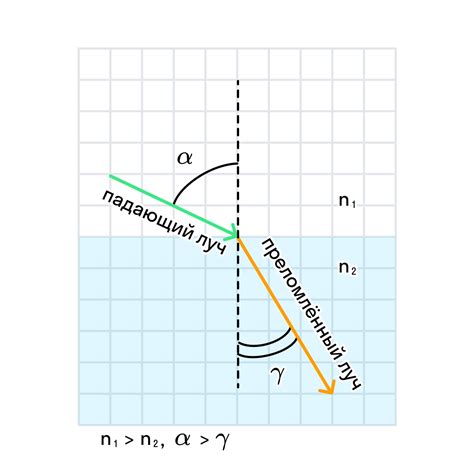
Углы в физике играют важную роль при описании движения, вращения и взаимодействия объектов. Например, при описании векторов сил, угол между векторами определяет направление и эффективность силы, приложенной к объекту.
Кроме того, углы часто используются для измерения различных физических величин, например, скорости вращения, угла отражения света или направления магнитного поля.
Углы в физике также имеют свои основные понятия, такие как острый угол, прямой угол, тупой угол и полный угол. Острый угол имеет значение меньше 90 градусов, прямой угол равен 90 градусам, тупой угол больше 90 градусов, а полный угол равен 360 градусам или 2π радианам.
Понимание углов в физике позволяет ученым и инженерам разрабатывать более эффективные и точные модели и уравнения для описания природных явлений и создания новых технологических решений.
Угол в электронике
В электронике понятие угла используется для описания направления движения электрического тока или расположения электрических компонентов.
Угол в электронике может определяться как фазовый угол, который указывает на разницу во времени или фазе между двумя волнами или сигналами. Фазовый угол часто используется в системах связи, где необходимо синхронизировать передаваемые и принимаемые сигналы.
Кроме того, угол в электронике может указывать на положение электрических компонентов на печатной плате или внутри электронного устройства. Например, при проектировании схемы или макета печатной платы часто важно определить точное местоположение каждого компонента относительно других.
Для измерения и контроля углов в электронике используются специальные инструменты, такие как угломеры и гониометры. Они позволяют определить углы с высокой точностью и использовать их в дальнейших расчетах и проектировании.
Угол в астрономии
Основным единицей измерения углов в астрономии является градус (°). Градус делится на 60 минут (′), а минута - на 60 секунд (″). Такая система измерения углов называется градусно-минутно-секундной (градусная система).
В астрономии углы измеряются по горизонтальной и вертикальной координатам. Горизонтальная система координат используется для указания высоты и азимута объектов на небосводе относительно наблюдателя. Высота измеряется углом от горизонтальной плоскости до объекта (положительные значения - над горизонтом, отрицательные - под горизонтом), а азимут - углом от меридиана до линии, проходящей через наблюдателя и объект (в градусах от 0 до 360).
Вертикальная система координат используется для указания прямого восхождения и склонения объектов на небесной сфере. Прямое восхождение измеряется в часах (от 0 до 24) и указывает положение объекта на небесной сфере в пределах суток. Склонение измеряется в градусах (от -90° до +90°) и указывает положение объекта на небесной сфере относительно экватора.
Углы в астрономии играют важную роль при определении положения небесных тел, навигации в космосе, составлении небесных карт и планировании астрономических наблюдений. Они помогают астрономам лучше понять и изучить Вселенную.
Угол в программировании
В программировании термин "угол" часто используется для описания геометрических фигур и операций с ними. Угол в программировании представляет собой меру поворота вокруг точки или оси и измеряется в градусах или радианах.
В наиболее простом случае угол можно представить с помощью двух векторов, которые образуют его стороны. В программировании эти векторы могут быть представлены в виде координат или угловых значений.
Углы могут использоваться в различных задачах программирования, таких как симуляции движения объектов, отображение элементов интерфейса или расчеты в компьютерной графике. Например, в трехмерной графике углы используются для определения положения и ориентации объектов в пространстве.
В программировании также используются специальные функции и классы для работы с углами, которые позволяют выполнять такие операции как сложение, вычитание, умножение и деление углов.
Понимание понятия угла и умение работать с ними является важным навыком для программистов, особенно для тех, кто занимается разработкой игр, компьютерной графикой или робототехникой.
Угол в программировании представляет собой меру поворота и используется в различных областях программирования. Он позволяет определить положение и ориентацию объектов, выполнять расчеты и симуляции, а также осуществлять сложные операции с углами. Понимание и умение работать с углами является важным навыком для программистов, особенно для тех, кто занимается компьютерной графикой, игровой разработкой или робототехникой.
Угол в психологии

Понятие "угол" в психологии используется в переносном смысле и обозначает определенный аспект внутреннего состояния человека. Угол в психологии может означать внутреннюю напряженность, конфликт или раздражение.
Угол в психологии часто возникает в межличностных отношениях, где человек может сталкиваться с противоречивыми эмоциями и конфликтами. Например, угол может возникнуть в случае несогласия с другим человеком, когда внутреннее состояние человека наполняется раздражением и негативными эмоциями.
Угол в психологии может также возникнуть в результате внутреннего конфликта между разными желаниями, ценностями или представлениями человека. Например, внутренний угол может возникнуть, когда человек сталкивается с выбором между двумя противоположными вариантами действий и испытывает внутреннее напряжение и неопределенность.
Угол в психологии может быть как временным явлением, связанным с определенной ситуацией или эмоциональным состоянием, так и более устойчивым феноменом, связанным с индивидуальными особенностями личности и стилем общения.
Важно отметить, что угол в психологии является естественной реакцией человеческого организма на стрессовые ситуации и конфликты. Однако постоянное нахождение в состоянии угла может привести к негативным последствиям для психического и физического здоровья человека.
Поэтому важно научиться эффективно управлять своими эмоциями и конфликтами, а также развивать навыки психологической гибкости и адаптивности. Это позволит лучше понимать себя и других людей, а также находить более конструктивные способы разрешения конфликтов и достижения гармонии внутри себя и в отношениях с окружающими.



