Геометрия - это раздел математики, который изучает пространственные формы и их свойства. В геометрии есть определенные обозначения, которые позволяют нам удобно работать с фигурами и выполнить точные вычисления. Особенно важно знать значения различных математических знаков, которые используются в геометрии. В этой статье мы рассмотрим основные обозначения и их значения.
В геометрии широко используются знаки для обозначения различных понятий. Знаки могут представляться в виде букв, символов или чисел. Всего таких знаков не так много, но каждый из них имеет свое значение и помогает нам структурировать информацию о фигурах и их свойствах.
Одним из самых важных знаков в геометрии является знак "равно" (=). Этот знак используется для обозначения равенства двух математических выражений или длин отрезков. Например, если у нас есть два отрезка, длины которых равны, мы можем записать это как AB = CD, где AB и CD - это имена отрезков, а равно (=) означает, что их длины совпадают.
Знак "плюс" (+) используется в геометрии для обозначения сложения длин отрезков или углов. Например, если мы хотим вычислить сумму двух углов, мы можем записать это как ∠ ABC + ∠ CDE = ∠ ADE, где ∠ ABC, ∠ CDE и ∠ ADE - это имена углов, а плюс (+) означает, что мы складываем их величины.
Линия: виды и значения
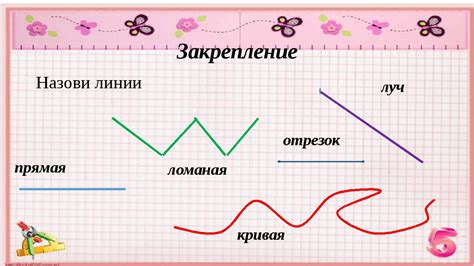
В таблице ниже представлены основные виды линий, их обозначения и значения:
| Вид линии | Обозначение | Значение |
|---|---|---|
| Прямая линия | AB или m | Непрерывная линия, которая не имеет конца и направлена в обе стороны |
| Отрезок | AB | Часть прямой линии, ограниченная двумя точками A и B |
| Луч | →AB или √ | Часть прямой линии, которая имеет начало в точке A и простирается в бесконечность в одном направлении |
| Кривая | C | Линия, которая не является прямой и имеет изогнутую форму |
Знание основных обозначений и значений линий позволяет легче ориентироваться в геометрических задачах и решать их более эффективно.
Отрезок: определение и свойства

Отрезок обозначается двумя его концами. Например, отрезок с концами А и В можно обозначить как АВ или ВА.
Отрезок имеет определенную длину, которая измеряется в единицах длины, например, в сантиметрах или метрах. Длина отрезка может быть вычислена с помощью формулы расстояния между двумя точками.
Отрезок имеет несколько свойств:
- Отрезок всегда прямой и неизогнутый.
- Длина отрезка всегда положительна.
- Всякая точка на отрезке находится между его концами.
- Отрезки могут быть равными или неравными.
- Отрезки могут иметь пересечения между собой.
- Если два отрезка имеют одну общую точку, то они называются соседними отрезками.
Отрезки широко используются в геометрии для измерения и описания различных объектов, таких как фигуры, прямые, углы и т.д.
Полупрямая: геометрическое представление и особенности
Особенность полупрямой заключается в том, что у нее есть начальная точка, но она не имеет конечной точки. Полупрямая обозначается одной буквой, обычно прописной, и над ней ставится стрелка, указывающая направление продолжения линии.
Полупрямая может быть направлена влево или вправо. Если стрелка направлена влево, то полупрямая называется левосторонней, а если стрелка направлена вправо, то - правосторонней.
Полупрямая может быть представлена числами. Начальная точка полупрямой обозначается буквой, а расположение других точек на полупрямой задается числом, которое показывает, насколько эти точки удалены от начальной точки в положительном направлении.
Прямая: основные характеристики и примеры

Направление прямой – горизонтальное, вертикальное или наклонное. Горизонтальная прямая ориентирована в горизонтальном направлении и не имеет наклона. Вертикальная прямая перпендикулярна горизонтальному направлению и не имеет наклона в горизонтальной плоскости. Наклонная прямая имеет угол наклона относительно горизонтального или вертикального направления.
Длина прямой измеряется в единицах длины, таких как сантиметры или метры. Положение прямой может быть задано относительно других фигур, например, параллельно другой прямой или пересекающей ее.
Примеры прямых в повседневной жизни включают прямые линии на страницах книги, ребра прямоугольника или квадрата, стоечки в заборе или прямые полосы на дороге.
Угол: классификация и значимость
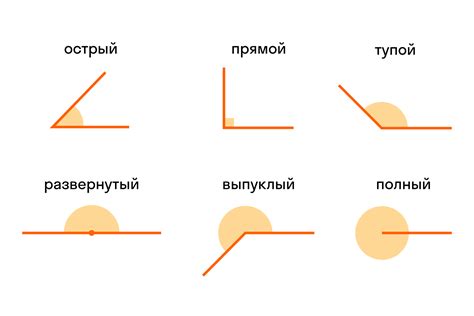
Углы классифицируются по нескольким признакам:
| Классификация | Описание |
|---|---|
| Острый угол | Угол, меньший прямого угла (меньше 90 градусов) |
| Прямой угол | Угол, равный 90 градусам |
| Тупой угол | Угол, больший прямого угла (больше 90 градусов и меньше 180 градусов) |
| Разносторонний угол | Угол, у которого все стороны разные |
| Равнобедренный угол | Угол, у которого две стороны равны |
| Противолежащие углы | Углы, стороны которых являются продолжениями друг друга иобразуют боковую ветвь пересекающейся прямой |
Значимость углов в геометрии заключается в их роли в решении геометрических задач и построений. Углы используются для измерения поворотов, определения соотношений между линиями и плоскостями, а также для расчета площадей и объемов фигур. Они служат основой для доказательства геометрических теорем и применяются при исследовании различных геометрических фигур и фигур в пространстве.
Помимо геометрии, углы находят применение в различных областях знания, таких как архитектура, физика, компьютерная графика, навигация и многие другие. Они используются для измерения, описания и представления поворотов объектов и процессов, позволяют определить области видимости, направление движения и множество других важных характеристик.
Параллельные прямые: определение и свойства

Основные свойства параллельных прямых:
1. Углы между параллельными прямыми
Углы, образованные параллельными прямыми, равны между собой. Если точки A, B и C лежат на одной прямой, а прямые AB и BC параллельны, то угол ABC равен углу BAC.
2. Углы с прямыми
Пересекая параллельные прямые, мы получаем специальные пары углов. Углы, лежащие на одной стороне от пересекающей их прямой и между параллельными прямыми, называются сопряженными внутренними. Они равны.
Углы, лежащие на разных сторонах от пересекающей прямой и между параллельными прямыми, называются сопряженными внешними. Они также равны.
3. Конструкции с параллельными прямыми
Параллельные прямые имеют важное значение в геометрических конструкциях. Используя параллельные прямые, мы можем построить равные углы, равные отрезки и другие фигуры.
Параллельные прямые играют важную роль в геометрии и математике в целом. Они помогают в решении различных задач и представляют основу для изучения геометрических форм и пространства.
Перпендикулярные прямые: основные характеристики
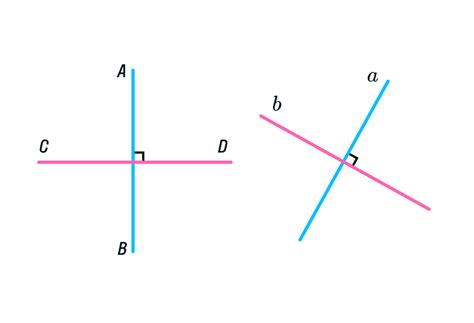
1. Угол между перпендикулярными прямыми всегда равен 90 градусам. Это значит, что в точке пересечения прямых образуется прямой угол.
2. На одной из перпендикулярных прямых можно построить высоту треугольника. Высота является отрезком, проведенным из вершины треугольника до прямой, содержащей противоположную сторону и перпендикулярной к ней.
3. Перпендикулярные прямые делят плоскость на четверти. В каждой четверти находится определенный набор точек, которые находятся по одну сторону от обеих перпендикулярных прямых.
4. Отрезки, соединяющие точки пересечения перпендикулярных прямых с прямыми, параллельными одной из них, равны между собой. Это значит, что расстояние от точки пересечения до параллельной прямой на каждой стороне равно.
5. Перпендикулярные прямые имеют одинаковый наклонный коэффициент, обратно пропорциональный. Наклонный коэффициент - это отношение изменения y-координаты к изменению x-координаты на прямой.
В общем, перпендикулярные прямые являются важным элементом в геометрии и используются для решения различных задач, например, для построения высоты треугольника или определения расстояния между точками в плоскости.
Площадь: расчет и практическое применение

Для различных фигур существуют конкретные формулы для расчета площади. Например, для прямоугольника площадь равна произведению длины одной стороны на длину другой. Для треугольника площадь можно вычислить, используя формулу полупериметра и радиуса вписанной окружности. Для круга площадь равна квадрату радиуса, умноженного на число Пи.
Расчет площади не только позволяет определить размер фигуры, но и находит практическое применение в различных областях. Например, зная площадь прямоугольного поля, можно рассчитать количество семян или растений, необходимых для его посева. Площадь квартиры или комнаты поможет нам определить объем необходимой мебели или степень освещенности помещения. В архитектуре и строительстве расчет площади является необходимым элементом при проектировании и определении стоимости строительных материалов.
Помимо простых формул, существуют и сложные методы для расчета площади фигур с нестандартной формой или с выступающими элементами. В таких случаях можно разбить фигуру на несколько простых фигур, вычислить площадь каждой из них и сложить их значения вместе.
Использование понятия площади и умение правильно расчитывать ее значение являются важными навыками как в геометрии, так и в повседневной жизни. Расчет площади позволяет нам лучше понять и оценить размеры и форму фигур, а также применять полученные значения в различных практических ситуациях.
Объем: определение и способы вычисления
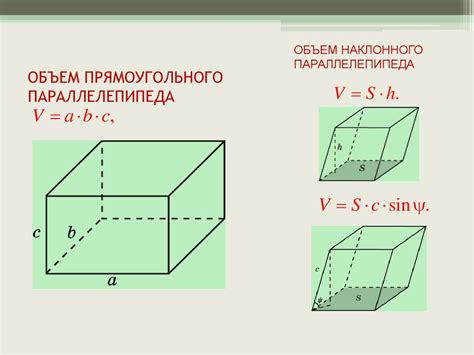
Объем позволяет определить, сколько места занимает объект.
Объем можно вычислить для различных трехмерных фигур, таких как параллелепипеды, призмы, цилиндры и шары.
Каждая фигура имеет свою формулу для расчета объема, которая основывается на ее геометрических характеристиках.
Один из способов вычисления объема – использование основных формул для различных фигур.
Например, для параллелепипеда формула для расчета объема будет следующей: объем = длина × ширина × высота.
Еще один способ определения объема – разбиение фигуры на более простые формы,
для которых уже известны формулы объема. Затем полученные значения объема складываются или вычитаются,
чтобы получить общий объем исходной фигуры.
Независимо от способа вычисления, объем измеряется в кубических единицах, таких как кубический метр (м³), кубический сантиметр (см³), кубический дециметр (дм³) и т. д.
Формулы в геометрии: основные уравнения и их решения

Одним из ключевых понятий в геометрии является понятие уравнения. Уравнение в геометрии – это математическое выражение, связывающее различные параметры и свойства фигуры. Решение уравнения позволяет найти конкретные значения параметров или определить свойства фигуры.
В геометрии существует множество различных уравнений, которые применяются для решения разных задач. Некоторые из основных уравнений в геометрии включают:
1. Уравнение прямой: y = mx + b, где m – коэффициент наклона прямой, b – свободный член.
2. Уравнение окружности: (x - a)^2 + (y - b)^2 = r^2, где (a, b) – координаты центра окружности, r – радиус окружности.
3. Уравнение параболы: y = ax^2 + bx + c, где a, b и c – коэффициенты параболы.
Решение уравнений в геометрии может иметь различные формы в зависимости от поставленной задачи. Например, решая уравнение прямой, мы можем найти ее угловой коэффициент и свободный член, а также найти точки пересечения с другими прямыми или фигурами. Решая уравнение окружности, мы можем определить ее радиус и координаты центра, а также найти точки пересечения с другими окружностями или прямыми. Решая уравнение параболы, мы можем найти ее вершину, фокус, а также найти точки пересечения с другими параболами или прямыми.
Использование уравнений в геометрии позволяет анализировать и решать разнообразные задачи, связанные с геометрическими фигурами. Понимание основных уравнений и их решений является важным навыком при изучении геометрии и применении ее в практических задачах.



