В математике одним из основных понятий, изучаемых в начальной школе, является понятие стороны. Сторона – это одна из линий, образующих геометрическую фигуру. В пятом классе знание о сторонах важно для понимания различных геометрических фигур и их свойств.
Основная особенность понятия сторона заключается в том, что оно применимо к самым разным объектам. Стороны можно найти у треугольников, прямоугольников, квадратов, параллелограммов, букв "Л" и "П", ромбов и многих других фигур. Более того, понятие стороны применимо и вне геометрии – например, в физике при изучении сторон угла или грани тела.
Для каждой геометрической фигуры стороны имеют свои характеристики и особенности. Например, у квадрата все стороны равны между собой, а у прямоугольника две противоположные стороны равны. Понимание этих особенностей позволяет легче разбираться в задачах и находить решения.
Структура и определение стороны
Структура стороны включает в себя:
| Точки | Сторона определяется двумя точками, которые являются конечными точками данной стороны. Эти точки могут быть обозначены буквами, например, точка А и точка В. |
| Отрезок | Сторона также может быть представлена отрезком, который является прямой линией, соединяющей две точки. Длина этого отрезка является мерой данной стороны. |
| Направление | Сторона имеет направление от первой точки ко второй точке. Это направление может быть указано стрелками или символами, указывающими на порядок движения. |
Сторона в геометрии может быть прямой или кривой. При работе со сторонами, важно помнить, что они могут быть частью фигуры, такой как треугольник или квадрат, и могут быть связаны друг с другом с помощью углов.
Определение стороны в математике помогает нам разбираться в формах, измерять расстояния и строить различные геометрические фигуры.
Свойства сторон

Она имеет следующие свойства:
| Вершины | Страница обладает двумя вершинами. Каждая вершина является началом и концом стороны. |
| Длина | Длина стороны равна расстоянию между ее вершинами. |
| Продолжение | Страница можно продлить в обе стороны до бесконечности. |
Запомни эти свойства, они помогут тебе лучше понять и использовать понятие стороны в математике.
Различные виды сторон
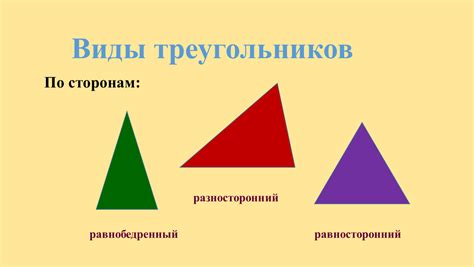
В зависимости от типа фигуры, сторона может иметь свои характеристики и особенности. Рассмотрим некоторые из них:
| Фигура | Характеристики сторон |
|---|---|
| Квадрат | Все стороны равны друг другу по длине. Углы между сторонами равны 90 градусов. |
| Прямоугольник | Две пары сторон равны друг другу по длине. Углы между сторонами равны 90 градусов. |
| Ромб | Все стороны равны друг другу по длине. Углы между сторонами не обязательно равны 90 градусов. |
| Треугольник | Три стороны могут быть разной длины. Углы между сторонами в сумме равны 180 градусов. |
| Окружность | Окружность не имеет сторон в привычном понимании. Однако, можно считать, что окружность состоит из бесконечного числа очень коротких сторон (касательных), которые образуют ее окружность. |
Это лишь некоторые из примеров различных видов сторон в геометрии. Изучение свойств сторон помогает понять особенности различных фигур и решать задачи на их основе.
Зависимость между сторонами
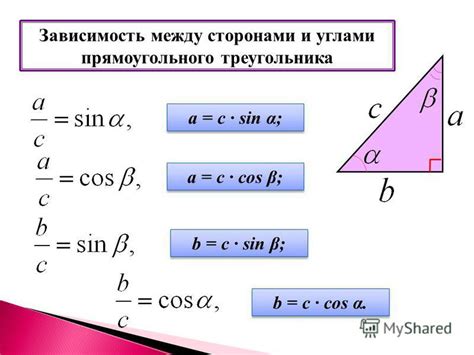
В математике, стороны многоугольника представляют собой его отрезки, которые соединяют вершины и образуют его грани. Стороны многоугольника могут иметь различные длины, и в зависимости от этих длин может меняться его внешний вид и свойства.
Зависимость между сторонами многоугольника основана на их длинах и углах, которые образуют эти стороны. Например, в прямоугольнике две стороны называются его основаниями, а две другие стороны - его боковыми сторонами. Основания прямоугольника имеют равные длины, а боковые стороны также равны между собой. Это делает прямоугольник четырехугольником с определенными свойствами и отличает его от других многоугольников.
Однако стороны многоугольника могут быть разными, и при этом сохранять определенную зависимость между собой. Например, в треугольнике сторона, противолежащая наименьшему углу, всегда будет иметь наименьшую длину, а сторона, противолежащая наибольшему углу, всегда будет иметь наибольшую длину.
Знание зависимости между сторонами многоугольника позволяет анализировать и решать различные математические задачи, связанные с геометрией и конструированием. Понимание этой зависимости помогает лучше понять и использовать принципы математики в решении практических задач.
Примеры задач на стороны

Задача 1: В треугольнике ABC стороны имеют длины 5, 6 и 7. Найдите периметр треугольника.
Решение: Периметр треугольника вычисляется как сумма длин его сторон. В данном случае, периметр треугольника ABC равен 5 + 6 + 7 = 18.
Задача 2: В треугольнике XYZ сторона XY имеет длину 9, а стороны XZ и YZ равны по 5. Найдите периметр треугольника.
Решение: Периметр треугольника XYZ равен сумме длин всех его сторон. В данном случае, периметр треугольника XYZ равен 9 + 5 + 5 = 19.
Задача 3: В прямоугольнике ABCD сторона AB равна 8, а сторона BC равна 5. Найдите периметр прямоугольника.
Решение: Периметр прямоугольника вычисляется как удвоенная сумма его сторон. В данном случае, периметр прямоугольника ABCD равен 2 * (8 + 5) = 2 * 13 = 26.
Задача 4: В параллелограмме PQRS стороны PQ и RS равны по 7, а сторона PS равна 9. Найдите периметр параллелограмма.
Решение: Периметр параллелограмма вычисляется как удвоенная сумма его сторон. В данном случае, периметр параллелограмма PQRS равен 2 * (7 + 7 + 9) = 2 * 23 = 46.
Задача 5: В трапеции ABCD боковые стороны AB и CD равны по 4, а основания AD и BC равны по 6. Найдите периметр трапеции.
Решение: Периметр трапеции вычисляется как сумма длин всех её сторон. В данном случае, периметр трапеции ABCD равен 4 + 6 + 4 + 6 = 20.



