При изучении числовых промежутков в математике можно столкнуться с таким понятием, как "закрашенная точка". Этот символ широко используется для обозначения включительности или исключительности границ промежутка.
Закрашенная точка обычно используется вместе с другими математическими символами, такими как неравенства или равенства. Если закрашенная точка находится на границе промежутка, то это означает, что данная граница включена в промежуток. В других случаях, когда точка не закрашена, она означает, что граница промежутка не включается.
Использование закрашенной точки позволяет точно определить, включена ли граница промежутка в рассматриваемое множество значений. Такая ясность является важным элементом в математике, где точное определение промежутков и множеств является основой для дальнейших рассуждений и вычислений.
Значение закрашенной точки в числовом промежутке

В математике и анализе числовых промежутков, закрашенная точка обозначает принадлежность значения точке на числовой оси.
Одномерная числовая ось может быть представлена в виде промежутка с началом и концом, а также возможными значениями между ними. Закрашенная точка указывает на то, что значение, соответствующее указанной точке, входит в данный числовой промежуток.
Для визуального обозначения закрашенной точки в числовом промежутке обычно используется отрезок с закрашенным кружком или точкой на конце. Это помогает понять, что указанное значение включается в промежуток и является его частью.
Например, если имеется числовой промежуток от 1 до 5 и точка 3 закрашена, это означает, что значение 3 входит в данный промежуток. То есть, числа от 1 до 5 включительно.
| Промежуток | Значение | Точка |
|---|---|---|
| [1, 5] | 3 | ● |
Если точка не закрашена, то значение не включается в промежуток. Например, в промежутке [1, 5) значение 5 не включается, так как круглая скобка указывает на то, что конечное значение не входит в промежуток.
| Промежуток | Значение | Точка |
|---|---|---|
| [1, 5) | 5 | ○ |
Закрашенная точка в числовом промежутке позволяет более точно определить включение или исключение соответствующего значения в промежуток, улучшая понимание и работу с числовыми интервалами.
Понятие закрашенной точки
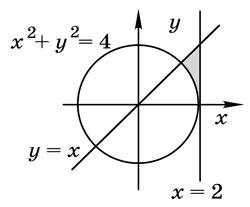
В математике промежутки представляются в виде отрезков или интервалов. Отрезок - это промежуток, который включает все числа между двумя конечными точками, включая сами эти точки. В отличие от отрезка, интервал - это промежуток, который включает все числа между двумя конечными точками, но не включает сами эти точки.
Закрашенная точка указывает, что данное число принадлежит промежутку. Например, если имеется промежуток [2, 5], то закрашенная точка на числовой оси между числами 2 и 5 указывает, что все значения между этими числами, а также сами эти числа, включены в промежуток.
Закрашенные точки используются для обозначения интервалов и отрезков на числовой оси, что позволяет более наглядно представить математические промежутки и их взаимоотношения.
Важно отметить, что закрашенные точки могут использоваться не только на числовой оси, но и в других контекстах, где требуется указать принадлежность значения к определенному промежутку или интервалу.
Использование закрашенной точки в математике

Для того чтобы понять, как использовать закрашенную точку, необходимо знать, что в математике промежутки могут быть открытыми и закрытыми. Открытый промежуток не включает границы, а закрытый промежуток включает их.
В случае открытого промежутка, границы обозначаются незакрашенными точками или круглыми скобками. Например, (а, б) означает открытый промежуток между значениями а и б, не включая самых границ.
В случае закрытого промежутка, границы обозначаются закрашенными точками или квадратными скобками. Например, [а, б] означает закрытый промежуток между значениями а и б, включая самые границы.
Использование закрашенной точки позволяет явно указать, что границы промежутка включены в рассматриваемый интервал. Например, если имеется промежуток [3, 7], то это означает, что все числа, начиная с 3 и заканчивая 7, включительно, принадлежат данному промежутку.
Таким образом, закрашенная точка в числовом промежутке является важным элементом математической нотации, позволяющим четко указать, включены ли границы промежутка или нет. Она означает, что граница промежутка включена в рассматриваемый интервал и имеет значение на данном промежутке.
Практические примеры применения закрашенной точки
Закрашенная точка в числовом промежутке обычно используется для обозначения, что данная точка включена в указанный промежуток. Рассмотрим несколько практических примеров его применения:
- В линейной алгебре закрашенная точка может указывать на то, что конкретное значение входит в определенный промежуток чисел или множество.
- На числовой оси, если точка закрашена, она включается в интервал. Например, если у нас есть интервал от 0 до 5, и точка 3 закрашена, это означает, что значение 3 также включено в данный интервал.
- В математических уравнениях, закрашенная точка может использоваться для обозначения корней или решений уравнений.
- Использование закрашенной точки может быть полезно при представлении графиков на числовой оси, чтобы показать, где находятся включенные значения.
- В неравенствах, закрашенная точка может указывать на то, что данное значение входит в диапазон, заданный неравенством.
Все эти примеры демонстрируют, как закрашенная точка может помочь визуально обозначить, какие значения включены в определенный числовой промежуток или множество, что является важным элементом при работе с числами и математическими концепциями.
Закрашенная точка и интервалы
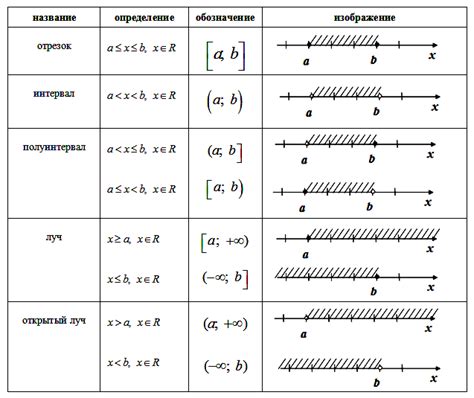
В математике закрашенная точка на числовой оси обозначает, что данная точка включена в числовой промежуток.
Числовые промежутки представляют собой отрезки на числовой оси и используются для обозначения интервалов значений переменных. Квадратная скобка, которая обозначает закрашенную точку, указывает на то, что граница промежутка включена в интервал.
Например, если имеется числовой промежуток [2, 5], это означает, что в интервал включены все числа от 2 до 5, включительно. Закрашенная точка на каждой границе показывает, что границы промежутка включены в интервал.
Если требуется указать интервал, включающий все числа между двумя значениями, квадратные скобки можно заменить на круглые скобки. Например, (0, 1) обозначает интервал всех чисел, кроме 0 и 1.
Закрашенная точка на числовой оси позволяет наглядно представить, включены ли конкретные значения в числовой промежуток. Использование закрашенных точек и скобок является важным инструментом для понимания и работы с интервалами на числовой оси.
Закрашенная точка в графиках и диаграммах
Закрашенная точка в числовом промежутке представляет собой графическое обозначение определенного значения на оси координат. Она часто используется в графиках и диаграммах для визуализации данных и их анализа.
Закрашенная точка может иметь различные цвета и размеры, которые зависят от стиля и дизайна графика или диаграммы. Обычно она обозначает определенное значение или категорию данных.
Например, в столбчатой диаграмме закрашенные точки могут представлять собой высоту столбца, что помогает сравнивать и анализировать различные значения на оси координат. В линейной диаграмме закрашенная точка может означать конкретные значения, показывая тренд или изменение данных во времени.
В целом, закрашенная точка в графиках и диаграммах является эффективным средством для визуализации данных и представления информации. Она позволяет улучшить понимание данных, выделять важную информацию и сравнивать различные значения.
Закрашенная точка в программировании
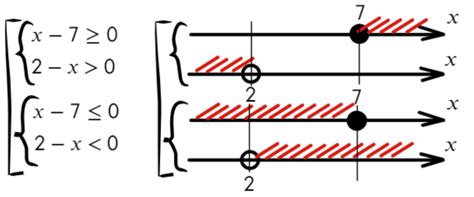
(a, b) ⇒ промежуток не включает a и b
[a, b] ⇒ промежуток включает a и b
(a, b] ⇒ промежуток включает b, но не включает a
[a, b) ⇒ промежуток включает a, но не включает b
Такое обозначение используется в различных контекстах программирования, например, при работе с условными операторами или функциями, которым необходимо указывать промежутки значений.
Это важно учитывать при анализе и написании кода, чтобы избежать возможных ошибок и недоразумений в работе программы.
Другие области применения закрашенной точки
Закрашенная точка в числовом промежутке используется не только в математике, но и в других областях:
1. Графика и дизайн: Закрашенная точка может быть использована в графическом дизайне для обозначения конкретной точки на экране или на плоскости. Она может использоваться для создания эффекта визуальной акцентуации в дизайне интерфейсов, визуализации данных и в других графических проектах.
2. Картография: В картографии закрашенная точка может быть использована для обозначения конкретного места, объекта или точки интереса на карте. Она может служить для указания местоположения города, ориентира, достопримечательности или других важных точек.
3. Научные исследования: Закрашенная точка в числовом промежутке может быть использована для обозначения значимых моментов или событий в хронологическом порядке. Она может служить для обозначения начала или конца периода, точки изменения тренда, критических событий и других важных событий или феноменов в научных исследованиях.
4. Игровая индустрия: В видеоиграх закрашенная точка может использоваться для обозначения пути игрока, места назначения, объектов или препятствий на игровом поле. Она может служить визуальным маркером для игрока, указывая на следующую цель или задание.
5. Информационные технологии: В информационных системах и программных приложениях закрашенная точка может быть использована для обозначения выполненных или активных элементов интерфейса, шагов в процессе, выбранных параметров или действий пользователя. Она может помочь визуально ориентироваться пользователю и обозначать текущее состояние или выбранное значение.
Все эти области применения показывают гибкость и универсальность закрашенной точки в числовом промежутке, которая позволяет использовать ее для различных целей в разных контекстах.



