Закон сохранения энергии – один из фундаментальных законов физики, играющий важную роль в механике. Этот закон утверждает, что энергия не может быть создана или уничтожена, а может только превращаться из одной формы в другую. Таким образом, сколько бы энергии ни было в системе, ее общая сумма остается постоянной.
Основное положение закона сохранения энергии стало известно благодаря исследованиям немецкого физика Германа Гельмгольца в середине XIX века. Он ввел понятие полной механической энергии, которая представляет собой сумму кинетической и потенциальной энергий системы. Кинетическая энергия связана с движением тела, а потенциальная – с его положением в поле сил. Гельмгольц показал, что полная энергия в замкнутой системе остается постоянной во время всех процессов.
Принцип сохранения энергии является одним из базовых принципов механики, наравне с принципами наилучшего времени и наименьшего действия. Он находит широкое применение в различных областях физики, включая механику твёрдого тела, гидродинамику, электродинамику и квантовую механику. Благодаря закону сохранения энергии можно решать сложные задачи, связанные с движением тел и взаимодействием между ними, внося некоторые упрощения и находя общие закономерности.
Кинетическая энергия и потенциальная энергия: основные понятия и различия

Кинетическая энергия связана с движением тела и определяется его скоростью. Она выражает способность тела совершать работу за счет своего движения. Кинетическая энергия зависит от массы тела и его скорости. Математически она выражается формулой:
К = (1/2)mv^2
где K – кинетическая энергия, m – масса тела, v – скорость тела.
Пример: Если мяч массой 0,5 кг движется со скоростью 10 м/с, то его кинетическая энергия равна 25 Дж.
Потенциальная энергия связана с положением тела относительно других тел или положением внутри гравитационного поля. Она выражает способность тела совершать работу за счет своего положения. Потенциальная энергия зависит от массы тела, силы тяжести и высоты положения. Математически она выражается формулой:
П = mgh
где П – потенциальная энергия, m – масса тела, g – ускорение свободного падения (около 9,8 м/с^2), h – высота положения.
Пример: Если предмет массой 1 кг находится на высоте 5 метров, то его потенциальная энергия равна 49 Дж.
Разница между кинетической и потенциальной энергией заключается в их смысле и проявлении. Кинетическая энергия связана исключительно с движением тела, тогда как потенциальная энергия связана с его положением в пространстве и его взаимодействием с гравитацией или другими телами. Кинетическая энергия всегда положительна и может быть полностью преобразована в другие виды энергии, например, в потенциальную или тепловую. Потенциальная энергия может быть положительной или отрицательной, в зависимости от выбора нулевого уровня. Они взаимосвязаны и могут превращаться друг в друга, согласно закону сохранения энергии.
Механическая энергия и ее виды

Механическая энергия представляет собой сумму кинетической и потенциальной энергии системы.
Кинетическая энергия - это энергия движения тела. Она определяется массой тела и его скоростью. Формула для расчета кинетической энергии выглядит следующим образом:
КЭ = (mv2)/2
где КЭ - кинетическая энергия, m - масса тела, v - скорость тела.
Потенциальная энергия - это энергия, связанная с положением тела относительно других тел или положением внутри поля. Существует несколько видов потенциальной энергии:
| Вид потенциальной энергии | Формула |
|---|---|
| Потенциальная энергия упругой деформации | ПЭупр = (kx2)/2 |
| Потенциальная энергия гравитационного поля | ПЭгр = mgh |
| Потенциальная энергия электрического поля | ПЭэл = kq1q2/r |
где ПЭ - потенциальная энергия, k - коэффициент, х - максимальное отклонение (для упругой деформации), m - масса, g - ускорение свободного падения, h - высота (для гравитационного поля), q1 и q2 - заряды, r - расстояние (для электрического поля).
При законе сохранения энергии в механике, механическая энергия является константой. Система может переходить из одного вида энергии в другой, но общая сумма энергии остается неизменной.
Закон сохранения энергии: формулировка и принцип действия
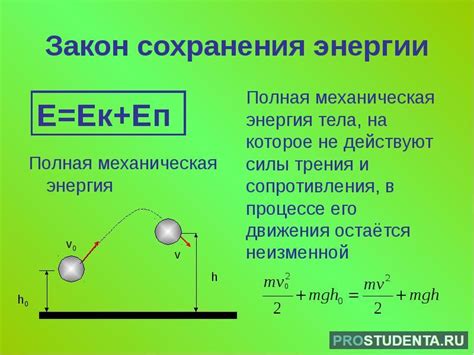
Закон сохранения энергии в механике формулируется следующим образом: сумма кинетической и потенциальной энергии замкнутой системы остается постоянной во времени, если на нее не действуют внешние силы.
Принцип действия закона сохранения энергии основывается на принципе работы исключительно консервативных сил. Консервативные силы таковы, что работа, совершенная ими, не зависит от пути, по которому происходит перемещение тела в поле силы, а зависит только от начального и конечного положений тела. Это означает, что у консервативных сил существует потенциальная энергия, которая может быть преобразована в кинетическую энергию и наоборот. При этом, сумма кинетической и потенциальной энергии остается постоянной.
Закон сохранения энергии широко используется в механике для решения задач, связанных с движением тел и их взаимодействием. С его помощью можно определить скорость и положение тела в любой момент времени, а также оценить энергетические характеристики системы.
Таким образом, закон сохранения энергии является фундаментальным принципом, согласно которому энергия в системе является постоянной и может только изменять свою форму. Этот закон позволяет понять различные аспекты динамики и взаимодействия механических систем и является неотъемлемой частью физической науки.
Консервативные и неконсервативные силы: разница и их влияние на сохранение энергии

Одним из примеров консервативных сил является сила тяжести. При движении объекта в поле тяжести, потенциальная энергия системы изменяется, но ее сумма остается постоянной. Это связано с тем, что сила тяжести зависит только от расположения объекта в поле и не зависит от его скорости.
Неконсервативные силы - это силы, приложенные к объекту, которые зависят от его скорости или ускорения. Такие силы могут приводить к потере или преобразованию механической энергии системы.
Примеры неконсервативных сил включают силу трения, силу сопротивления воздуха и силу тяги двигателя. В отличие от консервативных сил, неконсервативные силы могут приводить к потере механической энергии системы в виде тепловой энергии или других форм энергии.
Влияние консервативных и неконсервативных сил на сохранение энергии в системе весьма значительно. Консервативные силы играют важную роль в сохранении энергии, так как позволяют ее преобразовывать из одной формы в другую. Неконсервативные силы, напротив, могут приводить к потере энергии в системе, в результате чего механическая энергия может быть потеряна или превращена в другую форму.
Понимание разницы между консервативными и неконсервативными силами позволяет более точно анализировать и предсказывать изменения энергии в системе и понимать, какие силы и взаимодействия влияют на сохранение энергии.
Потери энергии в механических системах и их компенсация
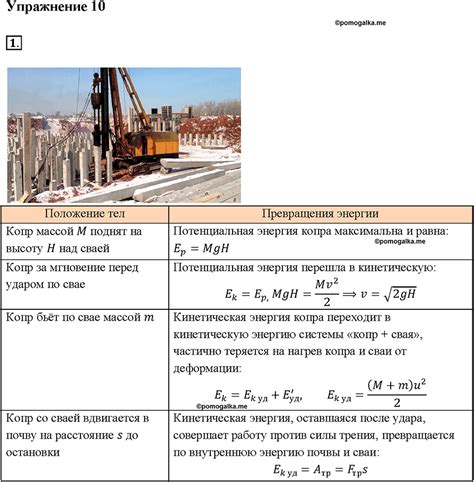
В механических системах неизбежно возникают потери энергии в результате трения, неидеальности механизмов, сопротивления воздуха и других факторов. Однако, согласно закону сохранения энергии, эта потеря энергии должна быть компенсирована другими видами энергии в системе.
Потери энергии в механических системах приводят к постепенному снижению полезной работы, и с целью максимальной эффективности системы необходимо учитывать их в процессе проектирования и эксплуатации.
Одним из способов компенсации потерь энергии является использование механизмов с меньшим трением, что позволяет уменьшить потери энергии в результате трения. Также можно использовать специальные системы смазки для снижения трения между деталями механизмов.
Другим способом компенсации потерь энергии является применение энергетических аккумуляторов или обратных электромеханических систем. Энергия, выделяемая в процессе потерь, может быть сохранена и использована для выполнения работы в моменты, когда потребность в энергии возрастает.
В некоторых случаях возможно использование специальных устройств, таких как подшипники с малым трением, повышающих эффективность системы и уменьшающих потери энергии.
Компенсация потерь энергии в механических системах не только позволяет повысить эффективность, но и увеличить срок службы системы, а также снизить понадобление во внешних источниках энергии.
| Трение | Смазка | Аккумуляторы | Специальные устройства |
|---|---|---|---|
| Одной из основных причин потерь энергии в механических системах является трение между деталями механизмов. Оптимизация формы и материала используемых деталей позволяет уменьшить трение и тем самым снизить потери энергии. | Применение смазок между поверхностями контакта позволяет снизить коэффициент трения и тем самым уменьшить потери энергии. | Использование энергетических аккумуляторов позволяет сохранять и использовать избыточную энергию, выделяемую в процессе потерь, для покрытия временных пиков нагрузки. | Применение специальных устройств, таких как подшипники с малым трением, способствует увеличению эффективности механической системы и снижению потерь энергии. |
Потенциальная энергия и ее связь с силами упругости и гравитации

Сила упругости возникает в результате деформации материала и обусловлена его упругими свойствами. Когда материал деформируется, он имеет потенциальную энергию, которая связана с его упругостью. Потенциальная энергия упругости обратно пропорциональна величине деформации и может быть выражена соотношением:
E = 0.5 k x^2,
где E - потенциальная энергия, k - коэффициент жесткости, x - величина деформации.
Сила гравитации возникает взаимодействием массы двух тел и направлена вдоль линии их центров. Потенциальная энергия, связанная с гравитацией, определяется высотой объекта над определенным уровнем и может быть выражена следующим образом:
E = m g h,
где E - потенциальная энергия, m - масса объекта, g - ускорение свободного падения, h - высота над определенным уровнем.
Таким образом, в механике мы имеем два основных вида потенциальной энергии: потенциальную энергию упругости и потенциальную энергию, связанную с силой гравитации. Объединение этих двух форм потенциальной энергии позволяет анализировать различные физические явления, такие как движение пружины или падение тела под действием гравитации. Понимание этих концепций является важным для понимания основ закона сохранения энергии в механике.
Колебания и их энергетический аспект
Энергетический аспект колебаний связан с законом сохранения энергии, который утверждает, что полная механическая энергия системы остается постоянной во время колебаний. Полная механическая энергия состоит из кинетической и потенциальной энергии.
Кинетическая энергия связана с движением материальной точки или системы частиц и определяется формулой: К = (m*v^2)/2, где m - масса, v - скорость.
Потенциальная энергия связана с положением материальной точки или системы частиц относительно определенного положения и определяется формулой: П = m*g*h, где g - ускорение свободного падения, h - высота.
В процессе колебаний энергия переходит между кинетической и потенциальной формами, но их сумма остается неизменной. Например, при движении маятника энергия переходит от кинетической (максимальной в нижней точке) к потенциальной (максимальной в высшей точке) и обратно.
С помощью закона сохранения энергии можно анализировать различные свойства колебательных систем и проводить расчеты, например, определять период колебаний, амплитуду и максимальную скорость. Также этот закон является основой для понимания различных физических явлений, связанных с колебаниями, таких как звуковые и световые волны, электромагнитные колебания и многие другие.
Механическая работа и ее взаимосвязь с энергией

Работа, совершаемая на телом, может быть использована для изменения его энергии. В механике существует понятие кинетической энергии, которая определяется как энергия движения тела. Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.
Согласно закону сохранения энергии, энергия не может появиться или исчезнуть, она может только изменяться. Таким образом, работа, совершенная над телом, превращается в его кинетическую энергию.
Примеры применения закона сохранения энергии в практических задачах
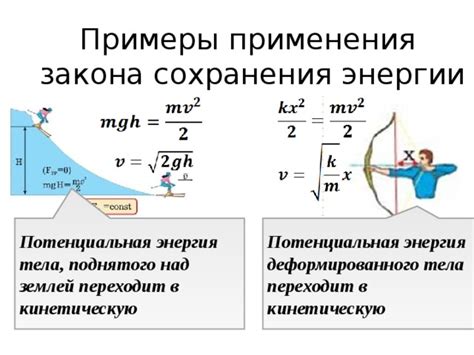
1. Колебания маятника.
Закон сохранения энергии применяется для анализа колебаний маятника. В маятнике механическая энергия переходит из потенциальной в кинетическую и обратно. Начальная потенциальная энергия при отклонении маятника превращается в кинетическую энергию, когда маятник проходит нижнюю точку своего движения. Затем, на максимальном отклонении, вся кинетическая энергия превращается обратно в потенциальную. Таким образом, сумма потенциальной и кинетической энергии остается постоянной на протяжении всего движения маятника.
2. Движение тела, брошенного вертикально вверх.
При броске тела вертикально вверх закон сохранения энергии позволяет рассчитать максимальную высоту подъема тела. На высоте подъема кинетическая энергия тела полностью превратится в потенциальную энергию, равную работе силы тяжести при подъеме. С учетом потерь энергии на сопротивление воздуха или трение, можно определить, на какой высоте тело остановится.
3. Свободное падение тела.
Закон сохранения энергии также применяется для анализа свободного падения тела. При падении тело приобретает кинетическую энергию, которая в дальнейшем полностью превращается в потенциальную энергию при достижении максимальной высоты подъема. Таким образом, сумма кинетической и потенциальной энергии остается постоянной на протяжении всего падения.
4. Работа силы упругости.
При растяжении или сжатии упругого материала, закон сохранения энергии позволяет рассчитать работу силы упругости. Потенциальная энергия упругой деформации сохраняется, и при восстановлении исходной формы тела, эта энергия превращается в кинетическую. Таким образом, работа силы упругости равна изменению потенциальной энергии тела.
Закон сохранения энергии в механике позволяет более полно и точно анализировать различные физические процессы и решать практические задачи в области механики.



