Характеристическое уравнение – это математическое выражение, которое связывает коэффициенты дифференциального уравнения с его решениями. Оно позволяет найти собственные значения и собственные функции, которые определяют форму частного решения дифференциального уравнения.
Дифференциальное уравнение – это уравнение, связывающее функцию или неизвестную переменную с ее производной. Чтобы найти общее решение дифференциального уравнения, необходимо найти все его частные решения. Одним из способов решения является метод нахождения характеристического уравнения.
Характеристическое уравнение получается путем замены функции в дифференциальном уравнении на экспоненциальную функцию, и решение этого уравнения дает значения параметров, при которых дифференциальное уравнение имеет нетривиальные решения. Собственные значения и собственные функции, полученные из характеристического уравнения, играют ключевую роль в решении дифференциальных уравнений и имеют физическую интерпретацию в различных областях науки.
Определение характеристического уравнения
Характеристическое уравнение выражает связь между коэффициентами и производными искомой функции. Оно получается путем замены производной искомой функции в исходном дифференциальном уравнении на соответствующую степень ее переменной и решения полученного алгебраического уравнения.
Характеристическое уравнение может иметь различные виды в зависимости от типа дифференциального уравнения и его порядка. Например, для линейного дифференциального уравнения второго порядка характеристическое уравнение представляет собой квадратное уравнение, которое можно решить с помощью стандартных методов.
| Тип дифференциального уравнения | Характеристическое уравнение |
|---|---|
| Линейное уравнение первого порядка | ax + b = 0 |
| Линейное уравнение второго порядка | ax^2 + bx + c = 0 |
| Уравнение с постоянными коэффициентами | a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0 = 0 |
Решение характеристического уравнения позволяет определить вид общего решения дифференциального уравнения. Далее, используя начальные условия или граничные условия, можно найти конкретное решение дифференциального уравнения.
Области применения характеристического уравнения

Одной из основных областей, где используется характеристическое уравнение, является теория управления и регулирования. Характеристическое уравнение позволяет определить устойчивость системы управления и предсказать ее поведение в зависимости от входных сигналов. Это позволяет инженерам и научным исследователям разрабатывать оптимальные регулировочные системы, а также анализировать и оптимизировать уже существующие системы управления.
В области электротехники и электроники характеристическое уравнение используется для анализа и проектирования различных электрических и электронных систем. Например, оно позволяет определить частотные характеристики фильтров, устойчивость электрических цепей и систем передачи данных.
Характеристическое уравнение также находит свое применение в механике и аэродинамике для анализа и оптимизации движения твердого тела и аэродинамических систем, таких как самолеты и автомобили. Оно позволяет определить устойчивость и колебательные характеристики системы, а также предсказать ее поведение в различных условиях.
Кроме того, характеристическое уравнение используется в физике, медицине, экономике и других научных и прикладных областях. Оно помогает исследователям и специалистам анализировать и моделировать различные технические и физические процессы, предсказывать их развитие и принимать обоснованные решения на основе полученных результатов.
Таким образом, характеристическое уравнение является мощным инструментом, который находит применение во многих областях науки и техники. Оно позволяет анализировать и оптимизировать различные системы, предсказывать их поведение и принимать обоснованные решения на основе полученных результатов.
Связь характеристического уравнения с дифференциальным уравнением
Дифференциальное уравнение – это уравнение, содержащее производные неизвестной функции. Для решения дифференциального уравнения необходимо найти такую функцию, которая при подстановке в данное уравнение удовлетворяет ему при любых значениях аргумента.
Характеристическое уравнение получается путем замены производных искомой функции в дифференциальном уравнении на символы. Таким образом, получается уравнение, содержащее только символы и производные порядка n. После решения характеристического уравнения получаются корни - значения символов, которые затем используются для нахождения общего решения дифференциального уравнения.
Характеристическое уравнение может иметь разные виды в зависимости от типа дифференциального уравнения. Например, для линейных дифференциальных уравнений порядка n, характеристическое уравнение будет иметь вид anrn + an-1rn-1 + ... + a1r + a0 = 0, где an, an-1, ..., a1, a0 - коэффициенты дифференциального уравнения, r - символ.
Таким образом, характеристическое уравнение связывает значения символов с решениями дифференциального уравнения, позволяя определить вид и структуру общего решения.
Как решить характеристическое уравнение

Для решения характеристического уравнения необходимо выполнить следующие шаги:
- Записать линейное дифференциальное уравнение в стандартной форме, выделив коэффициенты при производных и при функции.
- Найти характеристическое уравнение, заменив производные на характеристические значения.
- Решить характеристическое уравнение, найдя все его корни.
- Используя корни характеристического уравнения, составить общее решение линейного дифференциального уравнения.
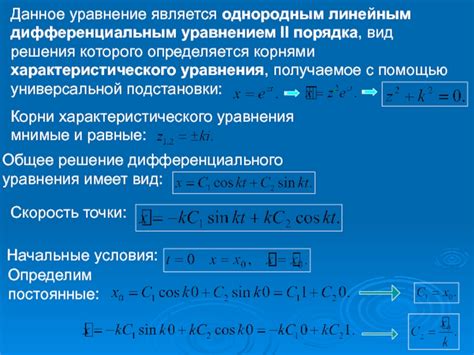
Решение характеристического уравнения может давать действительные или комплексные корни. Если корень характеристического уравнения имеет кратность больше 1, то соответствующая функция в общем решении будет иметь вид t^k * e^(r*t), где k - кратность корня, t - независимая переменная, e - основание натурального логарифма, r - вещественная или комплексная составляющая корня.
Таким образом, решение характеристического уравнения позволяет получить полное описание поведения функций, удовлетворяющих линейному дифференциальному уравнению. Это позволяет проводить анализ и прогнозирование различных процессов и явлений, в которых присутствуют линейные дифференциальные уравнения.
Роль корней характеристического уравнения в решении дифференциального уравнения

Корни характеристического уравнения отражают свойства системы, описываемой дифференциальным уравнением. Величина их кратности определяет структуру общего решения и характер движения системы.
Если корни характеристического уравнения являются действительными и различными, то общее решение дифференциального уравнения можно представить в виде суммы общих решений, соответствующих каждому корню. В этом случае система имеет линейно независимые решения, а поведение системы определяется экспоненциальным убыванием или ростом с течением времени.
Если корни характеристического уравнения повторяются, то общее решение содержит члены, множители которых являются степенями времени. В этом случае система имеет кратные решения, что свидетельствует о наличии в системе гармонического движения с определенной частотой.
| Тип корней характеристического уравнения | Структура общего решения | Поведение системы во времени |
|---|---|---|
| Действительные и различные | Сумма экспоненциальных функций | Экспоненциальное убывание или рост |
| Действительные и совпадающие | Линейная комбинация экспоненциальных функций и степеней времени | Гармоническое движение |
Таким образом, понимание роли корней характеристического уравнения позволяет определить основные свойства решения дифференциального уравнения и описать поведение системы во времени. Это является важным инструментом в анализе и решении широкого класса дифференциальных уравнений.
Примеры применения характеристического уравнения в физике

Пример 1: Гармонические колебания
Одним из примеров применения характеристического уравнения является анализ гармонических колебаний. Для системы, описывающей колебания, характеристическое уравнение можно получить путем решения дифференциального уравнения, описывающего движение системы. Решение характеристического уравнения позволяет определить собственные частоты колебаний и их характер (резонанс, затухание и т. д.).
Пример 2: Электромагнитные волны
При изучении электромагнитных волн также можно использовать характеристическое уравнение. Например, для определения распространяющихся волн в параллельных проводах в теории электрических цепей применяется характеристическое уравнение, которое позволяет найти параметры волнового процесса, такие как скорость распространения волн и их амплитуда.
Пример 3: Колебательные системы
Характеристическое уравнение также находит применение при изучении колебательных систем, состоящих из связанных масс и пружин. Оно позволяет определить собственные частоты колебаний системы, а также связанные с этими частотами амплитуды и фазы колебаний.
Характеристическое уравнение является мощным инструментом в физике, который позволяет анализировать различные физические процессы. Оно применяется при изучении гармонических колебаний, электромагнитных волн и колебательных систем. Знание характеристического уравнения позволяет более глубоко понять эти явления и проводить расчеты и эксперименты с большей точностью.
Связь между корнями характеристического уравнения и поведением решений дифференциального уравнения
Если все корни характеристического уравнения являются вещественными и отличными друг от друга, то решение дифференциального уравнения будет содержать экспоненциальные функции вида emx, где m - корень характеристического уравнения. В этом случае решение будет иметь вид:
- если корень положительный, то решение будет экспоненциально растущим с ростом x;
- если корень отрицательный, то решение будет экспоненциально убывающим с ростом x;
Если корни характеристического уравнения являются комплексными с ненулевой мнимой частью, то решение дифференциального уравнения будет содержать синусоидальные функции вида Aeαxsin(βx + φ), где A - амплитуда, α - коэффициент демпфирования, β - частота собственных колебаний, φ - начальная фаза. В этом случае решение будет иметь вид:
если коэффициент демпфирования меньше нуля, то решение будет осциллировать с убывающей амплитудой;
если коэффициент демпфирования равен нулю, то решение будет сохранять постоянную амплитуду;
если коэффициент демпфирования больше нуля, то решение будет затухающим колебанием.
Таким образом, связь между корнями характеристического уравнения и поведением решений дифференциального уравнения позволяет предсказывать динамику систем, описываемых дифференциальными уравнениями. Данное знание играет важную роль в различных областях науки и техники, где дифференциальные уравнения используются для моделирования и анализа различных процессов и явлений.
Общая формула для характеристического уравнения в зависимости от типа дифференциального уравнения

Для линейного однородного дифференциального уравнения порядка n, имеющего вид:
an(x)y(n)(x) + an-1(x)y(n-1)(x) + ... + a1(x)y'(x) + a0(x)y(x) = 0,
где y(k)(x) обозначает k-ую производную функции y(x), коэффициенты ai(x) являются функциями независимой переменной x, общая формула для характеристического уравнения имеет вид:
an(x)rn + an-1(x)rn-1 + ... + a1(x)r + a0(x) = 0.
Для линейного однородного дифференциального уравнения второго порядка, имеющего вид:
a(x)y''(x) + b(x)y'(x) + c(x)y(x) = 0,
где y''(x) обозначает вторую производную функции y(x), коэффициенты a(x), b(x) и c(x) являются функциями независимой переменной x, общая формула для характеристического уравнения имеет вид:
a(x)r2 + b(x)r + c(x) = 0.
Эти формулы позволяют определить значения r, которые будут корнями характеристического уравнения. Зная корни характеристического уравнения, можно найти решение дифференциального уравнения в зависимости от типа и начальных условий.



