Анализ и решение задач, связанных с точками пересечения, являются важной частью математики и графического анализа. Эти задачи могут быть применены в различных областях, от архитектуры и инженерии до экономики и физики. Понимание условий принадлежности точек пересечения играет важную роль в решении таких задач.
При анализе точек пересечения необходимо учитывать различные факторы, такие как графическое представление объекта или системы, уравнения, определения и граничные условия. Зная эти факторы, можно провести анализ и определить, какие точки являются пересечениями, а какие нет.
Одним из важных аспектов анализа точек пересечения является использование логических операций и математических методов. Дополнительные математические инструменты, такие как уравнения, системы уравнений, графики и геометрические формулы, могут быть использованы для более точного анализа и решения задач.
Чтобы успешно решать задачи, связанные с точками пересечения, необходимо иметь навыки анализа, логического мышления и умение применять математические методы. На практике, исследование и решение задач точек пересечения может помочь нам в понимании взаимосвязи различных факторов и осуществлении эффективного управления и принятия решений.
Что определяет условие принадлежности точек пересечения?
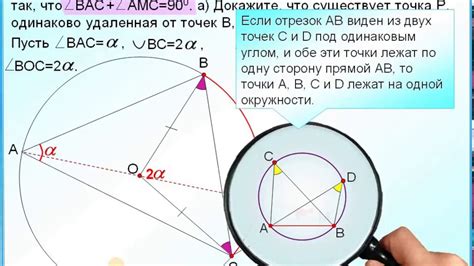
Условие принадлежности точек пересечения определяет, находятся ли данные точки на одной или разных кривых, отрезках или плоскостях. Чтобы понять, принадлежат ли точки пересечения к одной фигуре или объекту, необходимо выполнить анализ соответствующих уравнений и установить, удовлетворяют ли они условиям для обеих кривых или отрезков.
Одно из наиболее распространенных условий для принадлежности точек пересечения - существование уравнений, которым эти точки удовлетворяют. Например, для двух кривых, пересекающихся в одной точке, координаты этой точки должны удовлетворять уравнениям обеих кривых.
В некоторых случаях условие принадлежности может быть представлено в виде системы уравнений. Решив эту систему, можно определить, удовлетворяют ли точки пересечения условиям принадлежности к объектам.
Также условие принадлежности может зависеть от свойств и характеристик объектов или кривых, которые пересекаются. Например, для определения принадлежности точек пересечения графикам функции круг или прямоугольник может использоваться геометрическое условие: точка пересечения должна находиться внутри пределов круга или прямоугольника.
Необходимость учета всех условий принадлежности точек пересечения позволяет более точно анализировать и решать задачи, связанные с пересечением графиков, плоскостей, отрезков и других геометрических объектов.
Анализ задач и его роль в определении принадлежности точек пересечения
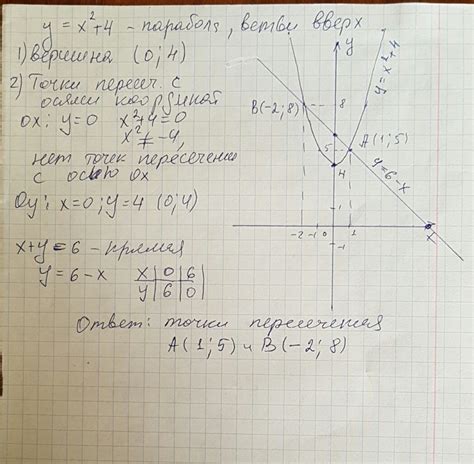
Анализ задачи является первым шагом в процессе решения задачи о принадлежности точек пересечения. Важно понять, какие данные предоставлены в условии задачи и что требуется найти. На основе этого можно определить, какой подход или метод решения будет наиболее эффективным.
Основная цель анализа задачи - выделить ключевые элементы, которые позволят определить, принадлежат ли точки пересечения заданным условиям или нет. Например, в задаче может быть дано уравнение прямой и кривой, и нужно найти их точки пересечения. В таком случае ключевыми элементами будут коэффициенты уравнений, и решением задачи будет нахождение значений переменных, при которых уравнения выполняются одновременно.
Анализ задачи также позволяет определить ограничения и предположения, которые могут быть применены при решении. Например, в задаче может быть указано, что точки пересечения не должны превышать определенные значения координат или должны принадлежать определенной области. Зная такие ограничения, можно более эффективно решить задачу и получить более точные результаты.
Кроме того, анализ задачи помогает определить алгоритм действий, который необходимо выполнить для решения задачи. Например, если в задаче требуется найти точки пересечения с помощью графического метода, то анализ задачи позволит установить, какие шаги нужно предпринять для построения графиков и найдения точек пересечения.
Таким образом, анализ задачи играет важную роль в определении принадлежности точек пересечения. Он позволяет выделить ключевые элементы задачи, определить ограничения и выбрать правильный метод решения. Без анализа задачи решение может быть неполным или неправильным, поэтому этот этап необходим для достижения точных и корректных результатов.
Решение задач о принадлежности точек пересечения: методы и приемы
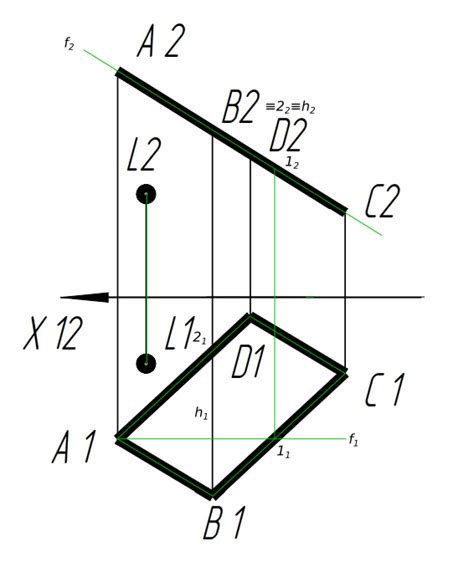
Один из самых популярных методов - использование алгоритма положения точки относительно прямой. Этот метод позволяет определить, находится ли точка внутри фигуры или снаружи, основываясь на ее координатах и уравнении прямой, которую можно получить из уравнения границ фигуры.
| Метод | Описание | Применение |
|---|---|---|
| Алгоритм положения точки относительно прямой | Определяет, находится ли точка с одной стороны прямой или нет | Для определения принадлежности точек пересечения фигурам |
| Анализ системы уравнений | Решает систему уравнений с двумя неизвестными | Позволяет найти точку пересечения двух прямых или границ фигур |
| Метод исключения | Исключает одну из неизвестных, чтобы найти значение другой неизвестной | Применяется для нахождения координаты точки пересечения двух прямых или границ фигур |
Naстоящий анализ и решение задач о принадлежности точек пересечения требуют же использования комбинации методов и приемов, чтобы получить точные результаты. В некоторых задачах также может понадобиться использование методов геометрического построения, нахождения площадей фигур или других специфических приемов.
Важно учитывать, что решение задач о принадлежности точек пересечения должно быть основано на четком понимании геометрических принципов и правил. Правильное применение методов и приемов позволяет получить достоверный результат и избежать ошибок в решении задач.
Графический анализ и его значимость в определении принадлежности точек пересечения
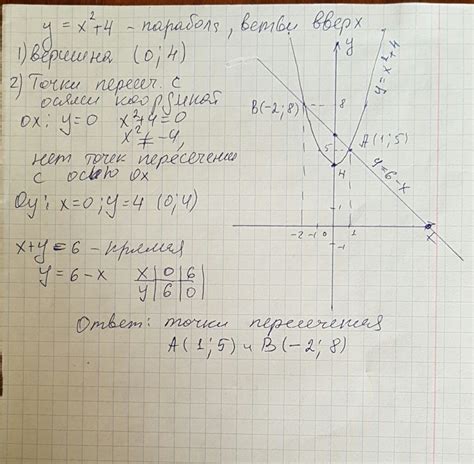
Основной шаг графического анализа заключается в построении графиков функций. При их пересечении мы можем наблюдать точки, в которых обе функции принимают одинаковые значения. Эти точки являются решениями системы уравнений и показывают места, где графики пересекаются.
Графический анализ также позволяет определить количество точек пересечения и их природу. Если две функции пересекаются в единственной точке, то это означает, что система имеет одно решение. В случае, когда графики функций совпадают полностью, система имеет бесконечное количество решений. Если графики не пересекаются вообще, то система не имеет решений.
Алгебраический анализ и его влияние на определение принадлежности точек пересечения
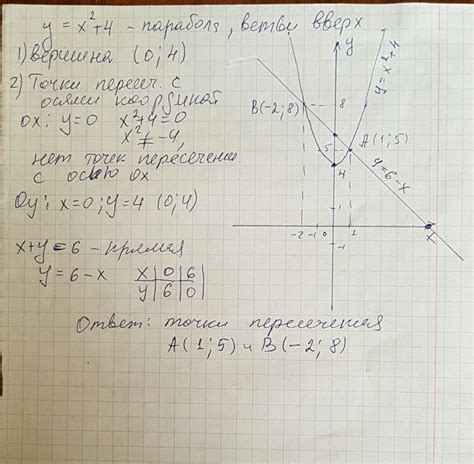
Алгебраический анализ позволяет решать задачи, связанные с нахождением корней уравнений. Корень уравнения - это значение переменной, при котором уравнение принимает нулевое значение. Для многочленов, которые являются одним из наиболее распространенных типов алгебраических объектов, задача нахождения корней может быть решена методами алгебраического анализа.
Одним из основных методов алгебраического анализа, используемых для определения принадлежности точек пересечения, является метод подстановки. Этот метод заключается в том, чтобы заменить переменные в уравнениях на известные значения и проверить, удовлетворяют ли эти значения самим уравнениям. Если уравнения выполняются при подстановке конкретного значения переменной, то точка пересечения будет принадлежать этому уравнению.
Также для определения принадлежности точек пересечения используется метод графического представления. Графический анализ позволяет наглядно увидеть, где находятся точки пересечения и определить их принадлежность уравнениям. Для этого необходимо построить графики уравнений и найти точки их пересечения. Если точка находится на графике уравнения, то она принадлежит этому уравнению.
Таким образом, алгебраический анализ играет важную роль в определении принадлежности точек пересечения и решении задач, связанных с этой темой. Методы алгебраического анализа позволяют точно определить, принадлежат ли точки пересечения заданным уравнениям, и помогают найти решения для таких задач.
Отображение точек пересечения в системе координат и его важность в анализе задач
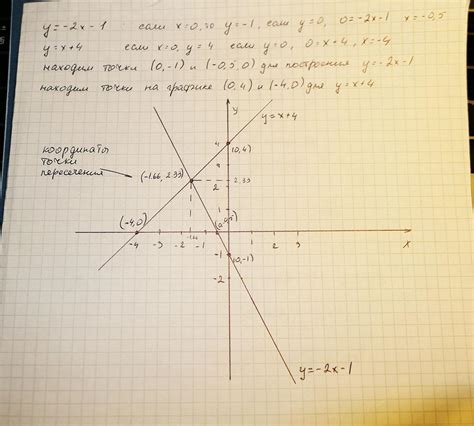
Точки пересечения играют важную роль в анализе задач, связанных с графиками и системами уравнений. Эти точки представляют собой места, где два или более графика пересекаются друг с другом.
Для визуализации и анализа этих точек в системе координат используется график, который позволяет наглядно представить связь между переменными и их значениями.
График строится на плоскости, где по горизонтальной оси откладываются значения одной переменной, а по вертикальной оси - значения другой переменной. Таким образом, точки пересечения могут быть представлены в виде координат на этой плоскости.
Отображение точек пересечения в системе координат имеет ряд практических применений:
- Определение решения системы уравнений. Если система уравнений имеет решение, то точки пересечения графиков уравнений на плоскости будут искомым решением системы.
- Анализ графиков функций. Точки пересечения графиков функций могут указывать на значения, в которых функции равны друг другу или на местах возникновения особых точек, таких как минимумы или максимумы функции.
- Построение графиков для визуализации данных. Отображая точки пересечения на графике, можно наглядно представить полученные результаты и особенности исследуемых данных.
Таким образом, отображение точек пересечения в системе координат играет важную роль в анализе и решении задач, связанных с графиками и системами уравнений. Позволяя визуализировать и анализировать данные, оно помогает более глубоко понять характеристики и связи между переменными.
Ограничения и осложнения при определении принадлежности точек пересечения
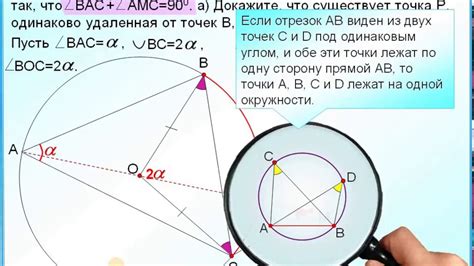
Определение принадлежности точек пересечения может оказаться сложной задачей, требующей внимательного анализа и решения. Существуют ряд ограничений и осложнений, которые могут возникнуть при решении таких задач.
Во-первых, необходимо учитывать ограничения, налагаемые условиями задачи. Иногда точки пересечения могут быть ограничены в пространстве или времени, что требует более тщательного анализа и поиска решения.
Во-вторых, нельзя забывать о возможных осложнениях, связанных с точностью и достоверностью исходных данных. Погрешности измерений или неполная информация могут существенно влиять на результаты определения принадлежности точек пересечения.
Кроме того, необходимо учитывать сложность математических моделей или алгоритмов, используемых для определения точек пересечения. Некоторые модели требуют высокой вычислительной мощности или специального программного обеспечения, что добавляет дополнительные осложнения в процесс анализа и решения задач.
Не менее важным фактором является понимание контекста и целей задачи. Определение принадлежности точек пересечения может иметь разные трактовки в зависимости от задачи, поэтому необходимо учесть все факторы при анализе и решении.
В целом, определение принадлежности точек пересечения – это комплексная задача, требующая не только математических вычислений, но и глубокого понимания условий и ограничений задачи. Только при учете всех факторов можно достичь точности и достоверности результата.



