Тригонометрия – это ветвь математики, которая изучает связи между углами и сторонами треугольников. Одной из самых важных тригонометрических функций является косинус. Косинус угла равен отношению длины прилегающего катета к гипотенузе прямоугольного треугольника.
Углы, измеренные в градусах, являются наиболее распространенным способом измерения углов. Существует 360 градусов в одном полном обороте, и тригонометрические функции могут быть вычислены для любого угла в диапазоне от 0 до 360 градусов. Один из таких углов - 135 градусов.
Таким образом, чтобы найти косинус 135 градусов, нужно рассмотреть прямоугольный треугольник с углом в 135 градусов и найти отношение длины прилегающего катета к гипотенузе.
Косинус 135 градусов: значение, свойства и применение
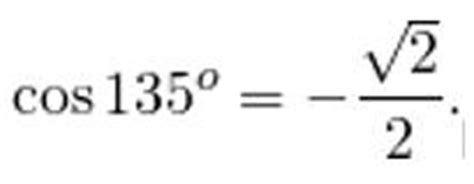
Косинус 135 градусов - это математическая функция, которая выражает отношение длины прилегающего катета к длине гипотенузы в прямоугольном треугольнике с углом 135 градусов.
Значение косинуса 135 градусов равно -0.707.
Косинус является периодической функцией, период которой равен 360 градусов или 2π радиан. Значение косинуса может варьироваться от -1 до 1, в зависимости от угла.
Косинус угла 135 градусов имеет ряд свойств, которые являются следствием его определения. Некоторые из них:
| Угол (градусы) | Косинус |
|---|---|
| 30 | 0.866 |
| 45 | 0.707 |
| 60 | 0.5 |
| 90 | 0 |
| 135 | -0.707 |
| 180 | -1 |
| 270 | 0 |
| 360 | 1 |
Основные области применения косинуса включают геометрию, физику, инженерные и технические науки. Косинус используется для решения уравнений, нахождения расстояний, а также в области синусоидальных колебаний и волновой оптики.
Тригонометрические функции и их значение в математике
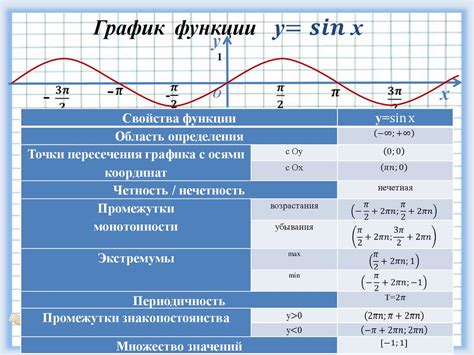
Одной из основных тригонометрических функций является косинус. Косинус угла в определенном треугольнике равен отношению длины прилегающего катета к гипотенузе. Однако, косинус может принимать значения не только в пределах треугольника, но и вне его, и это уже абстрактное понятие, различное от традиционной геометрии.
Таким образом, косинус 135 градусов приближенно равен -0.707, что подтверждает его отрицательное значение. Значение косинуса 135 градусов может использоваться в дальнейших математических расчетах, например, при решении задач в физике или астрономии.
Угол 135 градусов: определение и особенности
Для определения косинуса данного угла важно знать его принадлежность к четвертой четверти координатной плоскости. В этой четверти косинус угла положителен, так как x-координата находится в отрицательном диапазоне, а y-координата - в положительном диапазоне.
Таким образом, косинус 135 градусов равен отрицательной величине, близкой к нулю.
| Угол | Косинус |
|---|---|
| 135 градусов | -0.7071 |
Исключительно важно отметить, что значение косинуса угла 135 градусов может быть использовано в различных областях науки и техники, таких как физика, инженерия и компьютерная графика.
Косинус: определение и свойства
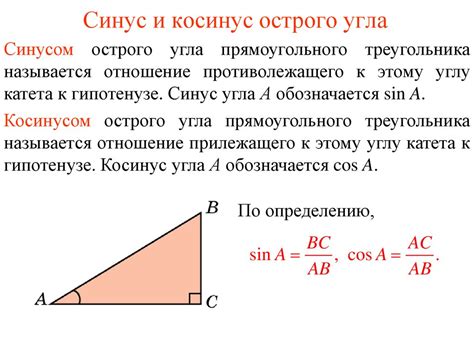
Косинус градуса рассчитывается с помощью формулы:
cos(α) = adjacent/hypotenuse
Где:
- cos - функция косинуса;
- α - значение угла, измеренное в радианах или градусах;
- adjacent - длина прилежащего катета;
- hypotenuse - длина гипотенузы.
Из определения косинуса следует несколько важных свойств:
- Косинус угла равен отношению длины прилежащего катета к длине гипотенузы.
- Значение косинуса всегда находится в диапазоне от -1 до 1.
- Косинус угла 0 равен 1.
- Косинус угла 90 градусов равен 0.
- Косинус для угла 180 градусов равен -1.
- Косинусы сопряженных углов или углов, сумма которых составляет 180 градусов, равны друг другу величиной, но имеют разные знаки.
Таким образом, зная значения косинусов для различных углов, можно решать разнообразные математические и физические задачи, связанные с прямоугольными треугольниками, колебаниями, осцилляциями, векторами и другими явлениями.
Как найти косинус 135 градусов: формула и вычисления
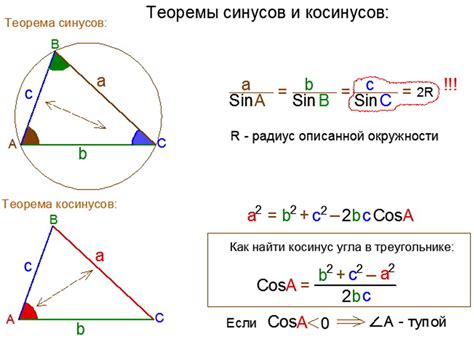
Для нахождения косинуса 135 градусов используется следующая формула:
cos(135°) = cos(180° - 135°) = cos(45°)
Для градусов, которые лежат в третьем квадранте (больше 90 и меньше 180), косинус может быть рассчитан путем нахождения значения соответствующего угла в первом квадранте (180 минус заданный угол).
Таким образом, угол 135 градусов может быть преобразован в эквивалентный угол в первом квадранте, который равен 45 градусам. Поскольку косинус 45 градусов уже известен, мы можем использовать его значение для вычисления косинуса 135 градусов.
В итоге получаем:
cos(135°) = cos(45°) = √2 / 2 ≈ 0.7071
Таким образом, косинус 135 градусов равен приблизительно 0.7071.
Косинус 135 градусов: значение и примеры
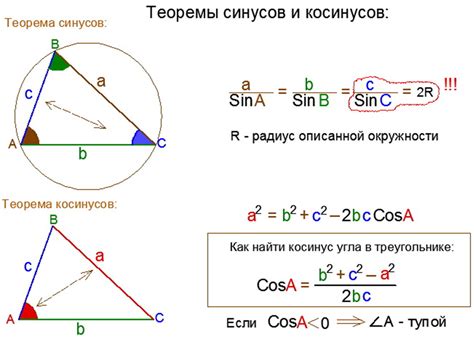
Косинус угла измеряет отношение прилежащей стороны прямоугольного треугольника к его гипотенузе. Значение косинуса 135 градусов можно рассчитать по следующей формуле:
cos(135°) = cos(180° - 135°)
cos(135°) = -cos(45°)
Зная, что косинус 45 градусов равен √2 / 2, получаем:
cos(135°) = -√2 / 2
Таким образом, косинус 135 градусов равен -√2 / 2.
Рассмотрим некоторые примеры, демонстрирующие применение значения косинуса 135 градусов:
- Если угол между двумя векторами равен 135 градусам, то косинус этого угла будет равен -√2 / 2. Это позволяет определить, насколько сонаправлены или противоположно направлены векторы.
- При решении задач геометрии или физики, где требуется вычислить отношение прилежащей стороны прямоугольного треугольника к его гипотенузе, можно использовать значение косинуса 135 градусов.
- В компьютерной графике, косинус 135 градусов может использоваться для вычисления позиции точки при заданном радиусе и угле поворота.
Применение косинуса 135 градусов в реальной жизни

- Архитектура: Косинус 135 градусов может использоваться при расчете угла наклона крыши здания или при определении угла между сторонами прямоугольных строений.
- Авиация: Косинус 135 градусов может помочь в определении угла взлета и посадки самолета, а также при расчете траектории полета.
- Машиностроение: При проектировании механизмов и машин косинус 135 градусов может применяться для расчета геометрических параметров и угловых соединений.
- Графика и дизайн: Косинус 135 градусов может быть использован при создании трехмерных моделей и анимации для определения углов поворота объектов.
- Физика: В некоторых физических задачах использование косинуса 135 градусов может помочь в определении направления силы или вектора.



