Существует множество систем счисления, которые используются в различных областях науки и техники. Два из них – восьмеричная и шестнадцатеричная – имеют особую важность и применяются в программировании, при работе с компьютерами и электроникой в целом. Они отличаются от привычной десятичной системы и имеют особенности, свойственные только им.
Восьмеричная система счисления основана на использовании восьми различных символов – цифр от 0 до 7. Числа в этой системе записываются с помощью этих цифр, а каждая позиция числа имеет свой вес. Например, число 56 в восьмеричной системе равно 5*8 + 6 = 46 в десятичной системе.
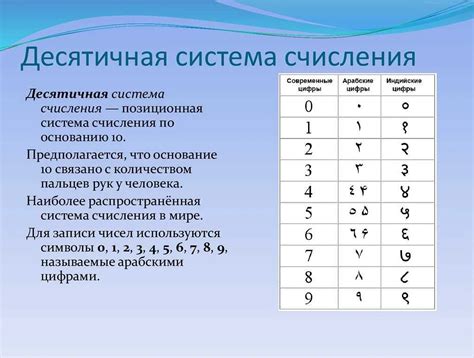
Шестнадцатеричная система счисления использует шестнадцать различных символов – цифры от 0 до 9 и буквы от A до F. Позиционное обозначение в этой системе также имеет свой вес. Например, число AC в шестнадцатеричной системе равно 10*16 + 12 = 172 в десятичной системе.
Различные приложения требуют использования восьмеричной и шестнадцатеричной систем счисления. Они нашли свое применение в программировании, поскольку удобны для представления двоичного кода, а также для работ с памятью компьютера и его регистрами. Знание этих систем позволяет разработчикам эффективно оперировать данными и легче понять их внутреннюю структуру.
Восьмая с точкой и шестнадцатая чему равна
Восьмеричная система счисления базируется на числе 8 и использует восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Восьмеричное число представляется в виде последовательности цифр, где каждая цифра умножается на соответствующую степень числа 8. Например, число 125 в восьмеричной системе счисления будет представляться как 175, так как 1 * 8^2 + 7 * 8^1 + 5 * 8^0 = 125.
Шестнадцатеричная система счисления базируется на числе 16 и использует шестнадцать цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. При этом буквы от A до F обозначают числа от 10 до 15 соответственно. Шестнадцатеричное число также представляется в виде последовательности цифр, где каждая цифра умножается на соответствующую степень числа 16. Например, число AB в шестнадцатеричной системе счисления будет представляться как 171, так как A * 16^1 + B * 16^0 = 10 * 16^1 + 11 * 16^0 = 160 + 11 = 171.
Восьмеричная и шестнадцатеричная системы счисления широко используются в программировании и компьютерных системах для представления чисел и данных, так как они позволяют компактно хранить и обрабатывать большие числа и битовые последовательности.
Расчёт восьмиричной и шестнадцатиричной систем счисления

В восьмиричной системе счисления используются цифры от 0 до 7. Порядок цифр в числе определяет их взаимосвязь и значимость. Например, число 358 читается как "три пять в восьмеричной системе". Расчет числа в восьмиричной системе осуществляется следующим образом:
358 = 3 * 81 + 5 * 80 = 24 + 5 = 2910
То есть число 358 в десятичной системе равно 29.
В шестнадцатиричной системе счисления используются цифры от 0 до 9 и буквы A, B, C, D, E, F, которым соответствуют значения от 10 до 15. Порядок цифр и букв также определяет их взаимосвязь и значимость. Например, число 2F16 читается как "два эф в шестнадцатеричной системе". Расчет числа в шестнадцатеричной системе осуществляется аналогично:
2F16 = 2 * 161 + 15 * 160 = 32 + 15 = 4710
То есть число 2F16 в десятичной системе равно 47.
Расчет и использование восьмиричной и шестнадцатиричной систем счисления широко применяются в программировании, компьютерных системах и дискретной математике.
Значение восьмиричной и шестнадцатиричной систем счисления

Восьмеричная система счисления, также известная как октальная система, основана на числе 8. В этой системе используются цифры от 0 до 7. Каждая цифра в восьмеричной системе представляет собой степень числа 8.
Например, число 25 в восьмеричной системе будет представлено как 31, так как 3 × 8^1 + 1 × 8^0 = 25.
Шестнадцатиричная система счисления, или гексадецимальная система, основана на числе 16. В этой системе используются цифры от 0 до 9 и буквы от A до F, которые представляют значения от 10 до 15. Каждая цифра в шестнадцатеричной системе также представляет собой степень числа 16.
Например, число 42 в шестнадцатеричной системе будет представлено как 2A, так как 2 × 16^1 + 10 × 16^0 = 42.
Восьмеричная и шестнадцатеричная системы счисления широко применяются в компьютерных науках и программировании, так как позволяют более компактно представить большие числа и упрощают работу с битами и байтами.
Примеры использования восьмиричной и шестнадцатиричной систем счисления

Восьмиричная система счисления (октальная система) основана на использовании восемь цифр: от 0 до 7. Это позволяет представлять числа с использованием меньшего количества символов по сравнению с десятичной системой.
Пример использования восьмиричной системы счисления: представим число 156 в восьмиричной форме. Для этого нужно разбить число на группы по 3 цифры, начиная справа, и записать каждую группу в восьмиричной форме. В результате получим число 234 в восьмиричной системе (156 = 2348).
Шестнадцатиричная система счисления (гексадецимальная система) основана на использовании шестнадцати цифр: от 0 до 9 и от A до F. Это позволяет представлять числа с использованием ещё меньшего количества символов по сравнению с восьмиричной или десятичной системами.
Пример использования шестнадцатиричной системы счисления: представим число 167 в шестнадцатиричной форме. Для этого нужно разбить число на группы по 4 цифры, начиная справа, и записать каждую группу в шестнадцатиричной форме. В результате получим число A7 в шестнадцатиричной системе (167 = A716).
Сравнение восьмиричной и шестнадцатиричной систем счисления

Восьмиричная система счисления использует 8 различных цифр: 0, 1, 2, 3, 4, 5, 6, 7. В то время как шестнадцатиричная система счисления использует 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Цифры A, B, C, D, E, F обозначают значения 10, 11, 12, 13, 14, 15 соответственно.
Основным преимуществом шестнадцатиричной системы счисления является то, что она позволяет представлять большие числа более компактно. Например, число 255 в восьмиричной системе будет представлено как 377, а в шестнадцатиричной системе - FF.
Восьмеричная система счисления часто используется при работе с компьютерами и программировании, так как в них довольно распространены биты и байты, значения которых удобно представлять в восьмиричной системе. Шестнадцатиричная система счисления также широко используется в программировании, так как определенные значения и побитовые операции могут быть представлены более компактно и читабельно.
Таблица ниже показывает эквивалентные значения восьмеричной и шестнадцатеричной систем счисления:
| Десятичное число | Восьмеричное число | Шестнадцатеричное число |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| 7 | 7 | 7 |
| 8 | 10 | 8 |
| 9 | 11 | 9 |
| 10 | 12 | A |
| 11 | 13 | B |
| 12 | 14 | C |
| 13 | 15 | D |
| 14 | 16 | E |
| 15 | 17 | F |
Преимущества использования восьмиричной и шестнадцатиричной систем счисления

Одним из основных преимуществ использования восьмиричной системы счисления является экономия знаков. Восьмеричная система использует только цифры от 0 до 7, что позволяет представить большое число с помощью меньшего количества цифр, чем в десятичной системе. Это особенно полезно при работе с большими числами или при передаче данных, так как можно сократить объем информации.
Шестнадцатиричная система счисления также имеет свои преимущества. Одно из них - легкость чтения и записи. Шестнадцатеричные числа обозначаются с помощью цифр от 0 до 9 и букв от A до F. Буквы используются для представления чисел от 10 до 15, что делает запись чисел более компактной и понятной.
Восьмеричная и шестнадцатиричная системы также часто используются в информатике и программировании. Восьмеричная система часто используется для представления флагов и прав доступа, а шестнадцатеричная система - для представления цветов и адресов памяти. Это обусловлено тем, что восьмеричная и шестнадцатеричная системы позволяют легко работать с битами и байтами, что является важным аспектом в информационных технологиях.
Использование восьмиричной и шестнадцатиричной систем счисления имеет свои преимущества, которые позволяют упростить и улучшить процесс представления чисел и работы с данными. Они позволяют экономить место, облегчают понимание и упрощают процесс работы с битами и байтами. Поэтому знание и использование этих систем счисления является важным для программистов и специалистов в области информационных технологий.
Недостатки использования восьмиичной и шестнадцатиричной систем счисления

Восьмиричная и шестнадцатиричная системы счисления имеют свои преимущества, которые мы рассмотрели в предыдущих разделах. Однако, они также имеют свои недостатки, которые важно учитывать при использовании этих систем.
Недостатки восьмеричной системы счисления:
- Восьмеричная система менее удобна для людей, так как ее основание не является естественным для большинства повседневных задач;
- Перевод чисел из восьмеричной системы в десятичную и наоборот требует дополнительных вычислений и может быть достаточно сложным для неподготовленных людей;
- При использовании восьмеричной системы возникают сложности при работе с большими числами, так как количество символов ограничено до цифр от 0 до 7.
Недостатки шестнадцатиричной системы счисления:
- Перевод чисел из шестнадцатеричной системы в десятичную требует больше вычислений, чем при использовании двоичной и восьмеричной систем;
- Использование шестнадцатеричной системы может быть сложным для людей, не знакомых с этой системой;
- При работе с большими числами в шестнадцатеричной системе может возникнуть сложность из-за ограниченного количества символов (цифры от 0 до 9 и буквы от A до F).
Несмотря на эти недостатки, восьмеричная и шестнадцатеричная системы счисления широко используются в компьютерных науках и программировании, так как они обладают определенными преимуществами, которые позволяют более эффективно работать с битами и байтами.
История восьмиричной и шестнадцатиричной систем счисления

Шестнадцатиричная система счисления, или гексадецимальная система, развилась из октальной системы. Она получила свое название потому, что каждый разряд числа может принимать значения от 0 до 15, что является шестнадцатеричной формой.
Хотя восьмичная и шестнадцатиричная системы счисления имеют свои корни в древности, они получили большую популярность в современной эпохе компьютеров. Это происходит потому, что эти системы счисления идеально подходят для работы с двоичными данными, которые широко используются в компьютерах.
Восьмеричная система счисления используется для представления групп трех двоичных разрядов. Каждому значению трех разрядов соответствует одна цифра восьмеричной системы счисления. Это позволяет сократить количество необходимых символов для представления двоичных данных и упростить манипуляции с ними.
Шестнадцатеричная система используется для представления группы четырех двоичных разрядов. Каждый набор четырех разрядов представляется одной цифрой шестнадцатеричной системы счисления. Это делает работу с двоичными данными еще более эффективной и удобной.
| Десятичная система | Восьмеричная система | Шестнадцатеричная система |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
| 7 | 7 | 7 |
| 8 | 10 | 8 |
| 9 | 11 | 9 |
| 10 | 12 | A |
| 11 | 13 | B |
| 12 | 14 | C |
| 13 | 15 | D |
| 14 | 16 | E |
| 15 | 17 | F |
Взаимодействие восьмиричной и шестнадцатиричной систем счисления с другими системами счисления
Восьмеричная и шестнадцатиричная системы счисления взаимодействуют с другими системами счисления в основном на уровне преобразования чисел из одной системы счисления в другую.
Если необходимо перевести число из восьмеричной системы счисления в десятичную, можно воспользоваться следующим способом:
- Умножить каждую цифру числа слева направо на степень восьмерки, начиная с 0 и увеличивая ее на единицу при движении вправо.
- Сложить полученные произведения.
Например, число 247 в восьмеричной системе можно перевести в десятичную следующим образом:
(2 × 8^2) + (4 × 8^1) + (7 × 8^0) = 2 × 64 + 4 × 8 + 7 × 1 = 128 + 32 + 7 = 167.
Аналогично, если требуется перевести число из шестнадцатиричной системы счисления в десятичную, можно воспользоваться следующим алгоритмом:
- Умножить каждую цифру числа слева направо на степень шестнадцати, начиная с 0 и увеличивая ее на единицу при движении вправо.
- Сложить полученные произведения.
Например, число 1A в шестнадцатиричной системе можно перевести в десятичную следующим образом:
(1 × 16^1) + (10 × 16^0) = 1 × 16 + 10 × 1 = 16 + 10 = 26.
Восьмеричная и шестнадцатиричная системы счисления также могут быть преобразованы в двоичную систему счисления. Для этого каждая цифра числа преобразуется в соответствующую двоичную последовательность.
Взаимодействие восьмеричной и шестнадцатиричной систем счисления с другими системами, такими как двоичная или десятичная, происходит посредством преобразования чисел из одной системы в другую. Это позволяет удобно выполнять различные математические операции и использовать разные базы для записи чисел в зависимости от задачи или требований.
Практическое применение восьмиричной и шестнадцатиричной систем счисления

Восьмиричная и шестнадцатиричная системы счисления часто применяются в различных областях, где нужно представлять числа, а также хранить и обрабатывать данные. Оба этих вида систем счисления имеют свои преимущества и особенности, которые делают их полезными в определенных ситуациях.
Восьмиричная система счисления основана на использовании восми чисел: 0, 1, 2, 3, 4, 5, 6, 7. Каждая цифра в восьмиричной системе представляет собой комбинацию трех двоичных цифр, что делает ее удобной для работы с битовыми данными. Например, восьмеричное число 12 представлено в двоичной системе как 1100. Восьмиричная система счисления часто используется в программировании, особенно при работе с компьютерными сетями и операционными системами.
Шестнадцатиричная система счисления использует шестнадцать символов: 0-9 и буквы A-F. Каждая цифра в шестнадцатиричной системе представляет собой комбинацию четырех двоичных цифр. Это делает ее особенно удобной для записи и передачи больших чисел и цветовых значений в графических программах. Например, число FF в шестнадцатиричной системе эквивалентно 255 в десятичной системе. Шестнадцатиричная система широко применяется в программировании, архитектуре компьютеров, базах данных и коммуникационных протоколах.
Восьмиричная и шестнадцатиричная системы счисления позволяют удобно представлять и работать с большими объемами данных, а также упрощают конвертацию чисел в различные системы. Понимание этих систем счисления позволяет разработчикам и специалистам в области компьютерных наук эффективно работать с данными и выполнять сложные вычисления.



