Вертикальный угол – это угол, который образуется двумя перпендикулярными прямыми. Он является одним из основных понятий геометрии и широко применяется в различных областях, включая строительство, архитектуру, физику и многие другие науки.
Вертикальные углы являются равными между собой. Это означает, что если два угла образуются пересекающимися прямыми, то они равны друг другу. Данное свойство вертикальных углов позволяет применять его при решении задач на нахождение неизвестных углов или нахождение значений других величин.
Вертикальные углы могут быть как прямыми (равны 90 градусам), так и острыми (меньше 90 градусов), а также тупыми (больше 90 градусов). Их сумма всегда равна 180 градусам. Это дает возможность использовать вертикальные углы для решения задач, связанных с определением неизвестных углов в треугольниках или многоугольниках.
Важно понимать, что вертикальные углы появляются только при пересечении двух прямых линий. Если мы имеем только одну прямую, то вертикальных углов не будет.
Знание свойств вертикальных углов является основой для понимания и решения задач по геометрии. Оно позволяет находить и использовать правильные углы при разработке и строительстве различных конструкций. Поэтому, осознавая все особенности вертикальных углов, можно более точно решать их применять в практике.
Что такое вертикальный угол и его свойства
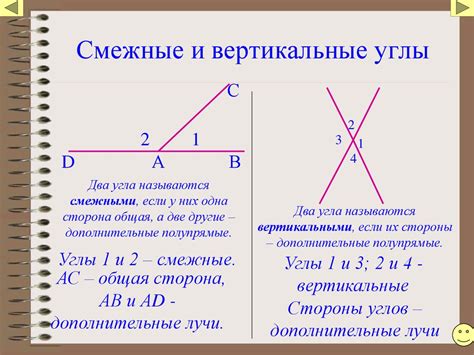
В математике вертикальным углом называется угол, соответствующий пересекающимся линиям или плоскостям и имеющий общую вершину. Вертикальный угол может быть образован двумя прямыми линиями (вертикальные линии) или двумя плоскостями (вертикальные плоскости), которые пересекаются под прямым углом.
Свойства вертикальных углов:
| Вертикальные углы равны друг другу: | если две прямые линии пересекаются, то образовавшиеся вертикальные углы будут равны между собой. |
| Сумма вертикальных углов равна 180 градусам: | если в вершине пересекающихся прямых линий имеется вертикальный угол, то суммой его и смежного угла будет образовываться прямой угол, который равен 180 градусам. |
| Вертикальные углы вместе образуют вертикальную пару: | когда две прямые линии пересекаются, все образовавшиеся вертикальные углы вместе образуют вертикальные пары. |
Изучение вертикальных углов является важным принципом в геометрии и нахождение равных углов в различных фигурах, что позволяет решать разнообразные задачи, связанные с построением и измерением углов.
Определение и значение вертикального угла

Основной особенностью вертикального угла является то, что его значение равно значению угла, ему противолежащего. То есть, если две прямые пересекаются и образуют вертикальный угол, то это значит, что углы, образующиеся с прямыми, равны по величине.
Значение вертикального угла может быть измерено в градусах, минутах и секундах. Обычно, для упрощения измерений, углы записываются в градусах.
Вертикальные углы играют важную роль в геометрии и представляют собой основу для понимания и изучения геометрических форм и отношений. Они также используются при решении задач, связанных с построением, преобразованиями или измерениями в геометрии.
Понимание и применение вертикального угла важно не только для математиков, но и для людей, работающих в строительстве, архитектуре, графическом дизайне и других областях, где требуется точное измерение и взаимное расположение объектов.
Угол, образующийся пересечением двух прямых
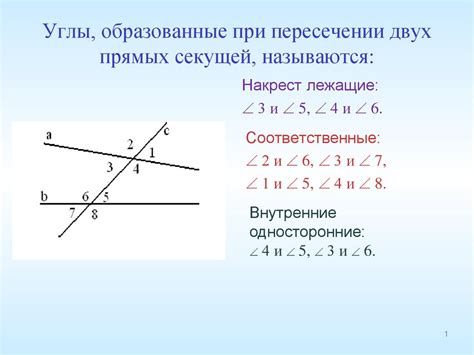
Основная особенность вертикальных углов заключается в их равенстве. Если две прямые пересекаются, то углы, расположенные по разные стороны от пересекающей прямой, будут вертикальными и они будут равны между собой. Это свойство позволяет упростить решение геометрических задач и использовать его для доказательства различных теорем.
Другой интересной особенностью вертикальных углов является их сумма. Если у нас есть два вертикальных угла, то их сумма будет всегда равна 180 градусам. Это вытекает из того факта, что две пересекающиеся прямые образуют пару вертикальных углов, которые составляют прямую. Таким образом, сумма всех вертикальных углов в данной системе будет равна 180 градусам.
Знание особенностей и свойств вертикальных углов позволяет решать разнообразные геометрические задачи, проводить доказательства и находить новые связи между углами и прямыми. Поэтому понимание этой концепции играет важную роль в изучении геометрии и математики в целом.
Особенности и свойства вертикального угла
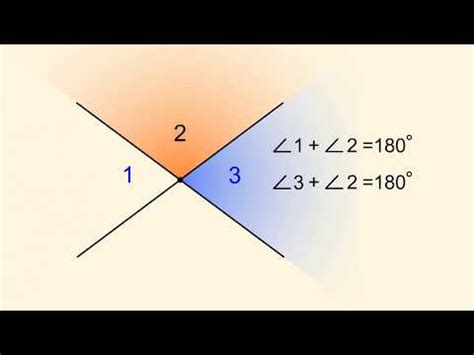
Таким образом, если в вертикальном угле один из углов равен, например, 30 градусов, то все остальные углы в этом угле также будут равны 30 градусов. Это является следствием свойства вертикальных углов: они всегда равны между собой.
Другим важным свойством вертикального угла является то, что сумма значений его внутренних углов всегда равна 180 градусов. Если один из углов вертикального угла равен, например, 60 градусов, то второй угол будет равен 120 градусов, чтобы общая сумма была 180 градусов.
Также стоит отметить, что вертикальные углы могут находиться не только на пересечении прямых линий, но и на пересечении прямых линий с плоскостями. Например, в случае пересечения прямой линии с горизонтальной плоскостью, образуется два вертикальных угла.
Вертикальные углы играют важную роль в геометрии и используются при решении различных геометрических задач. Зная свойства вертикального угла и умея с ними работать, можно упростить решение задач и получить более точные результаты.
Равенство вертикальных углов в геометрии
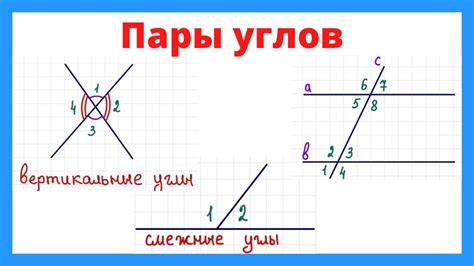
Вертикальные углы называются равными, если они имеют одинаковые меры. Если угол A равен углу B, то это означает, что их значение в градусах или радианах одинаково. Например, если угол A равен 60 градусам, то угол B также будет равен 60 градусам.
Равенство вертикальных углов является следствием свойств пересекающихся прямых линий. Когда две прямые линии пересекаются, они образуют четыре угла в точке пересечения. Два парных угла, которые лежат по разные стороны от пересечения и направлены в противоположные стороны, называются вертикальными углами.
Из свойств пересекающихся прямых линий следует, что вертикальные углы всегда равны между собой. Это означает, что если один вертикальный угол равен определенной мере, то другой вертикальный угол в точке пересечения будет иметь такую же меру.
Равенство вертикальных углов может быть использовано для решения геометрических задач. Например, если известна мера одного вертикального угла, то можно найти меру другого угла, используя свойство их равенства.
Вертикальные углы являются важными элементами геометрии и широко применяются при решении задач на плоскости. Понимание и использование свойства равенства вертикальных углов позволяет упростить решение геометрических задач и получить точные результаты.
Способы определения вертикальных углов
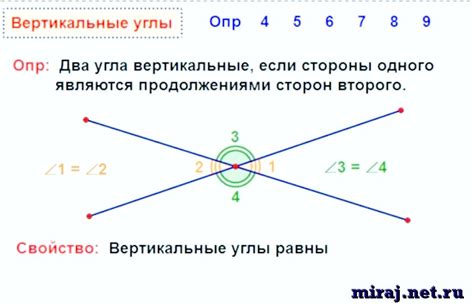
Существует несколько способов определения вертикальных углов:
Использование специального угломерного прибора:
Для определения угла можно использовать угломерный прибор, который обычно имеет форму полукруга. Необходимо разместить его таким образом, чтобы ось прибора совпадала с осью угла. Затем нужно ориентироваться по делениям на полукруге, чтобы определить величину угла.
Использование геодезических приборов:
Для определения вертикальных углов в геодезии используются специальные приборы, такие как нивелиры или теодолиты. Они позволяют точно измерить углы между горизонтальной и вертикальной плоскостями.
Использование геометрических принципов:
Вертикальные углы можно также определить с помощью геометрических принципов. Зная, что вертикальные углы равны друг другу, можно сравнить углы, используя другие известные углы или их величины.
Выбор метода определения вертикальных углов зависит от конкретной ситуации и доступных инструментов. В любом случае, правильное измерение и определение углов является важным элементом в различных областях, включая строительство, геодезию и геометрию.
Примеры и задачи с использованием вертикальных углов
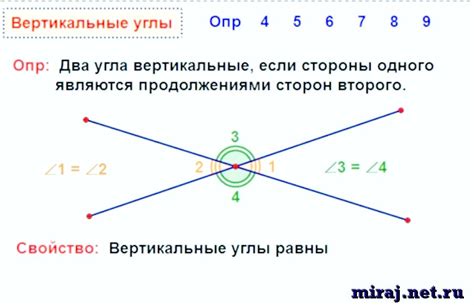
Вертикальные углы играют важную роль при решении различных задач и геометрических проблем. Ниже представлены некоторые примеры и задачи, в которых требуется использовать знания о вертикальных углах:
- Задача: На чертеже даны две прямые AB и CD, пересекающиеся в точке O. Найдите все пары вертикальных углов в этом чертеже.
- Задача: В треугольнике ABC, угол BAC равен 60 градусов. Найдите меру вертикального угла, образованного продолжением стороны AB и стороной AC.
- Пример: Если два угла образуют пару вертикальных углов, то каждый угол из этой пары будет иметь одинаковую меру.
- Пример: Если два угла суммарно равны 180 градусов, то они являются смежными вертикальными углами.
- Задача: В параллелограмме ABCD угол A равен 70 градусов. Найдите меру каждого из вертикальных углов, образованных продолжением стороны BC и стороной CD.
- Пример: В треугольнике ABC угол BAC и угол BCA образуют пару вертикальных углов. Найдите меру каждого из этих углов, если угол BAC равен 40 градусов.
Использование знания о вертикальных углах позволяет решать разнообразные задачи в геометрии и анализе различных фигур. Уверенное владение этим понятием позволяет более точно и эффективно решать геометрические задачи.
Равенство вертикальных углов в реальной жизни
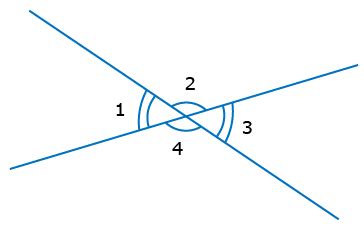
Понимание вертикальных углов и их особенностей играет важную роль не только в математике, но и в реальной жизни. Вертикальные углы встречаются повсюду и применяются в различных сферах деятельности.
Один из примеров, где вертикальные углы имеют большое значение, – это архитектура и строительство. При проектировании и возведении зданий, архитекторы и инженеры учитывают вертикальные углы для создания прочных и устойчивых конструкций. Равенство вертикальных углов позволяет достичь симметричности и гармонии в архитектуре.
Вертикальные углы также имеют важное значение в геодезии, где используются для определения высоты и углов наблюдений. Отсчет углов в геодезии позволяет точно измерять разницу высот между объектами и определять их координаты на поверхности Земли.
Еще одной сферой применения вертикальных углов является навигация и география. На картографических материалах и навигационных инструментах градусы и углы помогают определить направление движения и ориентацию в пространстве. Равенство вертикальных углов позволяет создавать точные и надежные карты, способствующие успешному перемещению по местности.
В медицине также применяются вертикальные углы. Например, в стоматологии при изготовлении и установке зубных протезов важно учесть вертикальные углы для обеспечения правильного прикуса и функционирования зубной системы.
Таким образом, вертикальные углы являются неотъемлемой частью нашей жизни. Понимание и использование этих углов в различных сферах помогает нам создавать прочные конструкции, точно измерять и определять направление, а также обеспечивать правильную функцию различных объектов и систем.
Применение вертикальных углов в инженерии и архитектуре

Одним из основных применений вертикальных углов является определение и контроль вертикальности строительных конструкций. Инженеры и архитекторы используют вертикальные углы для построения столбов, стен, башен и других вертикальных элементов зданий и сооружений. Правильно установленные вертикальные углы обеспечивают прочность и устойчивость конструкций, а также обеспечивают правильное функционирование систем отвода воды, электрических и тепловых сетей.
Вертикальные углы также используются при измерении высот и глубин различных объектов и ландшафтов. Инженеры применяют вертикальные углы для определения точного положения различных элементов инфраструктуры, например, при разработке дорожных сетей, туннелей и мостов. Архитекторы используют вертикальные углы для регулирования высоты потолков и окон, создания уровней и плоскостей в интерьерах зданий.
Другое важное применение вертикальных углов связано с измерением и контролем наклона и уклона поверхности. Инженеры и архитекторы используют вертикальные углы для определения и коррекции наклона дорог, площадок для парковки и зданий, что позволяет создавать безопасные и эффективные конструкции. Также вертикальные углы используются при создании систем дренажа, трубопроводов и канализации, чтобы обеспечить правильное движение жидкостей и газов.
В общем, вертикальные углы являются неотъемлемой частью работы инженеров и архитекторов. Они позволяют создавать прочные, устойчивые и функциональные конструкции, а также обеспечивают правильное положение элементов инфраструктуры и интерьеров. Без использования вертикальных углов оказалось бы очень сложным достичь точности и высокого качества в инженерных и архитектурных проектах.



