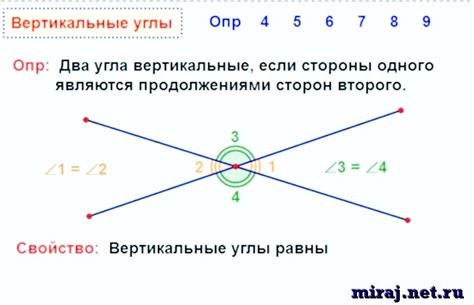
Вертикальные углы – одно из важнейших понятий в геометрии. Они являются одним из наиболее простых углов и характеризуются своей особой особенностью – они равны. Вертикальные углы образуются пересекающимися прямыми и отличаются от остальных углов тем, что их величина всегда одинакова.
Определить вертикальные углы очень просто. Для этого достаточно обратить внимание на пересекающиеся прямые. Если две прямые пересекаются, образуя при этом углы, и эти углы равны между собой, то они являются вертикальными. Иными словами, вертикальными углами будут две прямые, пересекающиеся под углом в 90 градусов.
Возникает вопрос: зачем нужно знать свойства и характеристики вертикальных углов? Ответ прост: такие углы являются основой для решения геометрических задач. Знание и понимание свойств вертикальных углов поможет ученикам не только успешно справляться с задачами на уроках геометрии, но и развить логическое мышление, улучшить навыки анализа и построения решений. Ведь вертикальные углы являются основой для понимания более сложных геометрических фигур и конструкций.
Что такое вертикальные углы
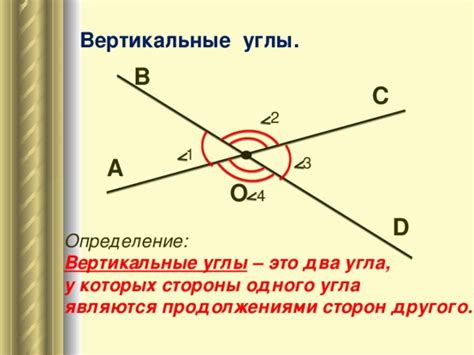
Основным свойством вертикальных углов является их равенство. Если две прямые пересекаются, то вертикальные углы, которые они образуют, равны между собой по величине.
Чтобы увидеть это свойство вертикальных углов, можно представить себе два перпендикулярно пересекающихся дерева.
| Вертикальные углы | Пример |
|---|---|
| Угол 1 | Угол 2 |
| Угол 3 | Угол 4 |
В данном примере угол 1 равен углу 2, а угол 3 равен углу 4, так как они являются вертикальными углами.
Из свойств вертикальных углов следует, что если один из вертикальных углов равен 90 градусам (прямому углу), то все остальные вертикальные углы тоже будут равны 90 градусам.
Изучение вертикальных углов является важным в геометрии и применяется в различных областях, таких как строительство, дизайн, архитектура и т.д.
Определение вертикальных углов
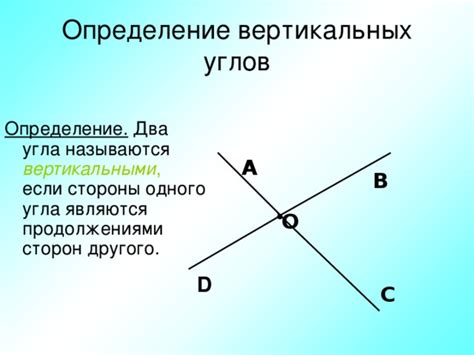
Вертикальными углами называют пару углов, которые расположены напротив друг друга и имеют общую вершину. Такие углы образуются при пересечении двух прямых линий. Вертикальные углы всегда равны между собой.
Если две прямые линии пересекаются в точке, то образовавшиеся вертикальные углы имеют одинаковые величины, то есть они равны своим соответствующим другим вертикальным углам.
Обозначается вертикальный угол символом ∠.
Знание свойств вертикальных углов является важным при решении задач на геометрию, а также в различных областях естественных и точных наук.
Геометрические свойства вертикальных углов
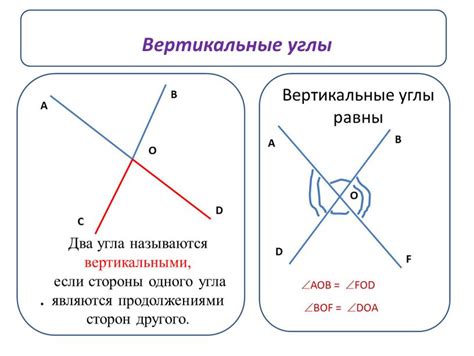
Если две прямые пересекаются, то вертикальные углы, образованные этими прямыми, будут всегда равны друг другу. Это свойство можно использовать при доказательствах и решении геометрических задач.
Другое свойство вертикальных углов – их дополнительность. Если две прямые пересекаются, то вертикальные углы дополняют друг друга до полного угла (180 градусов).
Вертикальные углы могут быть полезны при нахождении значений других углов, а также при решении задач на построение и расстояния.
| Свойство | Формулировка |
| Равенство | Вертикальные углы, образованные пересекающимися прямыми, равны друг другу. |
| Дополнительность | Вертикальные углы, образованные пересекающимися прямыми, дополняют друг друга до полного угла (180 градусов). |
Изучение свойств вертикальных углов является важной частью геометрии и может быть полезным при решении различных геометрических задач, конструкциях и доказательствах.
Взаимное расположение вертикальных углов
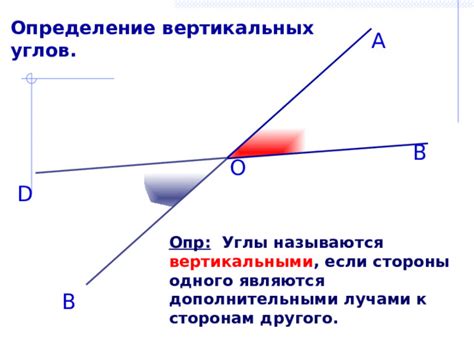
Одно из основных свойств вертикальных углов – величины этих углов равны между собой. Другими словами, если у нас имеется два угла, вершины которых расположены вертикально друг над другом, то они будут равными по величине. Такое свойство вертикальных углов позволяет легко находить нужные углы и решать геометрические задачи.
Кроме того, вертикальные углы также обладают свойством суммы. Если мы имеем два вертикальных угла, то их сумма будет равна 180 градусам. Это свойство следует из того факта, что углы, дополняющие друг друга и образующие прямую, всегда равны 180 градусам.
| Взаимное расположение вертикальных углов | Свойство |
|---|---|
| Величины углов | Равны |
| Сумма углов | Равна 180 градусам |
Формула для вычисления вертикальных углов

Для вычисления вертикальных углов используется следующая формула:
| Угол 1 | Угол 2 |
|---|---|
| Угол 3 | Угол 4 |
Формула гласит: угол 1 равен углу 3, а угол 2 равен углу 4. То есть, если у нас есть две пары вертикальных углов, мы можем утверждать, что они равны друг другу.
Вычисление вертикальных углов может быть полезным при решении задач по геометрии, особенно при работе с параллельными прямыми и пересекающимися прямыми.
Практическое применение вертикальных углов

Одно из практических применений вертикальных углов - это решение задач на построение фигур. Например, в задачах на построение параллелограмма или прямоугольника на плоскости, знание свойств вертикальных углов позволяет определить необходимые углы и длины сторон фигуры.
Вертикальные углы также используются при решении задач на вычисление неизвестных углов. Например, в задачах на расчет углов в треугольниках или многоугольниках, зная значение одного из вертикальных углов, можно найти значения остальных.
Вертикальные углы также находят применение в решении задач на распределение и перемещение объектов. Например, при размещении мебели в комнате или на планировке помещения, знание свойств вертикальных углов помогает расположить предметы таким образом, чтобы они выглядели гармонично.
Таким образом, понимание и применение свойств вертикальных углов является важным инструментом при решении практических задач в геометрии и других областях, где требуется работа с углами и фигурами.
Симметричные относительно вертикальных углы

Если две прямые пересекаются, то образовавшиеся четыре угла делятся на пары, которые называются симметричными относительно вертикальных углов. Симметричные углы равны между собой.
Например, если две параллельные прямые пересекаются нижними поперечными, то образовавшиеся вертикальные углы являются симметричными. Зная один из вертикальных углов, мы можем найти значению другого вертикального угла.
Из этих свойств вертикальных углов следует, что если две прямые пересекаются, то вертикальные углы симметричны относительно своей общей биссектрисы.
Значение вертикальных углов в архитектуре
Углы, образующиеся на пересечении двух вертикальных стен, определяют форму и структуру здания, его визуальные пропорции и гармонию.
Архитекторы и дизайнеры могут использовать разные формы и величины вертикальных углов, чтобы создать разнообразные эффекты и выразить идею здания.
Острые вертикальные углы могут придать зданию ощущение стремительности и динамичности, а наоборот, широкие углы создают ощущение устойчивости и спокойствия.
Кроме того, вертикальные углы могут иметь символическое значение, отражая идеалы и ценности, связанные с зданием. Например, острые и резкие углы могут символизировать современность и динамизм, в то время как закругленные и гладкие углы могут ассоциироваться с гармонией и уютом.
Если вертикальные углы здания согласуются с горизонтальными линиями и другими элементами архитектуры, это может создать визуально привлекательный образ и придать зданию особую грацию и элегантность.
Таким образом, вертикальные углы в архитектуре не только служат функциональной роли, определяя конструкцию здания, но и играют важную роль в создании его образа и атмосферы.
Важность понимания вертикальных углов

Одним из основных свойств вертикальных углов является то, что они равны по величине. Это означает, что при пересечении двух прямых линий, образующиеся вертикальные углы будут одинаковыми. Это свойство позволяет упрощать решение задач и проведение доказательств.
Вертикальные углы также используются при измерении и описании поворотов и поворотных устройств. Например, при проектировании и построении роторного механизма или регулирующего устройства, необходимость понимания вертикальных углов не может быть переоценена. Точное позиционирование и выравнивание элементов в процессе сборки и эксплуатации обеспечивает его долговечность и эффективность работы.
В геодезии и картографии понимание вертикальных углов также играет важную роль. Определение высоты объектов относительно уровня моря или географической системы требует знания вертикальных углов и их применения при измерении углов наклона и удаленности точек.
Таким образом, понимание вертикальных углов является неотъемлемой частью геометрии и находит применение в различных областях. Правильное использование свойств и знание методов измерения и решения задач с использованием вертикальных углов позволяет достичь более точных и эффективных результатов в различных профессиональных сферах.



