В геометрии есть много интересных и удивительных фактов о треугольниках, одна из которых касается равносторонних треугольников. Мы все слышали, что все стороны равностороннего треугольника имеют одинаковую длину. Но может ли быть что-то еще общее у этих треугольников?
Оказывается, равносторонние треугольники имеют не только одинаковые стороны, но и одинаковые углы. Это означает, что каждый угол равностороннего треугольника равен 60 градусам. Таким образом, все равносторонние треугольники подобны друг другу.
Подобность равносторонних треугольников в геометрии
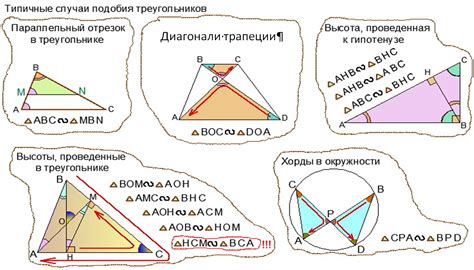
Равносторонний треугольник – это треугольник, у которого все три стороны равны. Важно отметить, что равносторонние треугольники являются особым случаем равнобедренных треугольников, у которых также две стороны равны.
Для того чтобы определить, являются ли два равносторонних треугольника подобными, нужно проверить выполнение двух условий:
1. Углы треугольников должны быть равными. В равностороннем треугольнике все три угла равны 60 градусам, поэтому если у двух треугольников соответствующие углы равны, то они являются подобными.
2. Соотношение длин сторон должно быть одинаковым. Поскольку у равностороннего треугольника все стороны равны, для подобных треугольников соотношение длин сторон также должно быть одинаковым. Например, если первый треугольник имеет стороны длиной 3, то второй треугольник должен иметь стороны длиной 6, так как это соотношение равно половине соответствующих длин.
Таким образом, все равносторонние треугольники являются подобными, но не все подобные треугольники являются равносторонними. Подобность треугольников является важным понятием при решении задач геометрии и позволяет упростить расчеты и доказательства.
Следует помнить, что подобность треугольников справедлива для любых размеров и может применяться в различных сферах, таких как архитектура, инженерия, физика и другие. Подобные треугольники имеют одинаковую форму, но различные размеры.
Основные понятия и определения

Для того чтобы понять, почему все равносторонние треугольники подобны, необходимо уяснить несколько важных понятий из геометрии.
- Треугольник - это фигура, состоящая из трех линейных сегментов, называемых сторонами, и трех точек пересечения этих сторон, называемых вершинами.
- Равносторонний треугольник - это треугольник, у которого все стороны равны друг другу. Все углы равностороннего треугольника также равны и составляют 60 градусов.
- Подобие треугольников - это свойство треугольников, при котором соответственные углы треугольников равны между собой, а соответственные стороны пропорциональны.
Итак, равносторонний треугольник - это треугольник, у которого все стороны равны, а подобие треугольников - это свойство, при котором углы равны и стороны пропорциональны. Далее мы рассмотрим, почему все равносторонние треугольники подобны и почему это свойство выполняется только для равносторонних треугольников.
Условия подобности равносторонних треугольников
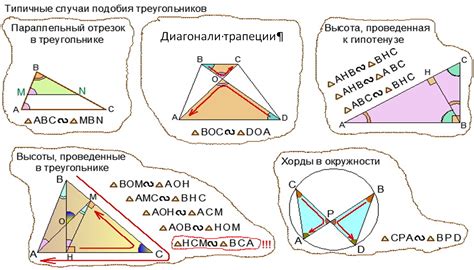
Для того чтобы два равносторонних треугольника можно было назвать подобными, нужно, чтобы выполнялись определенные условия.
Первое условие – равные стороны. Пусть у нас есть два треугольника ABC и DEF, и все их стороны равны: AB = BC = AC и DE = EF = DF. В этом случае треугольники подобны.
Второе условие – равные углы. Если углы при основаниях треугольников ABC и DEF будут равными: ∠BAC = ∠EDF и ∠BCA = ∠EFD, то треугольники ABC и DEF также будут подобными.
Подводя итог, можно сказать, что два равносторонних треугольника будут подобными, если все их стороны равны и у них равны все углы при основаниях.
Применение подобия равносторонних треугольников в практических задачах
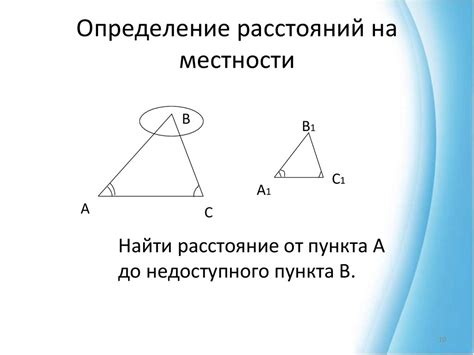
1. Расчет высоты пирамиды или конуса. Если известна длина ребра равностороннего треугольника, можно использовать его подобные треугольники для определения высоты пирамиды или конуса. Путем проведения прямых, перпендикулярных основанию и проходящих через вершину, можно найти высоту.
2. Построение фигур. Подобные равносторонние треугольники могут использоваться для построения сложных фигур. Путем масштабирования или увеличения размеров равносторонних треугольников можно создать разнообразные формы.
3. Рассчет площадей. Используя подобные равносторонние треугольники, можно рассчитать площадь не только самого треугольника, но и других фигур. Например, если треугольник является основанием пирамиды, можно рассчитать площадь ее боковой поверхности.
4. Построение треугольников с определенными углами. Зная углы равностороннего треугольника, можно построить другие треугольники с определенными углами, используя подобие. Это может быть полезно при дизайне и строительстве.



