Группы – это одна из основных понятий в различных областях знаний, от социологии и психологии до математики и физики. Они представляют собой совокупности людей или объектов, которые объединены определенным образом. В группах происходят взаимодействия, формируются отношения и развиваются динамика, что делает их предметом изучения и интереса исследователей.
Основное понятие группы – это совокупность лиц или элементов, которые обладают общими характеристиками или целями. Группы могут быть разделены на подгруппы или классы, и находиться внутри более крупных групп. Возможны различные критерии для определения групп, например, группа по интересам, по возрасту или по рабочим командам. Однако, независимо от принадлежности к конкретной группе, взаимодействие и коммуникация – ключевые факторы для ее формирования и функционирования.
Группы играют важную роль в обществе и оказывают воздействие на поведение и самоощущение ее членов. Они предоставляют людям возможность общаться, делиться информацией и ресурсами, а также ощущать свою причастность и идентичность. Внутри группы проявляются разные роли и статусы, возникают социальные нормы и ожидания, которые формируют поведение и взаимодействие ее участников.
Что такое группы

Группы могут быть различных типов и формироваться по разным принципам. Они могут быть статическими и динамическими. Статическая группа представляет собой фиксированный набор элементов, который не изменяется со временем. Динамическая группа может изменять свой состав, добавлять или удалять элементы в зависимости от определенных условий или критериев.
Группы могут использоваться в различных областях, таких как информационные технологии, социология, психология, управление и др. Например, в информационных системах группы используются для организации и классификации данных, а в социологии – для изучения социальных групп и их взаимодействия.
Основное понятие группы – это объединение элементов по общим характеристикам или свойствам. Оно помогает систематизировать информацию, облегчает работу с данными и позволяет получать более полное представление об объектах или явлениях, находящихся в составе группы.
Различные интерпретации понятия

Понятие "группа" имеет различные интерпретации в разных областях знания. Рассмотрим несколько основных толкований этого понятия:
- Математика: в математике группа - это алгебраическая структура, состоящая из множества элементов и операции, удовлетворяющих определенным аксиомам. Группы широко применяются в различных областях математики и физики, например, в теории чисел и теории групп.
- Социология: в социологии группа - это совокупность людей, объединенных общими интересами, целями или идеалами. Группы могут быть формальными (например, организации) и неформальными (например, друзья, семья).
- Психология: в психологии группа - это совокупность индивидуумов, взаимодействующих друг с другом и влияющих на поведение и мировоззрение каждого участника. Группы могут быть малыми (например, семья) или большими (например, сообщество).
- Биология: в биологии группа - это совокупность организмов, которые связаны между собой определенными взаимоотношениями. Группы в биологии могут быть различных типов, например, стаи животных или колонии бактерий.
Таким образом, понятие "группа" имеет много различных интерпретаций в зависимости от контекста, в котором оно используется. Понимание этих различий позволяет лучше понять сущность и роль группы в различных областях человеческой деятельности.
Математическое определение группы
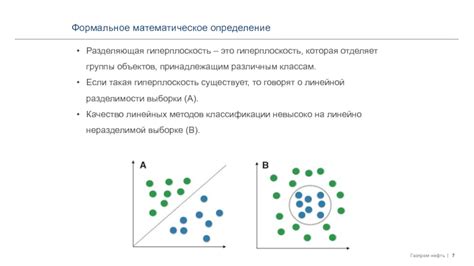
Элементы группы обозначаются обычно символами a, b, c и так далее. Группа может быть конечной, то есть состоять из конечного числа элементов, или бесконечной, то есть иметь бесконечное число элементов. Операция, определенная на множестве элементов группы, обозначается обычно символом "*", "∘" или "+", и называется групповой операцией.
Для того чтобы группа удовлетворяла определенным аксиомам, она должна обладать следующими свойствами:
- Закон замыкания: для любых элементов a и b из группы, результат операции также должен принадлежать к группе.
- Ассоциативность: для любых элементов a, b и c из группы, результат операции (a * b) * c должен быть равен a * (b * c).
- Существование нейтрального элемента: в группе должен существовать элемент e, для которого выполнено a * e = e * a = a для любого элемента a.
- Существование обратного элемента: для любого элемента a из группы должен существовать элемент b, такой что a * b = b * a = e, где e - нейтральный элемент.
Эти свойства группы позволяют выполнять операции с элементами группы, обеспечивая ее алгебраическую связность и структурированность. Математические группы являются фундаментальным объектом изучения в алгебре и находят применение в различных областях, включая физику, криптографию и компьютерные науки.
Ключевые характеристики группы

Вот некоторые из ключевых характеристик группы:
| 1. Взаимодействие и коммуникация | Группа предполагает взаимодействие между ее членами. Коммуникация может быть осуществлена различными способами - устно, письменно или виртуально. Важное значение имеет возможность общения и обмена информацией. |
| 2. Совместная цель | Группа объединяется вокруг общей цели или задачи. Она имеет коллективные интересы и решает общие проблемы или задачи. Цель может быть достигнута только совместными усилиями членов группы. |
| 3. Взаимозависимость | Члены группы взаимозависимы друг от друга. Каждый вносит свой вклад в достижение общей цели и получает выгоду от сотрудничества с другими участниками. Взаимозависимость создает чувство сопричастности и взаимного поддержки. |
| 4. Определенная структура | Группа имеет определенную структуру с ролями и ответственностями для каждого ее члена. Важно определить лидера группы, регулировать коммуникацию и обеспечивать согласованность в работе группы. |
| 5. Взаимное влияние | Члены группы оказывают влияние друг на друга. Отношения внутри группы, поддержка и социальная динамика могут повлиять на мнения, взгляды и поведение каждого члена группы. |
| 6. Социальная идентификация | Принадлежность к группе влияет на самоопределение членов и формирует их социальную идентичность. Группа удовлетворяет психологическим и социальным потребностям людей. |
Понимание ключевых характеристик группы помогает лучше понять ее сущность и функционирование. Эти характеристики формируют основной каркас группы и определяют ее цели, взаимодействие и успех в достижении общей задачи.
Примеры практических применений
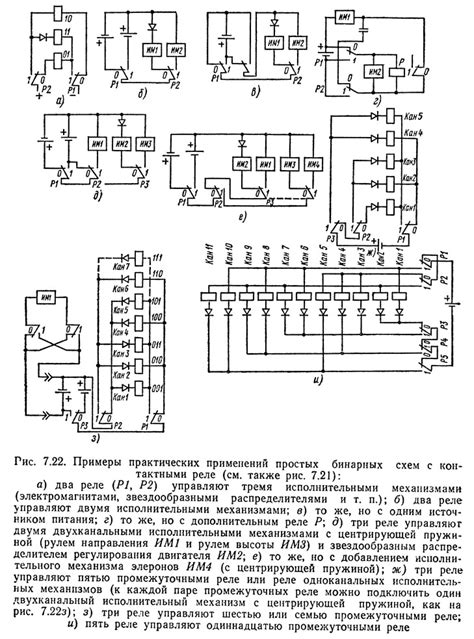
Группы имеют широкий спектр практических применений в различных областях.
В социальных науках группы используются для исследования социальных взаимодействий и формирования сообществ. Социологи и психологи изучают группы, чтобы понять, как люди взаимодействуют друг с другом и как формируются социальные структуры. Группы также применяются в организационном менеджменте для анализа динамики рабочих групп и оптимизации командной работы.
В информационных технологиях группы часто используются для организации и структурирования данных. Например, в базах данных группы могут использоваться для группировки и классификации информации. Веб-разработчики могут создавать группы, чтобы организовать элементы на веб-странице и упростить их стилизацию с помощью CSS.
В логистике и снабжении группы применяются для координации поставок и управления запасами. Группы товаров могут быть созданы на основе их характеристик, таких как тип, производитель, цена и др. Это упрощает работу с поставщиками и позволяет эффективно планировать складские запасы.
В искусстве и дизайне группы используются для создания композиции и упорядочивания элементов. Художники и дизайнеры могут группировать объекты на холсте или в макете, чтобы создать баланс и визуальный порядок.
| Область | Примеры применений |
|---|---|
| Социальные науки | Исследование социальных взаимодействий, анализ командной работы |
| Информационные технологии | Организация данных, упрощение стилизации веб-страниц |
| Логистика и снабжение | Координация поставок, управление запасами |
| Искусство и дизайн | Создание композиции, упорядочивание элементов |



