Четырехугольник – это совершенно удивительная фигура, которая может иметь самые разнообразные свойства и особенности. Одним из наиболее интересных классов четырехугольников являются выпуклые четырехугольники. Они выделяются своей особой структурой и обладают рядом уникальных свойств.
Выпуклый четырехугольник abcd – это фигура, все углы которой являются не только меньше 180 градусов, но и лежат все на одной полуокружности. Именно поэтому такой четырехугольник называется выпуклым. Несмотря на свою простоту, он обладает множеством интересных особенностей, которые активно изучаются в геометрии.
Важно отметить, что в выпуклых четырехугольниках также выполняются некоторые важные свойства. Например, сумма внутренних углов этой фигуры всегда будет равна 360 градусам. Кроме того, отрезки ab, bc, cd и da никогда не пересекаются. Такие особенности делают выпуклый четырехугольник abcd весьма уникальным и интересным объектом геометрии.
Свойства и особенности выпуклого четырехугольника abcd

Одно из свойств выпуклого четырехугольника abcd - это то, что его противоположные стороны параллельны. Это означает, что стороны ab и cd, а также стороны bc и da, являются параллельными и не пересекаются.
Все углы внутри выпуклого четырехугольника abcd являются острыми, то есть меньше 90 градусов. Это свойство позволяет нам классифицировать выпуклые четырехугольники по количеству прямых углов.
Еще одна особенность выпуклого четырехугольника abcd - это то, что сумма всех его углов равна 360 градусов. Это можно легко проверить, сложив все углы внутри фигуры: <abc + <bcd + <cda + <dab = 360 градусов.
Выпуклый четырехугольник также имеет диагонали - линии, соединяющие его несоседние вершины. В четырехугольнике abcd есть две диагонали: ac и bd. Диагонали делят фигуру на четыре треугольника: abc, bcd, cda и dab.
Также внутри выпуклого четырехугольника abcd есть много параллелограммов. Например, стороны ab и cd параллельны и равны друг другу, а также стороны bc и da. Это означает, что abcd можно рассматривать как четырехугольник с равными сторонами и параллельными сторонами.
Геометрические свойства направлений сторон
В выпуклом четырехугольнике abcd каждая из его сторон имеет определенное направление, которое описывается относительно других сторон. Геометрические свойства направлений сторон помогают понять особенности формы и структуры четырехугольника.
Рассмотрим следующие случаи:
| Случай | Описание |
|---|---|
| 1 | Все стороны направлены снаружи четырехугольника |
| 2 | Одна сторона направлена внутрь четырехугольника |
| 3 | Две стороны направлены внутрь четырехугольника |
| 4 | Три стороны направлены внутрь четырехугольника |
Каждый из этих случаев имеет свои уникальные свойства и особенности. Например, в случае 1 все стороны выпуклого четырехугольника направлены снаружи, что означает, что углы внутри четырехугольника будут острыми. В случае 2, когда одна сторона направлена внутрь, будут существовать тупые углы внутри четырехугольника.
Таким образом, геометрические свойства направлений сторон являются важными при изучении выпуклых четырехугольников и позволяют более глубоко понять их структуру и форму.
Выпуклая комбинация внутренних и внешних углов
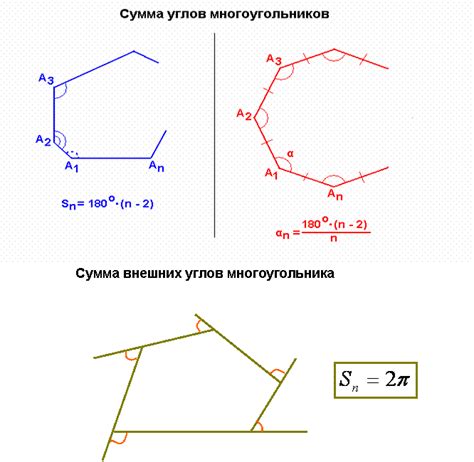
Выпуклый четырехугольник abcd имеет интересные свойства и особенности, связанные с комбинацией внутренних и внешних углов. В данном контексте, внутренние углы образуются между сторонами четырехугольника, в то время как внешние углы образуются продолжением сторон за пределами фигуры.
Когда речь идет о выпуклой комбинации внутренних и внешних углов, она может включать различные комбинации измерений углов и их сумм. Например, сумма двух внутренних углов может равняться сумме двух внутренних углов, а сумма двух внешних углов может быть равной сумме двух внешних углов.
Эти соотношения между углами выпуклого четырехугольника abcd могут иметь значимое значение при решении геометрических задач и нахождении неизвестных углов и сторон.
| Угол a | Угол b | Угол c | Угол d | |
|---|---|---|---|---|
| Внутренние углы | <a | <b | <c | <d |
| Внешние углы | >180 - a | >180 - b | >180 - c | >180 - d |
| Выпуклая комбинация | <a + >180 - d | <b + >180 - c | <c + >180 - b | <d + >180 - a |
Таблица выше показывает соотношение между внутренними углами, внешними углами и выпуклой комбинацией углов в четырехугольнике abcd. Знание этих соотношений может помочь в понимании геометрических свойств и особенностей фигуры.
Выпуклый четырехугольник abcd является фигурой с уникальными и интересными свойствами, которые можно исследовать и применять для решения различных математических задач.



