Треугольник mnk является одним из классических объектов в геометрии. В данной статье мы рассмотрим треугольник mnk, в котором значение стороны n равно 50. Это позволяет нам изучить его основные характеристики и свойства, а также обратить внимание на некоторые интересные аспекты этого треугольника.
Характеристики треугольника mnk: в данном случае, треугольник mnk является неправильным треугольником, так как его стороны не равны между собой. Одна из сторон (сторона n) равна 50, а остальные стороны (стороны m и k) могут иметь произвольное значение. Таким образом, треугольник mnk - это треугольник с одной стороной фиксированной длины и двумя изменяемыми сторонами.
Свойства треугольника mnk: треугольник mnk обладает всеми основными свойствами треугольника. Он имеет три угла, сумма которых равна 180 градусов. Также треугольник mnk может быть классифицирован по длинам его сторон: равносторонний (если m=k), равнобедренный (если m=k, но n отличается) или разносторонний (если m≠k).
Характеристики треугольника mnk: n=50
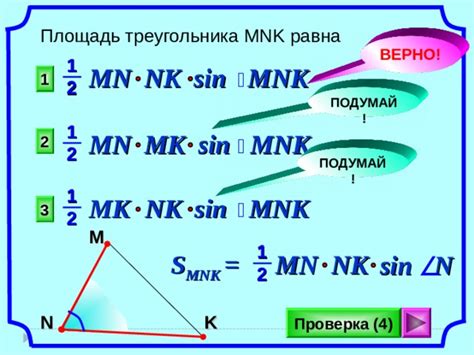
- Треугольник mnk является прямоугольным, если и только если сумма квадратов сторон m и n равна квадрату стороны k.
- Угол между сторонами m и n в треугольнике mnk может быть найден с помощью формулы тангенса угла между этими сторонами: tg(alpha) = m/n.
- Периметр треугольника mnk можно найти как сумму всех его сторон: P = m + n + k.
- Площадь треугольника mnk можно найти с помощью формулы Герона: S = sqrt(p * (p - m) * (p - n) * (p - k)), где p - полупериметр.
- В треугольнике mnk сумма всех углов равна 180 градусов, так как это свойство является общим для всех треугольников.
Зная эти характеристики и свойства треугольника mnk, можно более подробно изучать его свойства, проводить геометрические и алгебраические вычисления, а также использовать его в различных математических задачах и моделях.
Формула и основные свойства треугольника mnk: n=50
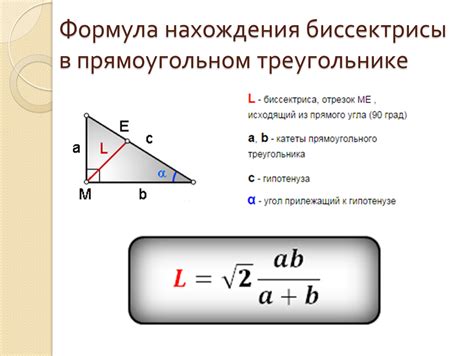
- Треугольник mnk имеет три стороны: mn, mk и nk.
- Сумма всех углов треугольника mnk равна 180 градусам.
- Треугольник mnk может быть разделен на два прямоугольных треугольника, имеющих общую сторону и прямой угол.
- Сторона mn противолежит углу с мерой 50 градусов.
- Треугольник mnk может быть рассмотрен как состоящий из двух прямоугольных треугольников mnq и nqk, где nq - высота треугольника mnk, опущенная из вершины n.
С использованием формул геометрии, можно вычислить длину сторон и площадь треугольника mnk. Для этого необходимо знать длины двух сторон и угол между ними.
Из свойства треугольника mnk с углом 50 градусов следует, что угол nmk также равен 50 градусам. Это делает треугольник mnk равнобедренным, так как две стороны mn и mk равны друг другу.
Основная формула, позволяющая вычислить площадь треугольника mnk, называется формулой полупериметра. Она выглядит следующим образом:
S = √(s * (s - mn) * (s - mk) * (s - nk)),
где S - площадь треугольника, mn, mk и nk - стороны треугольника, а s - полупериметр треугольника, вычисляемый как s = (mn + mk + nk) / 2.
Таким образом, зная длины сторон треугольник mnk и используя указанную формулу, можно вычислить его площадь.



