Треугольник – это геометрическая фигура, которая определяется тремя сторонами. В зависимости от значений этих сторон, треугольники могут быть различными: равносторонними, равнобедренными или разносторонними.
В данной статье речь пойдет о треугольнике def, в котором известна одна из его сторон – d = 52. Это значение позволяет нам рассмотреть некоторые особенности данного треугольника и вычислить значения других его сторон и углов.
Заметим, что буквы d, e, f обычно используют для обозначения сторон треугольника. Таким образом, сторону d можно отнести к одной из сторон треугольника def.
Описание треугольника def
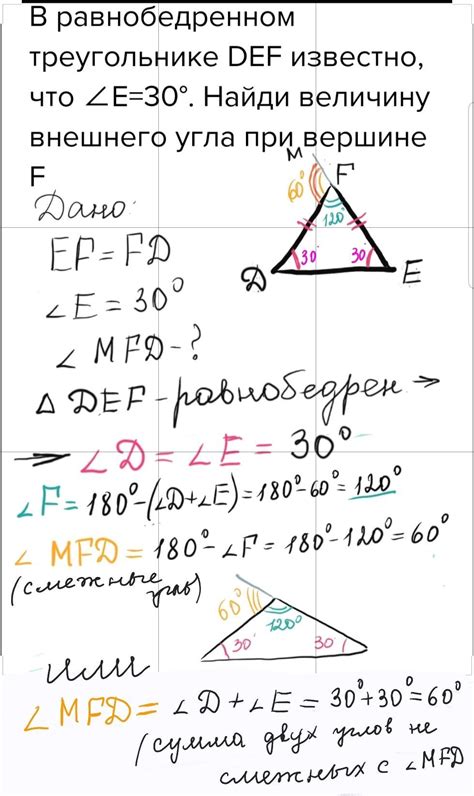
Также известно, что треугольник def может быть различных типов в зависимости от значений остальных сторон и углов. Вид треугольника определяется с помощью соотношения между сторонами и углами:
Стороны треугольника:
Сторона e - [описать сторону e].
Сторона f - [описать сторону f].
Углы треугольника:
Угол E - [описать угол E].
Угол F - [описать угол F].
Для полного описания треугольника def необходимо знать значения остальных сторон и углов.
Также важно отметить, что сумма углов треугольника всегда равна 180 градусам.
Известное значение стороны d

В треугольнике def известно, что сторона d равна 52.
Значение стороны d является известной величиной и определено как 52. Из данного треугольника нельзя однозначно определить другие стороны или углы, поскольку для полной информации о треугольнике необходимо знать еще две измеряемые стороны или углы.
Однако, имея значение стороны d, можно вывести различные математические соотношения, связанные с треугольником def.
В дальнейшем, зная другие измеряемые стороны или углы треугольника def, можно применять различные формулы и теоремы, чтобы получить дополнительную информацию о треугольнике, такую как длины других сторон, значения углов, площадь и периметр.
Значение сторон e и f
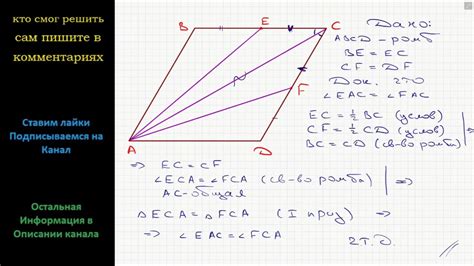
В треугольнике def, где одна из сторон известна, а именно d = 52, можно вычислить значения других сторон. По определению треугольника, сумма всех трех его сторон равна некоторому постоянному значению. Таким образом, для нахождения значений сторон e и f, необходимо знать значение третьей стороны.
Однако, можно сделать некоторые предположения о возможных значениях сторон e и f. Если треугольник def является прямоугольным, то по теореме Пифагора можно найти длину сторон e и f. Другими словами, если угол при вершине d составляет 90 градусов, то:
e2 + f2 = d2
Однако, без дополнительных данных, нельзя точно определить значения сторон e и f в треугольнике def. Для этого требуется знание длин других сторон или углов треугольника.
Используя информацию о значении стороны d = 52, можно исследовать геометрические свойства треугольника def и вывести дальнейшие уравнения для нахождения значений сторон e и f. Однако, для этого требуются дополнительные данные о треугольнике.
Знание значений сторон e и f позволит полностью определить геометрическую форму треугольника def и использовать его в различных вычислениях и анализах.
Нахождение углов
В треугольнике def, где один из углов обозначен как d и равен 52 градусам, можно найти остальные углы.
Для этого можно воспользоваться следующими свойствами треугольника:
- Сумма всех углов треугольника равна 180 градусам.
- В треугольнике можно использовать свойство синуса для нахождения угла по соотношению между сторонами и противолежащими углами.
Используя эти свойства, можно найти остальные углы треугольника def:
- Известно, что сумма всех углов треугольника равна 180 градусам. Поэтому можно вычислить угол e, используя формулу: e = 180 - d - f.
- После нахождения угла e, остается найти угол f, используя свойство синуса: sin(f) = (sin(d) / sin(e)) * h, где h - противолежащая сторона треугольника.
Таким образом, зная значение угла d и используя свойства треугольника, можно вычислить значения остальных углов треугольника def.
Вычисление площади
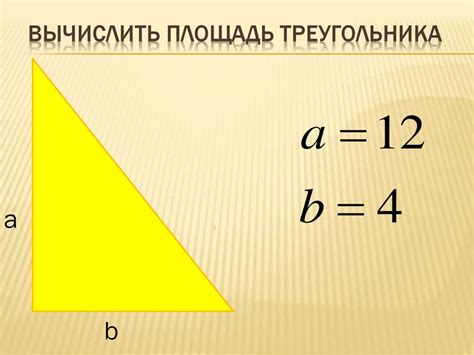
Площадь треугольника можно вычислить, зная его стороны и высоту или зная длины двух сторон и угол между ними. В данном случае, известно, что длина стороны d треугольника def равна 52. Для вычисления площади различными способами, можно воспользоваться следующими формулами:
- По длинам сторон и высоте:
- По длинам двух сторон и углу между ними:
Площадь треугольника равна половине произведения длины стороны на высоту, проведенную к этой стороне. Для этого необходимо найти высоту h и затем применить формулу:
S = (d * h) / 2
Площадь треугольника равна половине произведения длин сторон a и b на синус угла α между ними. Для этого необходимо найти угол α и затем применить формулу:
S = (a * b * sin(α)) / 2
Выберите подходящую для вас формулу и подставьте известные значения, чтобы вычислить площадь треугольника def.
Проверка на существование

В геометрии треугольник считается существующим, если сумма двух его сторон больше третьей стороны. Давайте проверим, выполнены ли условия существования треугольника def.
У нас дано, что сторона d треугольника def равна 52.
Если мы хотим узнать, существует ли такой треугольник, нам нужно знать значения остальных двух сторон e и f.
Давайте предположим, что e = 34 и f = 18.
Теперь проведем проверку:
Сумма сторон d и e равна 52 + 34 = 86.
Сумма сторон e и f равна 34 + 18 = 52.
Сумма сторон d и f равна 52 + 18 = 70.
Мы видим, что сумма сторон d и e больше стороны f, сумма сторон e и f больше стороны d, и сумма сторон d и f больше стороны e.
Таким образом, условия существования треугольника def выполняются, и треугольник с такими сторонами существует.
Однако, стоит отметить, что существуют и другие комбинации значений сторон e и f, которые могут также удовлетворять условиям существования треугольника def.
Значит, для проверки существования треугольника def необходимо знать значения остальных двух сторон e и f.
Важно не забывать проводить проверку на существование треугольника перед использованием его в дальнейших расчетах и задачах!
Применение в практике

В треугольнике def, где одна из сторон равна d=52, можно использовать известные длины сторон для решения различных задач в практике.
Например, зная длину стороны d и два угла треугольника, можно вычислить значения остальных сторон и углов с помощью геометрических формул и теорем. Это может быть полезно при построении домов, мостов, архитектурных объектов и других конструкций.
Также, в практике можно использовать известные длины сторон для нахождения площади треугольника. Для этого можно применить формулу Герона, которая позволяет вычислить площадь треугольника по длинам его сторон.
Другим примером применения известной длины стороны d=52 может быть вычисление высоты треугольника. При известной длине стороны и соответствующего ей угла можно использовать формулы тригонометрии для нахождения высоты треугольника.
Таким образом, зная длину стороны d=52 в треугольнике def, можно применить ее для решения различных задач в практике, связанных с вычислением длин сторон, углов, площади и высоты треугольника.



