Треугольник - это геометрическая фигура, состоящая из трех сторон и трех углов. Он является одной из основных фигур в геометрии и имеет много интересных свойств и формул.
В данной статье мы рассмотрим треугольник abc, в котором одна из сторон - ac, равна 52. Давайте вспомним, что такое прямая линия и как она связана со сторонами треугольника.
Прямая линия - это линия, у которой все точки расположены на одной прямой. В треугольнике abc, сторона ac является именно прямой линией, так как она соединяет вершины a и c, и все точки этой стороны расположены на одной прямой.
Используя данную информацию, мы можем понять, что в треугольнике abc сторона ac является прямой линией, а также имеет длину 52.
Связь сторон в треугольнике abc: ac = 52
В треугольнике abc сторона ac может быть выражена числом 52. Связь между сторонами треугольника определяется его геометрическими свойствами. В данном случае, сторона ac имеет длину 52 единицы измерения.
Формула для нахождения длины прямой линии ac

В треугольнике abc с заданными сторонами a, b и c, где сторона ac равна 52, существует простая формула для нахождения длины прямой линии ac.
Используя теорему Пифагора, мы знаем, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Применяя эту теорему к треугольнику abc, мы можем записать формулу:
| ac2 = ab2 + bc2 |
Для нахождения длины прямой линии ac, мы можем подставить известные значения длин сторон ab и bc в данную формулу и вычислить значение ac.
В данном случае, зная что ac = 52, мы можем переписать формулу:
| 522 = ab2 + bc2 |
После проведения несложных вычислений, мы можем определить значения длин сторон ab и bc и решить задачу. В данном случае, значение ab и bc зависит от конкретных условий задачи.
Таким образом, используя формулу ac2 = ab2 + bc2 и известное значение длины ac, мы можем найти значения длин сторон ab и bc в треугольнике abc.
Определение связи сторон в треугольнике abc
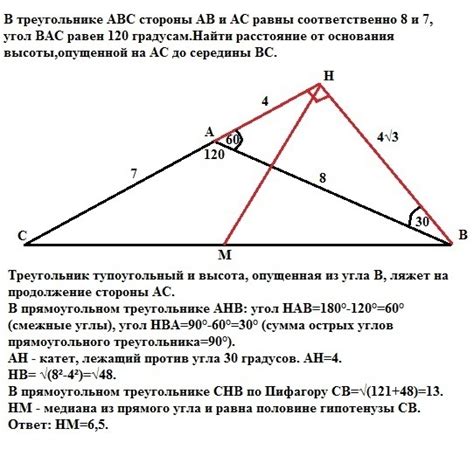
В треугольнике abc имеется связь между сторонами ac и bc.
Согласно заданному условию, длина стороны ac равна 52 единицам.
Связь между сторонами треугольника указывает на то, что сумма длин двух сторон треугольника всегда должна быть больше длины третьей стороны.
Таким образом, сумма длин сторон ac и bc должна быть больше длины стороны ab в треугольнике abc.
Для определения связи между другими сторонами треугольника abc необходимо знать их длины или иметь дополнительные условия.
Свойства и связи сторон в треугольнике
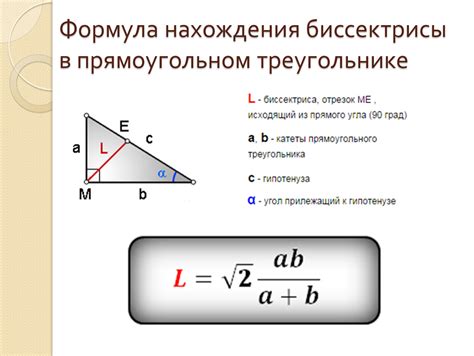
В треугольнике abc существует ряд свойств, связанных со сторонами данной фигуры. Одно из таких свойств представляет собой формулу, которая позволяет найти значение стороны ac в зависимости от других сторон треугольника:
ac = 52
Эта формула указывает на фиксированное значение стороны ac, которое равно 52. Таким образом, зная значения остальных сторон треугольника, можно вычислить значение стороны ac.
Кроме формулы, в треугольнике abc есть также особая связь между сторонами. Прямая линия, проведенная между точками a и c, образует гипотенузу прямоугольного треугольника, где сторона ac является наибольшей. Соответственно, сторона ac может быть также названа гипотенузой треугольника abc.
Знание этих свойств и связей сторон в треугольнике помогает не только в вычислении значений сторон, но и в определении свойств и характеристик самой фигуры. Треугольник является одной из важнейших геометрических фигур, и понимание его особенностей позволяет решать различные геометрические задачи и проблемы.
Значение длины стороны ac в треугольнике abc
В треугольнике abc прямая линия ac соединяет вершины a и c. Она является наибольшей стороной треугольника и служит основой для рассчета других параметров и свойств.
| Сторона | Длина |
|---|---|
| ab | ? |
| bc | ? |
| ac | 52 |
Длина стороны ac играет важную роль при решении различных задач, а также в формулах и теоремах, связанных с треугольником abc.
Взаимосвязи сторон треугольника abc и их значения

В треугольнике abc сторона ac имеет длину 52 единицы. Зная значение одной стороны, можно найти другие стороны треугольника, используя соответствующие геометрические связи.
Например, можно использовать теорему Пифагора для нахождения длины стороны ab или bc. Если известны длины двух сторон, то третью сторону можно найти с помощью неравенства треугольника.
Также, имея значение одной стороны, можно найти углы треугольника abc, используя тригонометрические связи. Например, с помощью теоремы синусов можно найти значения синусов углов треугольника abc и вычислить величины самих углов.
Зная значения сторон треугольника, можно также найти его площадь. Для этого можно использовать формулу Герона или формулу площади треугольника, основанную на полупериметре и радиусе вписанной окружности.
Таким образом, связи и значения сторон треугольника abc предоставляют много возможностей для нахождения значений других сторон и углов треугольника, а также вычисления его площади.



