Геометрия – один из древнейших разделов науки, изучающий пространственные фигуры, их свойства и взаимное расположение. Евклидова геометрия, основанная на аксиомах Евклида, была стандартной геометрией до XIX века.
Евклидова геометрия является абсолютной геометрией, то есть она применима к любому пространству. Ее аксиомы были разработаны Евклидом и оформлены в его труде "Начала". Евклидова геометрия основана на понятиях точек, прямых, плоскостей и тел, а также на операциях отрезания, равенства, совпадения и параллельности.
Однако неевклидовую геометрию, отличающуюся от евклидовой, разработали математики XIX века. Несмотря на отличия, неевклидова геометрия все же является геометрией и имеет свои аксиомы и систему рассуждений. Она исследует возможные альтернативы евклидовой геометрии, в которых одно или несколько ее аксиом не выполняются.
Наиболее известной ветвью неевклидовой геометрии является геометрия Лобачевского. В отличие от евклидовой геометрии, геометрия Лобачевского предполагает существование геометрических объектов, таких как геометрические фигуры, в которых сумма углов треугольника меньше 180 градусов. Это противоречит аксиоме Евклида о сумме углов треугольника, которая равна 180 градусов.
Таким образом, евклидова геометрия и неевклидова геометрия представляют собой две различные системы геометрических аксиом, изучающих пространство и его свойства. Евклидова геометрия является классическим примером абсолютной геометрии, тогда как неевклидова геометрия открывает возможности для существования альтернативных пространственных моделей.
Евклидова и неевклидова геометрия: основные отличия

Евклидова и неевклидова геометрия представляют собой два различных подхода к изучению пространства и его свойств. Давайте рассмотрим основные отличия между этими двумя геометрическими системами.
Евклидова геометрия, рассматриваемая в евклидовом пространстве, основывается на аксиомах Евклида и основных понятиях, таких как прямая, угол, треугольник и т.д. В евклидовой геометрии предполагается, что сумма углов треугольника равна 180 градусов, прямая можно продлить в бесконечность и тд. Это наиболее распространенный и знакомый нам тип геометрии, который мы изучаем в школе.
Однако существует и другой подход к геометрии, известный как неевклидова геометрия. Неевклидова геометрия была разработана в XIX веке Гауссом, Бельтрами и Лобачевским. Эти математики предложили новые модели геометрии, в которых отсутствуют некоторые основные аксиомы евклидовой геометрии.
Основное отличие между евклидовой и неевклидовой геометрией заключается в свойствах пространства. В неевклидовой геометрии сумма углов треугольника может быть больше или меньше 180 градусов, прямые линии могут быть ограниченными или закольцованными, а углы между параллельными линиями могут быть различными. Неевклидова геометрия не следует аксиомам, сформулированным Евклидом, и строит свои собственные геометрические основы.
Важно отметить, что неевклидова геометрия имеет свои приложения и применения, особенно в физике и науке о пространстве-времени. Теория относительности Эйнштейна базируется на неевклидовой геометрии и показывает, что пространство и время являются не статическими и взаимосвязанными.
Таким образом, евклидова и неевклидова геометрия отличаются друг от друга в своих основных принципах и свойствах пространства. Понимание этих различий позволяет математикам и физикам рассматривать пространство и его свойства с разных точек зрения и применять их в различных научных областях.
Принципы и аксиомы евклидовой геометрии
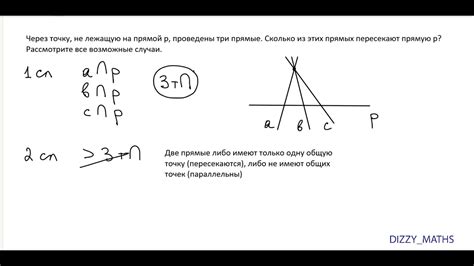
Вот некоторые из основных принципов и аксиом евклидовой геометрии:
- Аксиома 1: Между любыми двумя точками можно провести прямую линию.
- Аксиома 2: Любую линию можно продлить в обе стороны неограниченно.
- Аксиома 3: Из любой точки вне данной прямой можно провести единственную прямую, параллельную данной прямой.
- Аксиома 4: Все прямые углы равны друг другу.
- Аксиома 5: Через любые три точки, не лежащие на одной прямой, можно провести окружность, и центр окружности лежит на перпендикуляре к этой прямой, проходящем через середину отрезка, соединяющего две из этих точек.
- Аксиома 6: Все прямые углы, составленные одним и тем же переходящими прямыми и пересекающимися прямыми, равны друг другу.
- Аксиома 7: По заданной любой прямой и точке, не лежащей на этой прямой, можно провести только одну прямую, параллельную заданной прямой.
Эти принципы и аксиомы позволяют построить математическую систему, которая описывает геометрические объекты и отношения между ними. Евклидова геометрия широко применяется в физике, инженерии и других областях, где точность и простота используемых моделей являются ключевыми факторами.
Нарушение аксиом евклидовой геометрии

Первая аксиома - аксиома о двух точках - гласит, что через две различные точки всегда можно провести одну прямую. Но в неевклидовой геометрии, например, в геометрии Римана, пространство представляет собой сферу, а в некоторых точках сферы прямые ломаются или не пересекаются.
Вторая аксиома - аксиома о равенстве прямых - утверждает, что все прямые равны по длине. Однако в геометрии Лобачевского длина прямых может отличаться, в зависимости от положения в пространстве.
Третья аксиома - аксиома о треугольнике - утверждает, что сумма углов треугольника равна 180 градусов. В геометрии Лобачевского сумма углов треугольника может быть меньше 180 градусов, а в геометрии Римана - больше.
Четвертая аксиома - аксиома о параллельных прямых - гласит, что через внешнюю точку можно провести только одну прямую, параллельную данной. Но в геометрии Лобачевского существуют бесконечное число параллельных прямых, проходящих через данную точку.
Пятая аксиома - аксиома о расширении - утверждает, что две прямые, пересекаемые третьей, пересекаются между собой. В геометрии Лобачевского прямые, пересекающиеся с третьей, не обязательно пересекаются между собой.
Таким образом, неевклидова геометрия нарушает одну или несколько аксиом евклидовой геометрии, что приводит к возникновению новых геометрических систем, отличных от классической евклидовой геометрии.
Неевклидовы геометрии и их основные принципы

Одним из основных принципов неевклидовых геометрий является возможность существования бесконечного числа прямых параллельных данной прямой через заданную точку. В евклидовой геометрии, напротив, параллельная прямая единственна. Это приводит к тому, что в неевклидовых геометриях появляется несколько видов параллельных линий, которые взаимодействуют и могут пересекаться.
Другим принципом неевклидовых геометрий является принцип ограниченности площади треугольников на плоскости. В евклидовой геометрии площадь треугольника остается постоянной, независимо от размеров его сторон. В неевклидовых геометриях площадь треугольника может изменяться и зависит от его геометрических характеристик.
Одной из известных неевклидовых геометрий является сферическая геометрия, которая основана на трехмерной сфере. В сферической геометрии сумма углов треугольника превышает 180 градусов.
Другой известной неевклидовой геометрией является гиперболическая геометрия, которая основана на двумерной плоскости с отрицательной кривизной. В гиперболической геометрии сумма углов треугольника меньше 180 градусов.
Неевклидовы геометрии имеют много приложений в различных областях науки и техники, например, в теории относительности Альберта Эйнштейна. Изучение неевклидовых геометрий позволяет получить новые инсайты об особенностях пространства и расширяет наши представления о геометрии в широком смысле.
Практическое применение неевклидовых геометрий
Неевклидовые геометрии, в отличие от евклидовой геометрии, позволяют описывать пространства с нестандартными свойствами и структурами. Их практическое применение можно обнаружить в различных областях науки и техники.
Теоретическая физика: В физике неевклидовые геометрии применяются для описания космологических моделей, таких как модель Фридмана-Леметра-Робертсона-Уокера (FLRW). Эта модель описывает расширение Вселенной и использует неевклидовую геометрию для описания кривизны пространства.
Теория относительности: Альберт Эйнштейн в своей теории относительности использовал неевклидовую геометрию для описания кривизны пространства-времени. Это позволило объяснить гравитацию и движение планет и звезд вокруг больших масс, таких как Солнце или Черные дыры.
Геодезия и навигация: В геодезии и навигации неевклидовая геометрия используется для создания карт и навигационных систем, основанных на неевклидовых пространствах. Это позволяет то или иное картографирование, которое учитывает кривизну Земли и позволяет определить оптимальные пути и расстояния.
Теория информации: В теории информации неевклидовая геометрия используется для анализа и описания сложных сетей, таких как социальные сети и сети связей между веб-страницами. При использовании неевклидовых пространств возможно получение более точных и полных результатов анализа таких сетей.
Искусство и дизайн: Неевклидовая геометрия вдохновляет художников и дизайнеров создавать уникальные и необычные формы и структуры. Ее использование в искусстве позволяет создавать привлекательные и оригинальные произведения.
Криптография: Неевклидовая геометрия применяется в современной криптографии для защиты информации и шифрования данных. Ее использование позволяет создать более сложные и надежные криптографические системы, устойчивые к атакам.
Таким образом, неевклидовая геометрия имеет широкий спектр практического применения в различных научных и технических областях, от физики и геодезии до искусства и криптографии.



