Плоская произвольная система сил – это модель кинематики, которая используется для изучения уравновешенности и движения тел в плоскости. Она представляет собой математический аппарат, позволяющий описывать силы, действующие на различные объекты в плоской системе.
В плоской системе сил каждая сила представляется в виде вектора, имеющего определенные свойства, такие как направление, величина и точка приложения. Они могут быть представлены с использованием различных графических методов, например, с помощью векторных диаграмм или с использованием математических уравнений.
Плоская произвольная система сил имеет множество приложений в различных областях науки и техники. Она используется, например, в машиностроении для анализа механизмов и конструкций, в физике для изучения движения объектов и в строительстве для определения нагрузок на строительные элементы.
Основные понятия
При рассмотрении плоской произвольной системы сил важно учитывать следующие основные понятия:
Сила | Сила представляет собой физическую величину, обладающую как величиной, так и направлением. Она может действовать на тело, вызывая его перемещение или изменение состояния покоя. |
Система сил | Система сил - это совокупность двух или более сил, действующих на тело одновременно. В плоской произвольной системе сил две или более силы могут оказывать воздействие на одно или несколько тел, находящихся в одной плоскости. |
Сумма сил | Сумма сил - это результат взаимодействия всех сил в системе. Она может быть равной нулю, когда силы сбалансированы и действуют в разные стороны, или не равной нулю, когда силы неравны или действуют в одном направлении. |
Свойства плоской произвольной системы сил
1. Векторные свойства сил. Каждая сила в системе является векторной величиной, то есть имеет как величину, так и направление. Векторное сложение сил позволяет определить результатанту - силу, заменяющую всю систему.
2. Принцип суперпозиции. В плоской произвольной системе сил сумма векторов сил равна нулю. Это означает, что сумма всех сил, действующих в системе, равна нулевому вектору.
3. Принцип равнодействующей. В плоской системе сил сумма проекций сил на любую ось также равна нулю. Это означает, что сумма всех проекций сил на горизонтальную ось равна сумме проекций сил на вертикальную ось.
4. Эквивалентность систем. Две системы сил называются эквивалентными, если они создают одинаковую результатанту и одинаковую сумму их моментов относительно любой точки.
5. Условие равновесия. Система сил находится в состоянии равновесия, если результатанта равна нулевому вектору и сумма моментов сил относительно любой точки равна нулю.
6. Устойчивость равновесия. Равновесие системы сил может быть устойчивым или неустойчивым. Устойчивость зависит от положения центра тяжести и распределения сил в системе.
Понимание свойств плоской произвольной системы сил позволяет анализировать и решать разнообразные задачи механики. Знание этих свойств является важным фундаментом для изучения динамики твердого тела и других разделов физики.
Проекция сил на координатные оси
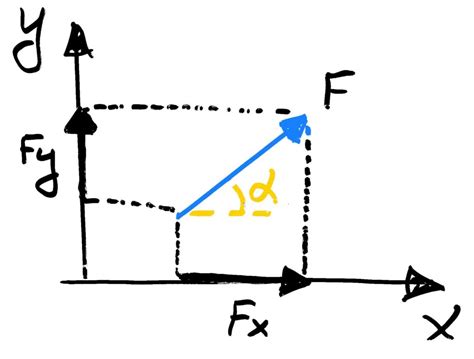
При анализе плоской произвольной системы сил важно определить, какова величина и направление каждой силы по отношению к координатным осям. Это позволяет установить, каким образом каждая сила влияет на движение или равновесие тела.
Проекция силы на ось определяется как проекция вектора силы на данную ось. Проекция можно выразить в виде скалярной величины.
Если сила направлена параллельно координатной оси, то проекция силы на эту ось равна величине самой силы. Если сила направлена перпендикулярно к координатной оси, то проекция будет равна нулю.
Проекция силы на ось может быть положительной или отрицательной в зависимости от направления силы. Если сила направлена в положительном направлении оси, то проекция будет положительной. Если сила направлена в отрицательном направлении оси, то проекция будет отрицательной.
Проекции сил на координатные оси могут быть использованы для составления уравнений равновесия или для вычисления суммарной проекции сил на ту или иную ось.
Пример:
Пусть имеется две силы, действующие на тело в плоскости xy. Сила F1 направлена вдоль оси x и имеет величину 10 Н, а сила F2 направлена вдоль оси y и имеет величину 5 Н. Проекции сил на оси x и y будут соответственно: F1x = 10 Н, F1y = 0 Н, F2x = 0 Н, F2y = 5 Н.
Проекция сил на координатные оси является важным инструментом в анализе плоских систем сил и позволяет более точно определить влияние каждой силы на тело.
Баланс сил в плоской системе
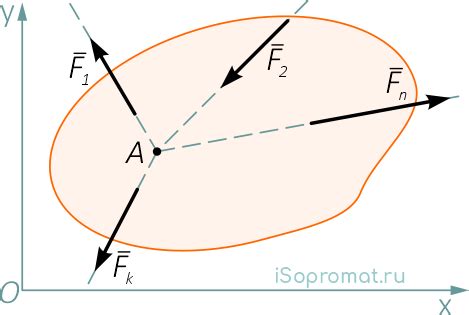
Баланс сил в плоской системе означает, что сумма всех сил, действующих на объект в плоскости, равна нулю. Это означает, что силы, действующие в различных направлениях, должны быть сбалансированы и не вызывать движения объекта.
Для определения баланса сил в плоской системе необходимо вычислить сумму всех проекций сил по каждой оси. Если сумма проекций сил по каждой оси равна нулю, то система сил сбалансирована.
Однако, если сумма проекций сил по каждой оси не равна нулю, то система сил несбалансирована. В этом случае, сила или силы, действующие в системе, будут вызывать движение объекта в определенном направлении.
Понимание баланса сил в плоской системе является важным элементом для анализа механических систем и предсказания их движения. Определение баланса сил позволяет определить, будет ли объект оставаться в состоянии покоя или приобретет ли он ускорение и начнет двигаться.
Примеры плоских произвольных систем сил
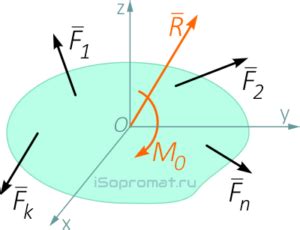
Вот несколько примеров плоских произвольных систем сил:
Веревка, натянутая между двумя точками. В этом случае сила натяжения в веревке будет действовать против направления растяжения веревки и будет направлена от одной точки к другой.
Система сил, действующих на тело, затянутое на наклонной плоскости. В этом случае сила тяжести будет направлена вниз, а сила нормальной реакции будет направлена вверх, перпендикулярно поверхности наклонной плоскости.
Две силы, действующие на тело в разных направлениях. В этом случае каждая сила будет действовать в определенном направлении, и их действие будет зависеть от их величины и угла между ними.
Это лишь некоторые примеры плоских произвольных систем сил. В реальности таких систем может быть множество, и для анализа их взаимодействия используются различные методы и модели.



