В математике максимум ─ это значение функции, которое является наибольшим среди всех значений функции в заданной области. Точка максимума, с другой стороны, представляет собой точку на графике функции, в которой функция достигает своего наибольшего значения.
Максимум функции может быть достигнут в нескольких точках, и эти точки будут являться точками максимума. Важно отметить, что значения функции во всех точках максимума будут одинаковыми и больше, чем значения во всех других точках области. Точка максимума ─ это координаты на графике функции, в которых функция достигает своего наибольшего значения.
Таким образом, разница между точкой максимума и максимумом функции заключается в том, что максимум функции это значение, а точка максимума это координаты на графике, в которых функция достигает этого самого максимума. Исследование максимумов функций играет важную роль в математическом анализе и помогает определять наилучшие решения в различных практических задачах.
Определение максимума функции
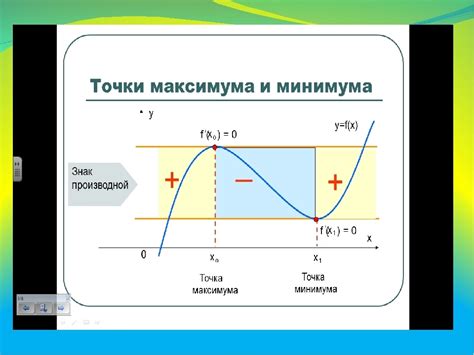
Для определения максимума функции, сначала нужно провести анализ дифференциала функции и найти все критические точки, где производная функции равна нулю или не существует. Затем, используя вторую производную, анализируются эти точки и определяется, является ли каждая из них максимумом, минимумом или точкой перегиба.
В таблице ниже представлено подробное описание критических точек и значений производных, чтобы определить максимум функции:
| Тип точки | Значение производной | Значение второй производной | Характеристика |
|---|---|---|---|
| Критическая точка | равна нулю | положительна | максимум |
| Критическая точка | равна нулю | отрицательна | минимум |
| Критическая точка | не существует | - | точка перегиба |
Свойства точки максимума функции
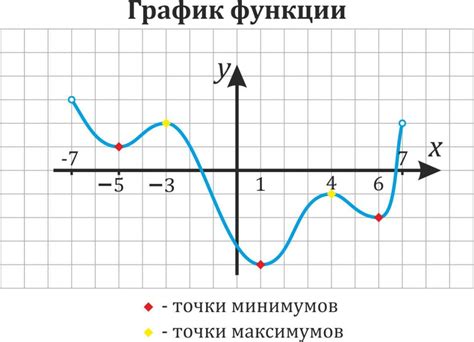
Основные свойства точки максимума функции включают:
- Значение функции: В точке максимума функция достигает своего наивысшего значения. Это значение может быть положительным, отрицательным или равным нулю в зависимости от характера функции.
- Первая производная: В точке максимума первая производная функции равна нулю. Это связано с тем, что точка максимума является местом изменения направления функции с возрастания на убывание.
- Вторая производная: В точке максимума вторая производная функции отрицательна. Это связано с тем, что в точке максимума функция имеет выпуклый характер, то есть кривизна функции направлена вниз.
Следуя этим свойствам, можно использовать их для определения точек максимума функции и анализа ее поведения. Определение точек максимума функции является важным шагом в решении различных задач, включая оптимизационные и определение границ допустимых значений.
Примечание: Важно помнить, что существует различные способы определения точек максимума функции, и эти свойства применимы только к определенным типам функций и условиям.
Определение точки максимума
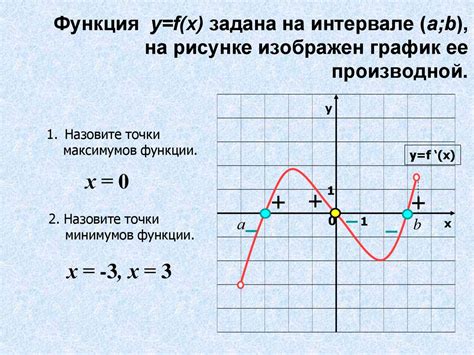
Для определения точки максимума функции, необходимо найти все критические точки, то есть точки, где производная функции равна нулю или не существует. Затем, с помощью второй производной, можно определить, является ли данная точка локальным максимумом или минимумом.
Если вторая производная отрицательна в критической точке, то функция имеет локальный максимум в этой точке. В случае если вторая производная положительна, функция имеет локальный минимум. Если же вторая производная равна нулю, тогда тест не даёт достоверного результата и может потребоваться дополнительное исследование функции.
Важно отметить, что точка максимума функции может быть либо локальной, то есть находиться в определенном интервале, либо глобальной, то есть являться наибольшим значением функции на всем ее домене. Для определения глобального максимума функции может использоваться графический метод или анализ поведения функции на бесконечности.
Свойства максимума функции

1. Уникальность
Максимум функции является единственным в заданной области определения. Это означает, что в любой другой точке функция будет принимать значения, меньшие, чем в точке максимума.
2. Локальность
Максимум функции может быть локальным, т.е. находиться внутри ограниченной области, или быть глобальным, т.е. охватывать всю область определения функции. Локальный максимум может иметь несколько точек, в которых значение функции достигает максимума, но глобальный максимум всегда единственен.
3. Определенность
Максимум функции всегда определен и существует, если функция непрерывна в заданной области определения. Это означает, что в данной области будет точно одна точка, в которой значение функции будет наибольшим.
4. Зависимость от области определения
Максимум функции может изменяться в зависимости от области определения. Для одной и той же функции максимумы могут быть разными в разных областях определения. Это связано с тем, что функция может иметь разные значения в разных областях определения.
Учет этих свойств максимума функции является важным при анализе функций и построении графиков. Они помогают понять, как функция ведет себя и находить экстремумы, в том числе максимумы, в заданной области определения.
Различия между точкой максимума и максимумом функции
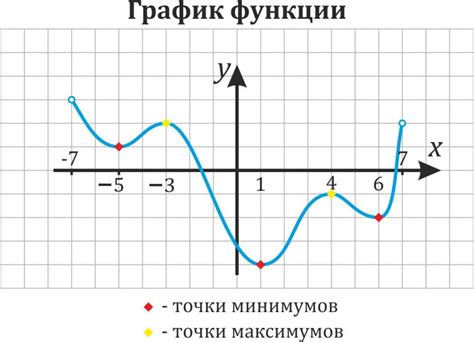
- Максимум функции: это наибольшее значение, которое может принимать функция на определенном промежутке или в области определения. Максимум функции может быть достигнут только в одной точке или может быть равным плюс бесконечности.
- Точка максимума: это значение аргумента функции, при котором функция достигает своего максимума. Точка максимума может быть одной или может быть несколькими, в зависимости от свойств функции.
Таким образом, различие между точкой максимума и максимумом функции заключается в том, что максимум функции - это само значение функции, а точка максимума - это значение аргумента функции, при котором она достигает своего максимума.
На практике, нахождение максимума функции может быть полезно, например, при оптимизации задач или анализе экстремальных значений. Точка максимума, в свою очередь, позволяет определить, при каких значениях аргумента функции достигается максимум.
Графическое представление точки максимума и максимума функции
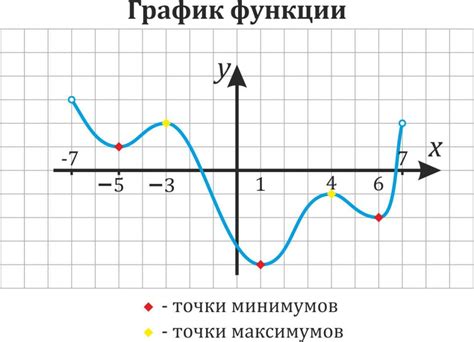
Точка максимума и максимум функции визуально отображаются на графике функции. График функции представляет собой точки, соединенные линиями, которые показывают зависимость функции от переменной.
Точка максимума на графике функции может быть определена как точка, в которой функция достигает наибольшего значения. В данной точке значение функции будет максимальным в заданном диапазоне значений переменной. Графически точка максимума будет выглядеть как вершина графика функции, находящаяся на наибольшей высоте.
Максимум функции представляет собой самое большое значение функции во всей области определения функции. Графическое представление максимума функции может быть представлено точкой, соответствующей точке максимума, или путем выделения на графике участка, где функция достигает своего максимального значения.
Определение точки максимума и максимума функции важно для анализа поведения функции и нахождения экстремальных значений. Она позволяет определить, насколько функция может изменяться и где она достигает своих наибольших значений. Графическое представление позволяет наглядно увидеть эти особенности функции и визуально анализировать ее поведение.
Примеры точек максимума и максимумов функций
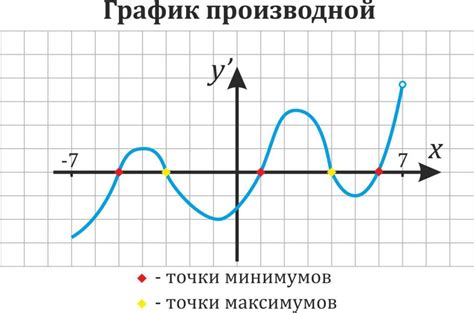
Пример точки максимума может быть найден на графике функции y = x^2. В этой функции точкой максимума будет вершина параболы, которая находится в точке (0, 0). Здесь функция достигает наибольшего значения и начинает убывать по обоим сторонам от этой точки.
Примером максимума функции может служить график функции y = sin(x) на интервале от 0 до π. В этой функции максимум функции равен 1 и достигается в точке x = π/2. Затем функция начинает убывать и достигает своего минимума в точке x = π.
Точка максимума и максимум функции имеют сходные концепции, но они отличаются. Точка максимума является конкретной точкой на графике функции, в то время как максимум функции - это значение, которое функция принимает на заданном интервале. Оба понятия играют важную роль в анализе функций и нахождении их экстремумов.
Точка максимума функции является конкретным значением аргумента, при котором функция достигает своего максимального значения. Она может быть найдена путем решения уравнения производной функции равной нулю. Точка максимума характеризуется координатами на графике функции.
Максимум функции представляет собой само значение функции в точке максимума. Это максимальное значение, которое может принимать функция на всей своей области определения. Максимум функции может быть найден путем подстановки значений аргументов в саму функцию или путем анализа графика функции.
Точка максимума и максимум функции являются важными концепциями в математике и используются в различных областях, таких как оптимизация, анализ данных и экономика. Понимание различий между этими понятиями позволяет более точно интерпретировать результаты и принимать обоснованные решения на основе математических моделей и функций.



