В математике понятия "ОДЗ" и "область определения функции" являются важными и тесно связанными. Они описывают множество значений, на которых функция определена, и помогают понять ее поведение и свойства.
ОДЗ, или область допустимых значений, определяет множество всех возможных аргументов функции, при которых она имеет смысл. То есть, это все те значения, которые можно подставить в функцию, чтобы получить корректный результат. ОДЗ может быть ограничено или неограничено, конечным или бесконечным множеством.
Область определения функции, с другой стороны, определяет все те значения, которые функция может принимать на своей области допустимых значений. Это множество всех значений, которые получаются при задании различных аргументов из ОДЗ в функцию.
Разница между ОДЗ и областью определения функции заключается в том, что ОДЗ определяет допустимые значения аргументов, а область определения определяет значения самой функции. То есть, ОДЗ говорит, где функция "работает", а область определения - какие значения она может принимать в этих точках.
Одз и область определения функции: принципы и отличия

Одз, или область допустимых значений, это множество всех возможных входных значений, на которых функция может быть определена. Она определяется ограничениями на значения аргументов функции, такими как условия, ограничения или другие факторы.
С другой стороны, область определения функции определяет множество всех возможных выходных значений, которые функция может принимать при заданных входных значениях. Она определяется правилами и формулами, по которым функция рассчитывает свои значения.
Важно отметить, что одз и область определения могут отличаться друг от друга. Например, функция может быть определена на всей числовой прямой, но иметь ограничения на допустимые значения, такие как неотрицательные числа или только целые числа. Это означает, что область определения функции будет состоять из допустимых значений, в то время как одз будет содержать все возможные значения из области определения.
Принципы определения одз и области определения основаны на понимании условий и правил функции. Отличия между ними состоят в том, что одз определяет все возможные входные значения, на которых функция может быть определена, в то время как область определения определяет все возможные выходные значения функции при заданных входных значениях.
Важно учитывать и принимать во внимание как одз, так и область определения при работе с функциями в математике и других областях науки, чтобы избежать неверных и некорректных результатов вычислений.
Одз: определение и примеры

Рассмотрим пример функции f(x) = √x. Одз для этой функции будет множество неотрицательных чисел, так как квадратный корень из отрицательного числа не существует. Таким образом, Одз для функции f(x) = √x будет [0, +∞).
Другим примером может служить функция g(x) = 1/x, где x ≠ 0 (x не равно нулю). В этом случае, Одз для функции g(x) будет множество всех чисел, кроме нуля. То есть, Одз для g(x) будет (-∞, 0) ∪ (0, +∞).
| Функция | Одз |
|---|---|
| f(x) = √x | [0, +∞) |
| g(x) = 1/x | (-∞, 0) ∪ (0, +∞) |
Важно помнить, что Одз может иметь различные формы и может зависеть от типа функции или конкретной задачи, решаемой с помощью функции. Одз нужно учитывать при определении допустимости значений аргументов функции и при анализе результатов, чтобы избежать ошибок и некорректных результатов.
Область определения функции: что это и как определить
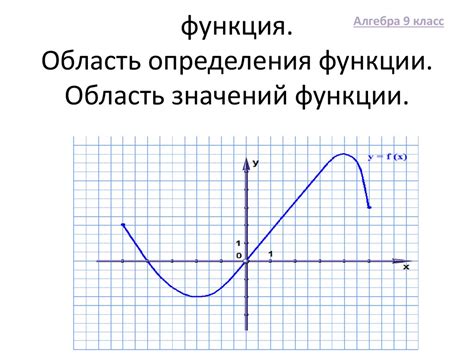
Для определения области определения функции необходимо учесть ее определение и ограничения, которые могут существовать.
Если функция определена аналитически, то область определения можно определить по следующим принципам:
| Тип функции | Область определения |
|---|---|
| Арифметическая функция | Все действительные числа |
| Логарифмическая функция | Только положительные числа |
| Тригонометрическая функция | Все действительные числа |
| Степенная функция | Зависит от показателя степени и основания |
Однако, не все функции можно определить аналитически. Например, функции, заданные графически или с помощью условия, могут иметь более сложные или ограниченные области определения. В таких случаях необходимо анализировать график функции или использовать математические методы, чтобы определить область определения.
Одз и область определения функции: особенности использования

Одз (область допустимых значений) и область определения функции играют важную роль в математике, а также в программировании и других областях, где функции широко используются. Хотя эти два понятия часто используются взаимозаменяемо, они имеют различия и особенности, о которых стоит знать.
Одз функции - это множество значений, которые функция может принимать на входе. Одз определяется ограничениями, накладываемыми на аргументы функции, такими как тип данных и домен значений. Одз функции может быть числовым, символьным или заранее заданным множеством значений.
Область определения функции - это множество значений, которые функция может принимать на выходе. Область определения зависит от характеристик самой функции и ее правил преобразования значений. Область определения может быть ограничена либо всем множеством допустимых значений, либо подмножеством Одз функции.
Одной из особенностей использования Одз и области определения функции является необходимость учитывать их значения при разработке алгоритмов программ и решении математических задач. Неправильный выбор Одз или неправильное определение области определения может привести к некорректным результатам или ошибкам выполнения программы.
Например, если функция принимает только положительные числа, то Одз будет положительным числовым множеством, а область определения будет множеством положительных и нулевых чисел.



