Синус и косинус - это два важных математических понятия, которые широко используются в различных областях науки и техники. Они относятся к так называемым тригонометрическим функциям и часто применяются для описания периодических явлений, таких как колебания и волны.
Основное отличие между синусом и косинусом заключается в их взаимосвязи с углом. Синус угла определяется как отношение противоположной стороны к гипотенузе, в то время как косинус угла - это отношение прилежащей стороны к гипотенузе. Иными словами, синус и косинус представляют собой соответствующие отношения сторон прямоугольного треугольника.
Синус и косинус обладают рядом важных свойств, которые делают их полезными для вычислений и моделирования. Например, они являются периодическими функциями, что означает, что они повторяются через определенный интервал. Кроме того, они могут быть использованы для представления гармонических колебаний и изменений резко изменяющихся значений со временем.
Различия синуса и косинуса
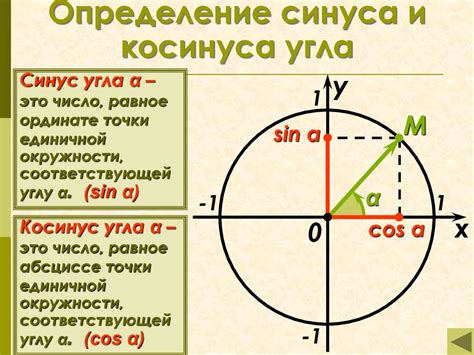
Первое отличие между синусом и косинусом заключается в их определениях. Синус угла определяется как отношение противоположной стороны треугольника к гипотенузе, в то время как косинус угла определяется как отношение прилежащей стороны треугольника к гипотенузе.
Второе отличие заключается в их значениях. Значение синуса всегда находится в диапазоне от -1 до 1, в то время как значение косинуса также находится в диапазоне от -1 до 1. Однако, значения синуса и косинуса различаются в зависимости от угла, и они имеют различные значения для разных углов.
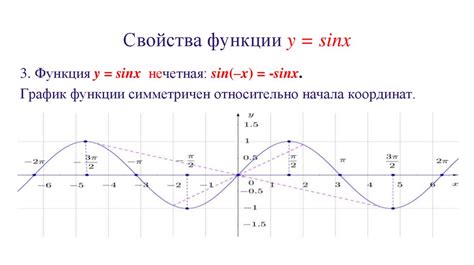
Следующее отличие между синусом и косинусом состоит в их графиках. График синуса имеет форму колебательной волны и является периодической функцией с периодом 2π. График косинуса также имеет форму колебательной волны и является периодической функцией с периодом 2π, но сдвинут относительно графика синуса на π/2.
В отличие от синуса, косинус является симметричной функцией относительно оси ординат. Это означает, что для каждого угла α, значение косинуса α равно значению косинуса (-α). В то же время, синус является несимметричной функцией, и его значение для угла α не равно значению синуса (-α).
Наконец, последнее отличие между синусом и косинусом заключается в их приложениях. В реальном мире синус и косинус широко используются для решения задач, связанных с колебаниями, звуком, электроникой, астрономией и много других областей. Однако, использование синуса и косинуса может различаться в зависимости от конкретной задачи или теории.
В итоге, синус и косинус являются важными функциями в математике и физике с различными свойствами и приложениями. Понимание их отличий может помочь в решении различных задач и в дальнейшем изучении более сложных математических и физических концепций.
Сравнение функций синуса и косинуса
Синус (sin) определяется как отношение противоположной стороны треугольника к гипотенузе, а косинус (cos) - как отношение прилежащей стороны к гипотенузе.
Основное отличие между синусом и косинусом заключается в фазе. Функция синуса достигает максимума в точке, где аргумент равен 90 градусам (или π/2 радиан), в то время как функция косинуса достигает максимума в точке, где аргумент равен 0 градусам (или 0 радиан).
Другое отличие между ними - это фазовая разность. Функция синуса имеет фазовую разность в 90 градусов (или π/2 радиан), по сравнению с функцией косинуса. То есть, когда значение синуса достигает максимума, значение косинуса находится в своем минимуме, и наоборот.
Обе функции являются периодическими, с периодом 2π радиан или 360 градусов. Это означает, что значения функций повторяются через каждые 2π радиан или 360 градусов. Они также являются четными функциями: синус(-x) = -sin(x) и косинус(-x) = cos(x).
Синус и косинус являются взаимосвязанными функциями, которые широко используются в различных областях науки и техники. Понимание их сходств и различий позволяет использовать их для решения разнообразных задач, связанных с изучением углов и треугольников.
Роль синуса и косинуса в тригонометрии

Синус угла в треугольнике определяется как отношение противолежащего катета к гипотенузе. Обозначается символом sin и записывается как sin(угол). Косинус угла в треугольнике определяется как отношение прилежащего катета к гипотенузе. Обозначается символом cos и записывается как cos(угол).
Синус и косинус имеют множество свойств и формул, которые позволяют вычислять их значения для различных углов. Эти функции используются в тригонометрических тождествах, которые позволяют связать значения синуса и косинуса для различных углов.
Одно из основных свойств синуса и косинуса - периодичность. Значения этих функций повторяются через определенные промежутки. Синус и косинус имеют период равный 360 градусам или 2π радианам. Это означает, что значения синуса и косинуса повторяются через каждые 360 градусов или 2π радианов.
Синус и косинус применяются в различных областях науки и техники. Они используются для описания и анализа колебательных процессов, таких как звуковые и световые волны. Также синус и косинус используются для решения задач геометрии, физики, инженерии и других областей науки.
| Угол (в градусах) | sin(угол) | cos(угол) |
|---|---|---|
| 0 | 0 | 1 |
| 30 | 0.5 | 0.866 |
| 45 | 0.707 | 0.707 |
| 60 | 0.866 | 0.5 |
| 90 | 1 | 0 |



