Математика окружает нас повсюду – она помогает нам решать задачи, считать, понимать мир. Как только мы научимся сложению, наш мозг открывает огромные возможности для вычислений. Почему сложение играет такую важную роль и как правильно его использовать, чтобы упростить вычисления?
Законы сложения – это основные правила, которые помогают нам проводить операции с числами. Когда мы складываем два числа, нам необходимо знать, как соединить их, чтобы получить правильный ответ. Законы сложения позволяют нам делать это правильно и без ошибок.
Первый закон сложения – это коммутативный закон. Согласно ему, порядок чисел не имеет значения при сложении: a + b = b + a. Например, 3 + 4 = 4 + 3. Это очень удобно, потому что мы можем менять местами слагаемые и получать такие же результаты. Также мы можем использовать этот закон для проверки наших вычислений – если мы поменяем местами числа и получим разные ответы, значит, где-то допущена ошибка.
Второй закон сложения – это ассоциативный закон. Согласно ему, при сложении трех или более чисел порядок их расстановки скобок не влияет на результат: (a + b) + c = a + (b + c). Например, (5 + 2) + 3 = 5 + (2 + 3). Этот закон позволяет нам отделять вычисления при сложении от порядка расстановки скобок и сокращает количество действий, которые нам необходимо выполнить.
Законы сложения
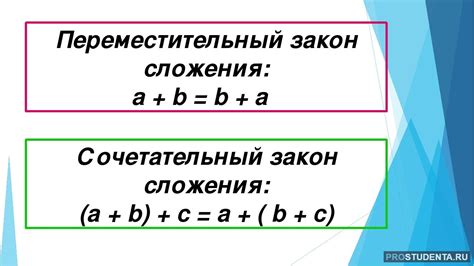
Основные законы сложения:
- Закон коммутативности. Согласно этому закону, порядок слагаемых не влияет на результат сложения. Например, для любых чисел а и b справедливо равенство: а + b = b + а.
- Закон ассоциативности. Закон данной операции говорит о том, что при сложении трех и более чисел их порядок можно менять, не меняя результата. Например, для любых чисел а, b и с выполняется равенство: (а + b) + с = а + (b + с).
- Закон нейтрального элемента. Этот закон обозначает существование такого числа, что его сложение с любым другим числом не меняет последнего. Данный элемент называют нейтральным или нулевым элементом. Например, для любого числа а выполняется равенство: а + 0 = а.
- Закон противоположного элемента. В соответствии с данным законом, любое число сложенное с его противоположным дает нейтральный элемент (ноль). Например, для любого числа а справедливо равенство: а + (-а) = 0.
Знание и применение законов сложения является важным аспектом в математике и находит свое применение в различных областях науки и техники. Они помогают сократить вычисления, упростить формулы и делают математические операции более удобными и понятными.
Законы сложения: основы и принципы
Законы сложения являются фундаментальными принципами, которые позволяют нам упростить вычисления и работу с математическими выражениями. Они основываются на простых, но важных математических свойствах, которые мы используем ежедневно. Понимание этих законов и их применение позволяют нам с легкостью решать задачи и проводить вычисления.
Погрузимся в основы и принципы законов сложения.
Закон коммутативности: этот закон гласит, что порядок слагаемых в сумме не важен, результат будет одинаковым. Например, если мы складываем числа a и b в порядке a + b, то результат будет таким же, как и при сложении чисел b и a, то есть b + a.
Закон ассоциативности: этот закон утверждает, что в сумме не важно, в каком порядке мы суммируем числа, результат останется неизменным. Если у нас есть числа a, b и c, то (a + b) + c будет равно a + (b + c).
Закон идентичности: по этому закону, сумма числа и нуля будет равна самому числу. Например, a + 0 = a.
Закон обратности: если мы складываем число с его отрицанием, то результат будет равен нулю. То есть a + (-a) = 0.
Законы сложения являются основой для решения более сложных математических задач. Они позволяют нам быть более гибкими и уверенными в вычислениях. Правильное применение этих законов помогает упростить математические выражения и рационально использовать ресурсы времени и усилий.
Помните, что правильное понимание и применение законов сложения являются важными навыками, которые рекомендуется освоить каждому, кто работает с математикой и вычислениями.
Ассоциативный закон сложения

Формально, ассоциативный закон сложения можно записать следующим образом:
(a + b) + c = a + (b + c)
где a, b и c - любые числа.
Например, рассмотрим следующие выражения:
1 + (2 + 3) = 1 + 5 = 6
(1 + 2) + 3 = 3 + 3 = 6
Как видно из примеров, порядок складывания чисел не влияет на итоговую сумму. Это позволяет нам упростить вычисления и изменять порядок складывания чисел для более удобного вычисления.
Ассоциативный закон сложения широко используется в математике и других областях, где применяются операции сложения. Он позволяет упростить многошаговые вычисления и сделать их более легкими для понимания.
Коммутативный закон сложения
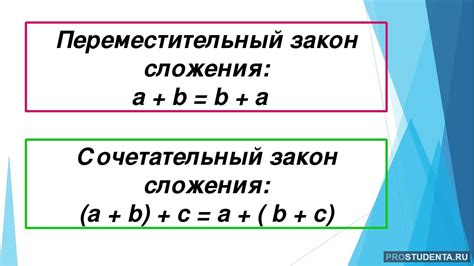
Например, для любых чисел а и b справедливо выражение: а + b = b + а.
Это означает, что можно менять местами слагаемые в сумме и при этом результат останется неизменным.
Коммутативный закон сложения особенно полезен при проведении вычислений, так как позволяет существенно упростить их. Например, при сложении нескольких чисел можно менять их порядок, не меняя при этом результата. Это позволяет выполнить вычисления более быстро и эффективно.
Нейтральный элемент сложения

В математике нейтральный элемент обозначается 0. При сложении чисел, если к любому числу прибавить 0, то результат останется неизменным. Например, 5 + 0 = 5. Это свойство действительно для любого числа, вне зависимости от его значения.
Таким образом, нейтральный элемент позволяет упростить вычисления. Вместо сложения самих чисел, можно просто добавить нулевой элемент, что существенно облегчает операции. Это особенно полезно при работе с большими числами или в сложных вычислениях, где каждая оптимизация важна.
Нейтральный элемент сложения также имеет важные свойства при выполнении других операций, таких как умножение и возведение в степень. Он может быть использован для определения других свойств числовых систем, а также для разработки математических моделей и алгоритмов.
Применение законов сложения в математике

Коммутативный закон сложения утверждает, что порядок слагаемых не влияет на результат. Это значит, что если мы сложим два числа в любом порядке, то получим тот же результат. Например, 2 + 3 равно 3 + 2, что равно 5.
Ассоциативный закон сложения гласит, что порядок выполнения сложения не влияет на результат. Это означает, что если у нас есть несколько слагаемых, то мы можем сначала сложить первые два, а затем сложить полученную сумму с третьим числом, и результат будет тем же, что и если бы мы сложили все числа вместе. Например, (2 + 3) + 4 равно 2 + (3 + 4), и оба равны 9.
Применение этих законов в математике позволяет упрощать вычисления. Например, если нам нужно сложить несколько чисел, мы можем выбрать любой порядок сложения, и результат будет одинаковым. Это может быть полезно, когда мы сталкиваемся с большими числами или сложными выражениями.
Также, применение законов сложения позволяет нам сгруппировать слагаемые по-разному, чтобы упростить вычисления. Например, если у нас есть выражение 2 + 3 + 4 + 5, мы можем сложить 2 с 3, а затем сложить 4 с 5, а затем сложить полученные суммы. Таким образом, мы можем разделить сложную задачу на более простые действия.
Законы сложения не только упрощают вычисления, но и помогают развивать логическое мышление и абстрактное мышление. Использование этих законов помогает нам анализировать и решать сложные математические проблемы.
Итак, применение законов сложения в математике позволяет нам упростить вычисления, сгруппировав слагаемые по-разному, и развивает наше логическое и абстрактное мышление. Они являются неотъемлемой частью математики и помогают нам понять и решать сложные задачи.
Упрощение вычислений с помощью законов сложения
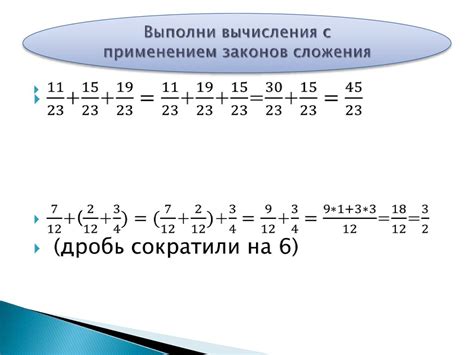
Один из наиболее известных законов сложения - ассоциативный закон, который гласит, что при сложении трех и более чисел порядок скобок не имеет значения. Это позволяет нам переставлять и группировать числа в выражениях так, чтобы упростить их вычисление.
Также существует коммутативный закон сложения, согласно которому порядок слагаемых не влияет на сумму. Это позволяет нам менять порядок чисел в выражениях без изменения результата.
Сочетание этих двух законов сложения позволяет существенно упростить вычисления и сделать их более легкими и понятными. Они помогают снизить количество шагов и операций, что особенно важно при работе с большими и сложными выражениями.
Законы сложения являются важным инструментом в математике и имеют широкое применение в различных областях, включая алгебру, физику и экономику. Понимание и использование этих законов позволяет значительно ускорить и упростить вычисления, что делает их незаменимыми в решении различных задач.
Законы сложения и преобразования выражений

Первый закон сложения - закон коммутативности: порядок слагаемых не влияет на сумму. Другими словами, можно менять местами слагаемые и получить одинаковый результат. Например, выражение 2 + 3 + 4 равно 9, и также равно 4 + 3 + 2.
Второй закон сложения - закон ассоциативности: способ группировки слагаемых не влияет на сумму. Это значит, что можно складывать слагаемые в любом порядке, не меняя результат. Например, выражение (2 + 3) + 4 равно 9, и также равно 2 + (3 + 4).
Третий закон сложения - закон противоположности: любое число при сложении с противоположным числом дает ноль. Противоположное число - это число, противоположное по знаку, но с тем же по абсолютной величине. Например, если сложить число 5 и число -5, получится 0.
Знание этих законов поможет упростить вычисления и выполнить сложение чисел более эффективно. Они являются основой для решения различных задач в алгебре и математическом анализе.
Примеры применения законов сложения

Пример 1:
Дано выражение a + (b + c).
В соответствии со законом ассоциативности сложения, можно изменить порядок скобок:
(a + b) + c.
Это позволяет упростить расчеты и сделать выражение более читаемым.
Пример 2:
Рассмотрим выражение 5 + 6 + 7.
Согласно закону коммутативности сложения, можно изменить порядок слагаемых:
7 + 5 + 6.
Это не меняет результата вычисления, но может сделать его более удобным для выполнения.
Пример 3:
Предположим, у нас есть выражение (a + b) + c и мы знаем значения a, b и c.
В соответствии с законом сложения чисел, мы можем сначала сложить значения внутри скобок:
a + b = d, где d - новая переменная.
Теперь выражение может быть переписано как d + c.
Это упрощает вычисления и позволяет избежать повторных операций.
Применение законов сложения может значительно упростить вычисления и сделать их более быстрыми и понятными. Понимание этих законов позволяет математикам и студентам применять их в различных задачах и ситуациях, включая алгебру, геометрию и другие области математики.
Законы сложения и их роль в алгебре

Первым и основным законом сложения является ассоциативный закон. Он гласит, что порядок расстановки скобок не влияет на результат сложения. Например, если у нас есть выражение (а + b) + c, то его результат будет таким же, как и у выражения а + (b + c). Такой закон позволяет группировать слагаемые и менять их порядок без изменения суммы.
Вторым законом сложения является коммутативный закон. Он говорит о том, что порядок слагаемых не важен при сложении. Например, 2 + 3 будет равно 3 + 2. Этот закон позволяет быстро и удобно менять местами слагаемые, что упрощает вычисления.
Следующим законом сложения является нулевой элемент. Он утверждает, что сумма числа и нуля равна самому числу. Например, 5 + 0 будет равно 5. Этот закон позволяет упрощать выражения, если одно из слагаемых равно нулю.
Также существует обратный элемент, или закон обратности. Он гласит, что к каждому числу существует противоположное число, сумма которого с исходным числом равна нулю. Например, для числа 4 его обратным элементом будет -4, так как 4 + (-4) равно 0. Этот закон позволяет изменять знаки слагаемых и упрощать выражения.
Законы сложения играют важную роль в алгебре, поскольку позволяют совершать преобразования выражений, упрощать их и находить более эффективные способы вычислений. Знание этих законов помогает более глубоко понять принципы алгебраических операций и применять их в решении задач различной сложности.




