Углы в прямоугольнике являются одним из основных элементов геометрии, их понимание позволяет выполнять различные математические операции и решать задачи. Изучение углов в прямоугольнике поможет вам лучше понять его свойства и особенности.
Прямоугольник - это четырехугольник, у которого все углы прямые (равны 90 градусов). Углы в прямоугольнике обладают рядом важных свойств:
- Сумма всех углов в прямоугольнике равна 360 градусов. Это следует из того, что вся окружность составлена из 4 прямоугольников (4 * 90 = 360).
- Противоположные углы в прямоугольнике равны друг другу. Например, если один угол прямоугольника равен 45 градусам, то второй противоположный угол также будет равняться 45 градусам.
- Дополнительные углы в прямоугольнике равны 90 градусам. Например, если угол прямоугольника равен 30 градусам, то его дополнительный угол будет равняться 90 - 30 = 60 градусов.
Для расчета углов в прямоугольнике можно использовать формулу:
сумма углов в прямоугольнике = 360 градусов
При известных значениях одного из углов можно легко найти значение остальных углов, используя указанную формулу.
Что такое углы в прямоугольнике
Углы в прямоугольнике имеют несколько свойств:
- Все углы прямоугольника равны между собой и равны 90 градусам.
- Сумма всех углов прямоугольника равна 360 градусам.
- Противоположные углы прямоугольника равны между собой.
- Боковые углы прямоугольника смежны и дополняют друг друга до 90 градусов.
Углы в прямоугольниках играют важную роль в геометрии. Они используются для определения свойств прямоугольников и являются базовым понятием для изучения других фигур и форм. Знание углов в прямоугольниках позволяет решать задачи связанные с площадью, периметром и другими характеристиками прямоугольников.
Формула для расчета углов в прямоугольнике

В прямоугольнике существуют четыре угла, из которых два противоположных угла равны друг другу. Формула для расчета углов в прямоугольнике основана на том, что сумма всех углов в прямоугольнике равна 360 градусов.
Для расчета каждого угла в прямоугольнике можно использовать следующую формулу:
| Угол | Формула |
|---|---|
| Угол 1 | Угол 1 = 180 - Угол 2 |
| Угол 2 | Угол 2 = 180 - Угол 1 |
| Угол 3 | Угол 3 = 180 - Угол 4 |
| Угол 4 | Угол 4 = 180 - Угол 3 |
Пример расчета углов в прямоугольнике:
| Угол | Формула | Результат |
|---|---|---|
| Угол 1 | Угол 1 = 180 - Угол 2 | Угол 1 = 180 - 90 = 90 градусов |
| Угол 2 | Угол 2 = 180 - Угол 1 | Угол 2 = 180 - 90 = 90 градусов |
| Угол 3 | Угол 3 = 180 - Угол 4 | Угол 3 = 180 - 90 = 90 градусов |
| Угол 4 | Угол 4 = 180 - Угол 3 | Угол 4 = 180 - 90 = 90 градусов |
Таким образом, в прямоугольнике все углы равны между собой и составляют 90 градусов каждый.
Примеры расчета углов в прямоугольнике

Углы в прямоугольнике могут быть вычислены с использованием простых геометрических формул. Для этого нам нужно знать длины сторон прямоугольника.
Рассмотрим пример. Предположим, что у нас есть прямоугольник, у которого одна сторона равна 5 см, а другая сторона равна 10 см.
Для вычисления углов воспользуемся следующими формулами:
Угол A = arctg(b/a)
Угол B = 90° - A
Где a - длина первой стороны прямоугольника, b - длина второй стороны прямоугольника.
Подставим значения из примера:
a = 5 см
b = 10 см
Вычислим углы:
Угол A = arctg(10/5) = arctg(2) ≈ 63.4°
Угол B = 90° - 63.4° ≈ 26.6°
Таким образом, в нашем прямоугольнике угол A составляет примерно 63.4°, а угол B - примерно 26.6°.
Зная длины сторон прямоугольника, можно легко вычислить углы, что облегчает работу с данным геометрическим объектом.
Равные углы в прямоугольнике
Например, если известно, что один из углов прямоугольника равен 90 градусов, то автоматически становится известным и значение всех остальных углов. Все углы в прямоугольнике равны 90 градусов.
Также можно использовать свойство равности углов для нахождения значений углов, если известны некоторые другие углы. Например, если в прямоугольнике два угла равны между собой, то остальные два угла также будут равными.
Однако стоит помнить, что это свойство работает только в прямоугольниках. В других четырехугольниках равные углы не гарантируются.
Острые углы в прямоугольнике
Острыми углами в прямотугольнике называются углы, которые меньше прямого угла и больше нуля градусов. В прямоугольнике всегда 4 острых угла.
Зная значения двух острых углов, можно легко вычислить значения остальных двух. Так как сумма углов прямоугольника равна 360 градусам, сумма мер острых углов будет равна 180 градусам.
Допустим, у нас есть прямоугольник, в котором один острый угол равен 30 градусам. Тогда, для того чтобы найти величины остальных трех углов, необходимо от общей суммы острого угла вычесть изначально заданный угол и разделить полученную разницу на 3. В нашем случае: (180 - 30) / 3 = 50 градусов.
| Угол | Величина, градусы |
|---|---|
| Прямой угол | 90 |
| Острый угол 1 | 30 |
| Острый угол 2 | 50 |
| Острый угол 3 | 50 |
В таблице представлены значения углов для примера, где один из острых углов равен 30 градусам.
Зная значения всех углов в прямоугольнике, можно рассчитать различные параметры, например, длины сторон и диагоналей.
Тупые углы в прямоугольнике
Прямоугольник имеет четыре угла. Все углы, кроме одного, называются острыми, а один угол называется тупым. Тупым углом в прямоугольнике считается угол, который больше 90 градусов.
Чтобы найти тупой угол в прямоугольнике, необходимо знать значения всех острых углов. Формула для расчета тупого угла в прямоугольнике выглядит следующим образом:
Тупой угол = 360 градусов - сумма всех острых углов
Например, если значения острых углов в прямоугольнике равны 60°, 70° и 80°, то тупой угол будет равен:
Тупой угол = 360 градусов - (60 градусов + 70 градусов + 80 градусов) = 150 градусов
Таким образом, в прямоугольнике с острыми углами 60°, 70° и 80° имеется один тупой угол, который равен 150 градусов.
Как определить углы в прямоугольнике по длинам сторон
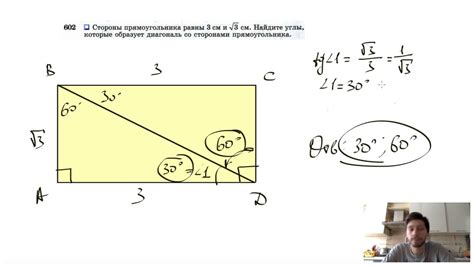
Для расчета углов в прямоугольнике, мы можем использовать обратные тригонометрические функции - арктангенс, арксинус и арккосинус. Воспользуемся соотношениями:
Угол A = arctan(b/a)
Угол B = arcsin(b/c)
Угол C = arccos(a/c)
Где а и b - длины сторон прямоугольника, а c - диагональ прямоугольника.
Например, если длина одной стороны прямоугольника равна 6 см, а длина другой стороны - 8 см, то можно рассчитать углы следующим образом:
Угол A = arctan(8/6) ≈ 53.13 градусов
Угол B = arcsin(6/10) ≈ 36.87 градусов
Угол C = arccos(8/10) ≈ 36.87 градусов
Таким образом, угол A будет примерно равным 53.13 градусов, угол B и угол C будут примерно равны 36.87 градусов.
Эти формулы позволяют определить углы прямоугольника на основе длин его сторон и являются полезными в геометрии и инженерных расчетах.
Взаимосвязь между углами и сторонами в прямоугольнике
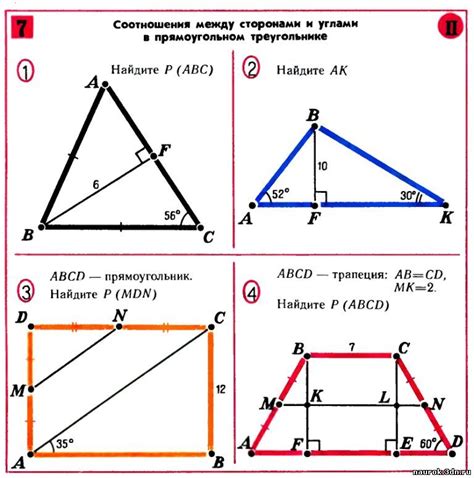
В прямоугольнике есть две основных формулы, описывающих связь между углами и сторонами:
| Формула | Описание |
|---|---|
| Сумма углов прямоугольника | В сумме все углы прямоугольника равны 360 градусам. |
| Формула угла в прямоугольнике | Угол в прямоугольнике определяется соотношением между сторонами. Для прямоугольника с длинной стороной а и короткой стороной b, синус угла равен отношению b к а, а косинус угла равен отношению а к b. |
Например, если в прямоугольнике длина одной стороны равна 5, а длина другой стороны равна 8, то можно рассчитать значения синуса и косинуса угла в этом прямоугольнике. Синус угла будет равен 5/8, а косинус угла будет равен 8/5.
Знание взаимосвязи между углами и сторонами в прямоугольнике позволяет решать различные задачи, связанные с его геометрией, например, находить значения углов по заданным сторонам или находить значения сторон по заданным углам.
Значение углов в прямоугольнике для построения фигур
Углы в прямоугольнике играют важную роль при построении различных геометрических фигур. Зная значения углов, мы можем определить форму и размеры этих фигур.
В прямоугольнике все углы равны 90 градусам. Это означает, что все четыре угла прямоугольника являются прямыми углами. Благодаря этому свойству прямоугольник может быть использован для построения других фигур.
Например, если мы возьмем два прямоугольника одинакового размера и поставим их друг на друга так, чтобы углы совпадали, мы получим квадрат. Квадрат имеет все стороны и углы равными между собой.
Еще одним примером использования углов прямоугольника является построение треугольников. Если мы возьмем одну сторону прямоугольника и соединим ее с противоположной вершиной прямоугольника, то получим треугольник. Значение угла в этом треугольнике будет равно 90 градусам, так как одна сторона будет прямой угол.
Таким образом, значение углов в прямоугольнике является важным инструментом для построения различных фигур. Оно помогает определить форму и размеры фигур, а также может использоваться для решения геометрических задач.



