Умение правильно корректировать и развивать свои навыки - это одна из самых важных навыков для достижения успеха в жизни. Однако, не всегда понять, как именно улучшить свои навыки, бывает просто. Понятие ряда - это инструмент, который может помочь нам эффективно усваивать и развивать новые навыки.
Ряд представляет собой последовательность действий, которые мы выполняем, чтобы достичь определенной цели. Каждое действие в ряду имеет свою важность и вкладывает в наши навыки какую-то часть информации. Осознавая этот принцип, мы можем структурировать наши усилия и сделать процесс развития навыков более систематическим и эффективным.
Усвоение понятия ряда позволяет нам не только понять, как именно формируются навыки, но и увидеть, что каждый шаг в этом процессе имеет свою ценность. Зачастую мы сосредотачиваемся только на конечной цели и не обращаем внимания на промежуточные шаги. Однако именно в этих шагах заключается ключ к успешной коррекции навыков и их качественному усвоению.
Раздел 1. Первое знакомство с понятием ряда

Первое знакомство с понятием ряда начинается с изучения его определения. Определение ряда состоит из двух частей: первой и второй. В первой части определяется общий вид слагаемых, а во второй – основная цель ряда.
Для начала необходимо разобраться с терминологией. Слагаемое – это каждое отдельное число или выражение, входящее в ряд. Элементы ряда обозначаются как a1, a2, a3, ..., an. Здесь n – число слагаемых в ряду. Например, a1 + a2 + a3 + ... + a10 - это ряд с 10 слагаемыми.
Во второй части определения ряда задается его цель – найти сумму бесконечного числа слагаемых. Если такая сумма существует и конечна, то ряд называют сходящимся. В противном случае ряд называется расходящимся.
Для наглядности и удобства изучения ряда, можно представить его в виде таблицы. Ниже приведен пример таблицы, в которой представлены первые 5 слагаемых ряда:
| Номер слагаемого (n) | Слагаемое (an) |
|---|---|
| 1 | a1 |
| 2 | a2 |
| 3 | a3 |
| 4 | a4 |
| 5 | a5 |
Таким образом, первое знакомство с понятием ряда заключается в изучении его определения, терминологии и представлении слагаемых в виде таблицы. Понимание этих основных понятий и методов представления поможет в последующих шагах изучения и усвоения данной темы.
Понятие ряда и его важность

Ряд может быть представлен в различных областях жизни и деятельности. Например, в математике ряд используется для представления бесконечной суммы чисел или элементов. В музыке ряд нот может образовывать определенную мелодию или аккорд. В учебном процессе ряды могут использоваться для представления последовательности задач или упражнений.
Усвоение понятия ряда имеет важное значение для успешной коррекции навыков. Понимая ряд, можно упорядочить и систематизировать новую информацию или навыки, что способствует их успешному усвоению и коррекции.
Понятие ряда может помочь в постановке целей и контроле за успешностью коррекции навыков. Представление навыков в виде ряда поможет определить, на каком этапе находится исправление неправильных действий и как продвигается процесс коррекции.
В обучении и воспитании понятие ряда является полезным инструментом для педагогов и специалистов по коррекции навыков. Развитие понятия ряда у детей и взрослых способствует формированию логического мышления и умения структурировать информацию. Подобное умение не только помогает в коррекции навыков, но и в разных сферах жизни – от организации работы до разрешения конфликтов.
Основные типы рядов

В математике существует несколько основных типов рядов, которые играют важную роль в усвоении понятия ряда и коррекции навыков. Рассмотрим их подробнее:
| Арифметический ряд | Арифметический ряд представляет собой сумму членов, в котором каждый следующий член получается прибавлением или вычитанием одной и той же фиксированной величины. Формула арифметического ряда: Sn = a + (a + d) + (a + 2d) + ... + (a + (n-1)d), где Sn - сумма первых n членов, a - первый член, d - разность между соседними членами. |
| Геометрический ряд | Геометрический ряд представляет собой сумму членов, в котором каждый следующий член получается умножением или делением предыдущего члена на одно и то же число (называемое знаменателем). Формула геометрического ряда: Sn = a + aq + aq^2 + ... + aq^(n-1), где Sn - сумма первых n членов, a - первый член, q - знаменатель. |
| Абсолютно сходящийся ряд | Абсолютно сходящийся ряд – это ряд, сходящийся абсолютно для любого упорядочивания его членов. В математике сходимость ряда подразделяют на абсолютную и условную. Абсолютно сходящийся ряд сохраняет свою сходимость при изменении порядка его членов. |
Знание основных типов рядов позволяет лучше понять принципы и свойства рядов, а также правильно применять методы их коррекции в образовательном процессе.
Раздел 2. Коррекция навыков через понимание ряда

Понимание ряда позволяет выявить закономерности и особенности образования элементов в последовательности, что в свою очередь помогает эффективно корректировать навыки. При анализе ряда мы можем определить его общую формулу или закономерность, а также выявить регулярные шаги между элементами.
| Тип ряда | Описание | Пример |
|---|---|---|
| Числовой ряд | Ряд, состоящий из числовых элементов. | 1, 2, 3, 4, 5, 6, 7, ... |
| Геометрический ряд | Ряд, в котором каждый последующий элемент получается умножением предыдущего элемента на постоянное число. | 2, 4, 8, 16, 32, 64, ... |
| Арифметическая прогрессия | Ряд, в котором каждый последующий элемент получается путем добавления постоянного числа к предыдущему элементу. | 3, 6, 9, 12, 15, ... |
| Паттерн-ряд | Ряд, в котором элементы образуют определенный паттерн или последовательность. | A, B, C, D, E, F, ... |
Понимание особенностей ряда позволяет нам определить правила и логику, на основе которых строится последовательность элементов. Это важно для коррекции навыков, так как понимание ряда помогает нам прогнозировать следующие шаги и принимать правильные решения при решении задач и преодолении трудностей. Поэтому осознанное усвоение понятия ряда является необходимым инструментом для успешной коррекции навыков.
Как ряды помогают выявить ошибки
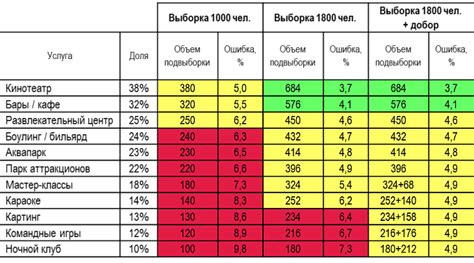
Ряды позволяют провести детальный анализ различных аспектов навыка. Например, если речь идет о развитии математических навыков, то можно составить ряды, отражающие уровень правильных ответов ученика по времени или по сложности задач. Анализ этих рядов позволяет выявить, на каких этапах ученик испытывает наибольшие трудности и совершает наибольшее количество ошибок.
Для выявления ошибок в письменном проявлении навыков можно использовать ряды, отражающие количество синтаксических и грамматических ошибок в текстах ученика. Также можно использовать ряды, отслеживающие различные метрики, такие как сложность слов, длина предложений и т.д. Анализ этих рядов позволяет определить, в каких областях ученику необходима коррекция и дополнительная поддержка.
Ряды также позволяют выявить прогресс и успехи ученика. Сравнивая повторные ряды с начальными показателями, можно определить, какие ошибки устранены, какие навыки улучшены и где нужно продолжать работу.
В целом, ряды играют важную роль в процессе коррекции навыков, позволяя выявить ошибки, определить области для развития и отслеживать прогресс ученика. Используя ряды, педагоги и специалисты могут более эффективно работать над коррекцией различных навыков и обеспечить успешное усвоение понятия ряда у учеников.



