Уравнение зависимости координаты от времени - это математическое выражение, которое описывает движение объекта в пространстве в зависимости от прошедшего времени. Это основной инструмент в физике для изучения и анализа движения тел.
Уравнение зависимости координаты от времени может быть либо аналитическим, либо численным. Аналитическое уравнение является точным математическим выражением, которое позволяет определить координату объекта в любой момент времени. Численное уравнение, в свою очередь, использует методы аппроксимации и приближения для вычисления координаты объекта в конкретные моменты времени.
Уравнение зависимости координаты от времени может иметь различные формы в зависимости от характеристик движения объекта. Например, для прямолинейного равномерного движения уравнение может иметь вид x = v * t, где x - координата объекта, v - скорость, t - время. Для движения с постоянным ускорением уравнение будет иметь более сложный вид.
Важно отметить, что уравнение зависимости координаты от времени является лишь математическим описанием движения, а не физическим объяснением причин и механизмов движения объекта. Для полного понимания движения необходимо учитывать и другие факторы, такие как сила, масса и воздействия других тел.
Определение уравнения зависимости координаты от времени
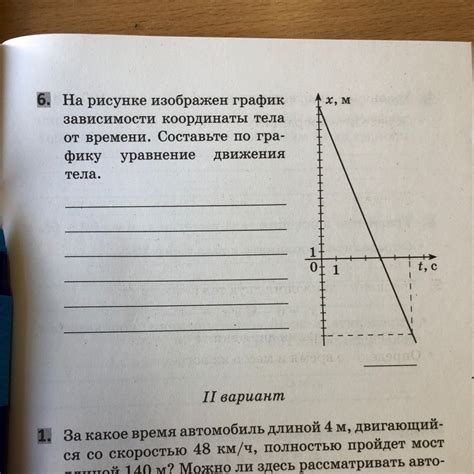
В классической механике уравнение зависимости координаты от времени обычно записывается в виде:
x(t) = x₀ + v₀t + (1/2)at²
где:
- x(t) - координата объекта в момент времени t
- x₀ - начальная координата объекта
- v₀ - начальная скорость объекта
- a - ускорение объекта
- t - время
Уравнение содержит все необходимые параметры для описания движения объекта: начальное положение, начальную скорость и ускорение. Путем подстановки значений этих параметров и времени в уравнение, можно определить координату объекта в любой момент времени.
Уравнение зависимости координаты от времени широко используется в физике, инженерии и других науках для моделирования движения объектов и предсказания их положения в будущем или прошлом.
Физический смысл уравнения зависимости координаты от времени

Уравнение зависимости координаты от времени может иметь различные формы в зависимости от характера движения. Например, для равномерного прямолинейного движения уравнение имеет простую форму: x = x0 + vt, где x - координата в момент времени t, x0 - начальная координата, v - скорость движения.
Для сложных форм движения, таких как движение с постоянным ускорением или гармоническое движение, уравнение может быть более сложным и содержать дополнительные параметры.
Зная уравнение зависимости координаты от времени, можно определить, как изменяется положение тела во времени и прогнозировать его будущее положение. Это позволяет решать различные задачи, такие как определение траектории движения, вычисление времени достижения определенной точки, определение скорости и ускорения.
Физический смысл уравнения зависимости координаты от времени – это мощный инструмент для исследования и объяснения различных физических явлений, позволяющий установить закономерности и предсказывать результаты экспериментов.
Примеры уравнений зависимости координаты от времени в различных областях науки
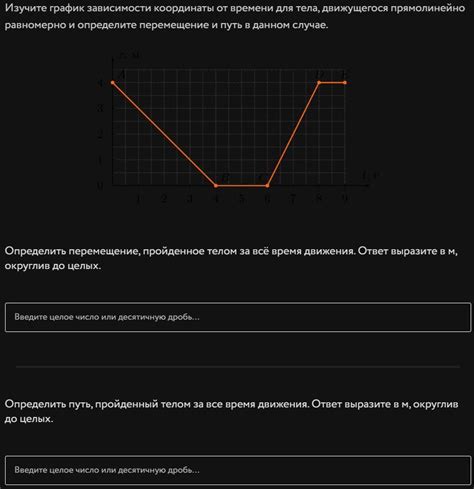
1. Механика:
- Уравнение движения прямолинейно движущегося тела без ускорения: x(t) = x0 + vt
- Уравнение движения тела под действием постоянной силы: x(t) = x0 + v0t + (1/2)at^2
- Уравнение колебательного движения маятника: x(t) = A*cos(ωt + φ)
2. Электродинамика:
- Уравнение распространения электромагнитной волны в вакууме: E(x, t) = E0*sin(kx - ωt)
3. Квантовая механика:
- Уравнение Шредингера для частицы в потенциальной яме: Ψ(x, t) = Ψ0*sin(kx - ωt)
4. Динамика популяций:
- Уравнение экспоненциального роста популяции: N(t) = N0*e^(rt)
- Уравнение Логистической модели роста популяции: N(t) = K / (1 + (K/N0 - 1)*e^(-rt))
Это лишь некоторые примеры уравнений зависимости координаты от времени в различных областях науки. Каждое из них имеет свою специфику и применяется для описания конкретных физических явлений.
Практическое применение уравнений зависимости координаты от времени
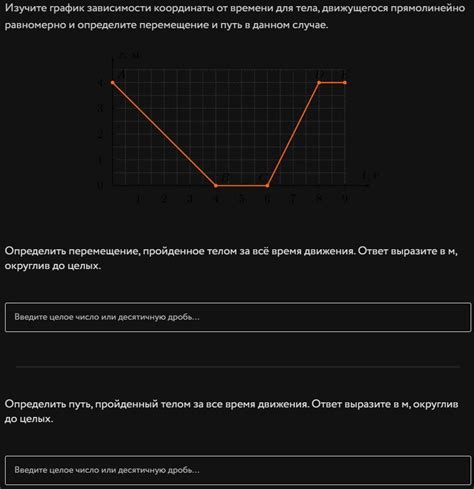
Уравнения зависимости координаты от времени находят широкое применение в различных областях науки и техники. Например, в физике они позволяют описывать движение тела, его траекторию и скорость. В астрономии использование этих уравнений позволяет определять положение небесных тел в разные моменты времени и прогнозировать их движение.
В механике уравнения зависимости координаты от времени используются для моделирования и прогнозирования движения различных механических систем, таких как автомобиль, самолет или роботы. Также они могут применяться для создания сложных машин с программно управляемыми движениями.
В инженерии и строительстве эти уравнения позволяют моделировать и анализировать поведение конструкций под действием различных нагрузок и воздействий времени. Это позволяет предсказать и предотвратить возможные повреждения и деформации конструкций, а также оптимизировать их конструктивные решения.
В биологии использование уравнений зависимости координаты от времени позволяет описывать движение и изменение формы живых организмов, таких как животные или растения. Это помогает исследователям лучше понять и объяснить различные физиологические процессы в организмах и развивать новые методы лечения и диагностики.
В области информационных технологий уравнения зависимости координаты от времени могут применяться для разработки алгоритмов позиционирования и навигации виртуальных и дополненной реальности, а также для создания интерактивных видеоигр и симуляторов.
Математическая формулировка уравнения зависимости координаты от времени
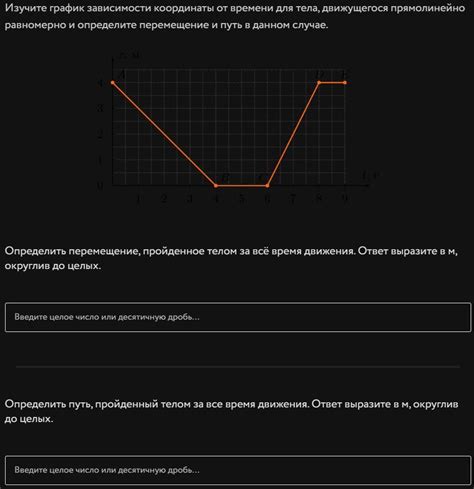
Обычно уравнение зависимости координаты от времени представляют в виде функции, где переменная времени обычно обозначается буквой t, а координата объекта обозначается буквой x. Такое уравнение можно записать следующим образом:
x = f(t)
Здесь x – это координата объекта в момент времени t, а f(t) – функция, которая описывает зависимость координаты от времени.
Уравнения зависимости координаты от времени могут иметь различные формы в зависимости от природы движения объекта. Например, для прямолинейного равномерного движения уравнение будет иметь вид:
x = v * t + x₀
Здесь v – скорость объекта, t – время, x₀ – начальная координата объекта.
Для других типов движений, таких как равноускоренное движение или движение по кривой траектории, уравнение будет выглядеть иначе, но все они имеют общую основу – описывают зависимость координаты от времени.
Методы решения уравнений зависимости координаты от времени
Уравнения зависимости координаты от времени в физике могут иметь различные формы и сложности. Для решения таких уравнений существует несколько методов, которые позволяют найти аналитическое или численное решение.
Один из основных методов решения уравнений зависимости координаты от времени – это метод разделения переменных. Суть метода заключается в предположении о виде решения, когда функция зависимости переменной разделяется на произведение функций от отдельных переменных. После подстановки такого предположения в уравнение и последующих преобразований получается система соотношений, решение которой позволяет определить значения функций. Данная техника широко применяется при решении линейных дифференциальных уравнений.
Еще одним методом решения уравнений зависимости координаты от времени является метод интегрирования. В этом методе уравнение интегрируется по времени для получения функции зависимости координаты от времени. Для этого необходимо знать начальные условия и интегрирующий множитель, который можно определить, исследуя свойства уравнения.
В случаях, когда уравнение не имеет аналитического решения или его получение затруднено, используются численные методы. Одним из таких методов является метод Эйлера. Он заключается в приближенном нахождении значения функции на следующем шаге по времени с использованием значения на текущем шаге и значения производной на этом шаге. Таким образом, можно последовательно находить значение функции на каждом шаге итерации.
Кроме того, существует множество других численных методов, таких как метод Рунге-Кутты, методы средней точки, методы Пикара и др. Все эти методы позволяют приближенно находить решение уравнений зависимости координаты от времени и широко применяются в различных областях науки и техники.



