Мир математики постоянно вводит нас в удивление и изумление своей бесконечной глубиной и непостижимыми законами. Одним из таких законов является возможность уравнения иметь бесконечно много корней. Это явление захватывает умы исследователей, так как с нашей интуитивной точки зрения мы ожидаем, что уравнение должно иметь конечное число корней.
Причины возникновения уравнений с бесконечным количеством корней могут быть различными. Одной из самых распространенных причин является наличие в уравнении переменной, которая принимает бесконечное количество значений. Например, если мы рассматриваем уравнение вида y = x^2, где y и x - переменные, то каждое значение переменной x будет соответствовать уникальному значению y. Поэтому, такое уравнение будет иметь бесконечное количество корней.
Последствия уравнений с бесконечным количеством корней можно наблюдать в различных областях науки и техники. Например, в физике уравнения с бесконечным числом корней могут использоваться для описания процессов, которые протекают в бесконечности. В экономике такие уравнения могут быть полезными при моделировании процессов, в которых возможны бесконечные вариации различных факторов.
Итак, уравнение имеющее бесконечное число корней может оказаться очень ценным и интересным объектом исследования в науке. Оно позволяет нам расширить наше понимание о мире и его законах, а также использовать его в различных практических областях нашей жизни.
Бесконечное количество корней в уравнении: причины и последствия

Одна из причин возникновения уравнения с бесконечным количеством корней – это простое уравнение, в котором все члены уравнения обращаются в ноль. Например, уравнение 0 = 0 не содержит ограничений для переменной и, следовательно, любое значение переменной является его корнем.
Другая причина – функциональные уравнения, которые позволяют получить бесконечное количество корней в зависимости от операций, примененных к переменным. Например, уравнение sin(x) = 0 имеет бесконечное множество корней, так как sin(x) равно 0 для всех значений переменной, кратных числу π.
Бесконечное количество корней в уравнении может иметь серьезные последствия. Например, при решении уравнения с бесконечным количеством корней нужно быть осторожным, чтобы не упустить какие-либо возможные оговорки или ограничения для переменной. Иногда это может привести к неправильным решениям или неучтению некоторых исключений.
Кроме того, уравнения с бесконечным количеством корней могут быть использованы для моделирования особенностей природных или математических процессов. Например, бесконечное количество корней может являться признаком периодического поведения или симметрии системы. Такие уравнения позволяют ученным и инженерам более точно описывать и прогнозировать различные явления и процессы.
Проблема с формулировкой уравнения

Для решения уравнения необходимо ясно сформулировать его, чтобы определить все его корни и достичь правильного результата. Однако, иногда встречаются случаи, когда уравнение поверхностно или неточно записано, что может привести к появлению бесконечного числа корней. В результате, решение становится неправильным или неоднозначным.
Часто это происходит, когда в уравнении присутствуют алгебраические операции, такие как деление на ноль или извлечение корня из отрицательного числа. Например, если уравнение содержит дробь с знаменателем равным нулю, то оно становится неопределенным и может иметь бесконечное количество корней.
Кроме того, формулировка уравнения может содержать некорректные математические операции, такие как деление на переменную или применение оператора к переменной другого типа данных. Это может привести к появлению неограниченного числа корней или к ошибке вообще.
При использовании сложных функциональных уравнений, особенно в физике и инженерии, важно тщательно просмотреть выражение и установить правильные диапазоны значений переменных. В противном случае, может произойти ситуация, когда уравнение окажется некорректно сформулированным и приведет к бесконечному числу корней или его отсутствию вовсе.
Для того, чтобы предотвратить проблемы с формулировкой уравнения, важно тщательно проверять все алгебраические операции, учитывать особенности математических функций и выполнять все переходы и преобразования с сохранением правил математики. Также, перед решением уравнения следует проверить его корректность и при необходимости перестроить его, чтобы избежать появления бесконечного числа корней.
Излишне сложные уравнения
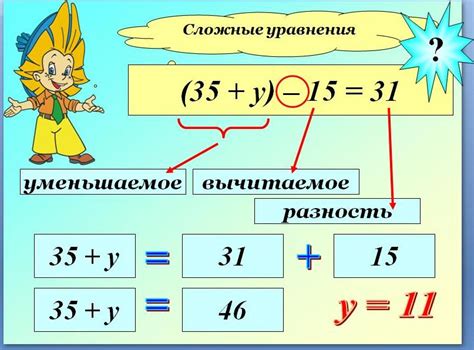
Существует класс уравнений, которые могут быть излишне сложными. Это происходит, когда в уравнении присутствуют элементы, которые делают его решение очень сложным или даже невозможным.
Одной из причин сложности уравнения может быть наличие высоких степеней в уравнении, например, кубического или квадратного корня. Такие элементы могут сделать решение уравнения крайне трудоемким и времязатратным.
Еще одной причиной сложности уравнения может быть наличие дробей. Когда в уравнении встречаются дробные числа или переменные, то его решение может потребовать дополнительных шагов и преобразований.
Иногда уравнения сложны из-за наличия неизвестных коэффициентов или параметров. В таком случае, для нахождения решения может потребоваться анализ различных комбинаций значений параметров.
Последствия излишне сложных уравнений могут быть различными. В некоторых случаях, нахождение точного или аналитического решения становится невозможным, и приходится прибегать к численным методам. Это может быть сложно или даже невозможно сделать вручную, поэтому требуется использование компьютерных программ или калькуляторов.
Кроме того, сложные уравнения могут создавать проблемы при анализе и интерпретации результатов. Если уравнение имеет множество решений или не имеет решений в определенном диапазоне значений, то это может привести к неправильному пониманию и принятию неверных решений.
В целом, излишне сложные уравнения представляют собой вызов для математиков и научных исследователей. Решение таких уравнений требует глубоких знаний и навыков, а также интуиции и творческого подхода к проблеме.
Использование несоответствующих методов решения
Одной из основных причин того, что уравнение имеет бесконечно много корней, может быть неправильный выбор метода решения. Некоторые методы решения уравнений не применимы к определенным типам уравнений или могут дать неверный результат.
Например, если уравнение является квадратным, то для его решения необходимо использовать формулу дискриминанта. Если же формула дискриминанта применяется к уравнению, не являющемуся квадратным, то результат может быть некорректным.
Также, некоторые уравнения могут содержать специальные функции, такие как тригонометрические или экспоненциальные функции. В таких случаях, использование методов решения, предназначенных для полиномиальных уравнений, может привести к неправильным корням или невозможности их нахождения.
Использование несоответствующих методов решения уравнений может привести к появлению бесконечного числа корней. Это может быть связано с тем, что неправильно выбранный метод не учитывает специфику уравнения и дает некорректные результаты.
Поэтому при решении уравнений необходимо тщательно выбирать метод и учитывать его соответствие типу и параметрам уравнения. Это поможет избежать ошибок и получить правильное решение уравнения.
Причины связанные с особенностями уравнений

Существуют несколько причин, по которым уравнение может иметь бесконечно много корней:
- Линейные зависимости в системе уравнений. Если в системе есть линейные зависимости между уравнениями, то это может привести к бесконечному количеству решений. Например, уравнение типа 2x + 3y = 7 с бесконечным количеством решений, так как все точки на прямой 2x + 3y = 7 являются его решениями.
- Симметричность уравнений. Некоторые уравнения могут быть симметричными относительно осей координат или других осей. Например, уравнение x^2 + y^2 = r^2 задает окружность с центром в начале координат. Окружность с центром в начале координат имеет бесконечно много точек, поэтому это уравнение имеет бесконечно много корней.
- Уравнения с неопределенными коэффициентами. В некоторых случаях, уравнения содержат неопределенные или переменные коэффициенты, которые могут принимать любые значения. Например, уравнение ax + by = c, где a, b и c - переменные коэффициенты, будет иметь бесконечно много корней, если a и b не равны нулю. Каждое значение a и b приведет к уникальному решению, поэтому решений будет бесконечное количество.
Уравнение с бесконечным количеством корней может иметь как практические, так и теоретические последствия. Например, если уравнение описывает физическую систему, то бесконечное количество решений может указывать на наличие бесконечного числа состояний системы. Это может быть полезно для анализа или моделирования поведения системы.
Последствия бесконечного количества корней
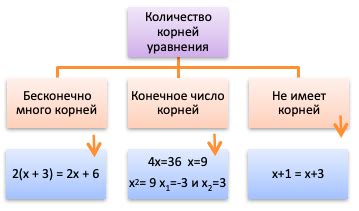
Когда уравнение имеет бесконечно много корней, это может иметь несколько последствий.
1. Один из возможных вариантов - это то, что уравнение является тождественным. В этом случае каждое значение переменной является корнем уравнения, и оно выполняется для любого числа.
2. Бесконечное количество корней может быть связано с функцией, которая повторяется или имеет периодическое поведение. При изучении таких функций, бесконечное количество корней может означать, что функция принимает одно и то же значение для нескольких разных значений переменной.
3. Бесконечное количество корней может также указывать на то, что уравнение имеет бесконечно много решений или семейств решений. Например, уравнение может быть параметрическим, где переменные связаны через параметры, и каждое значение параметра приводит к уникальному корню.
Для лучшего понимания и изучения бесконечного количества корней в уравнениях, часто используется таблица, где значения переменной и соответствующие им корни уравнения представлены в виде таблицы. Таблица позволяет увидеть закономерности и связи между переменными и корнями, что может помочь в дальнейшем анализе уравнения.
| Значение переменной | Корни уравнения |
|---|---|
| 1 | 1, 2, 3, 4, ... |
| 2 | 2, 4, 6, 8, ... |
| 3 | 3, 6, 9, 12, ... |
| ... | ... |
Как предотвратить возникновение бесконечного количества корней
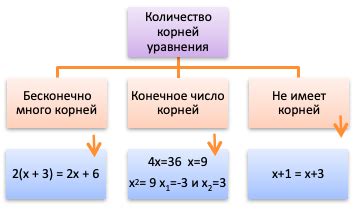
В некоторых случаях уравнение может иметь бесконечное количество корней. Это может привести к непредсказуемым результатам и затруднить решение задачи. Однако, существуют способы предотвратить возникновение бесконечного количества корней:
- Уточнение условий задачи: часто бесконечное количество корней возникает из-за неверных или неясных условий задачи. Пересмотрите задачу и убедитесь, что она содержит все необходимые ограничения и указания.
- Использование других методов решения: некоторые математические методы могут привести к бесконечному количеству корней, в то время как другие методы могут дать более точный и конкретный результат. Рассмотрите использование альтернативных методов решения уравнения.
- Уточнение значений переменных: иногда бесконечное количество корней возникает из-за неизвестных значений переменных. Постарайтесь определить и ограничить диапазон значений переменных, чтобы получить конкретный результат.
- Проведение дополнительных тестов: для проверки результатов решения уравнения проведите дополнительные тесты и сравните их с другими методами решения. Это поможет исключить возможность бесконечного количества корней и подтвердить правильность решения.
Следуя этим рекомендациям, вы сможете предотвратить возникновение бесконечного количества корней и получить более точный и конкретный результат при решении уравнений.



