Прямоугольный треугольник – одна из самых фундаментальных геометрических фигур. Он характеризуется наличием одного прямого угла (равного 90 градусам) и двух острых углов. Также в прямоугольном треугольнике имеются две стороны, смежные с прямым углом, – катеты, и одна сторона, лежащая напротив прямого угла, – гипотенуза.
Гипотенуза является самой длинной стороной прямоугольного треугольника. Она соединяет два катета и является противоположной прямому углу. Гипотенуза имеет решающее значение для геометрических и тригонометрических расчетов внутри прямоугольного треугольника.
Особенность гипотенузы заключается в том, что она всегда является наибольшей из трех сторон прямоугольного треугольника. Это свойство позволяет использовать гипотенузу как базу для вычисления длины катетов и углов треугольника.
Угол гипотенузы в треугольнике

Угол гипотенузы обычно обозначается как α или β в зависимости от того, какой катет он образует с гипотенузой. Для вычисления этого угла можно использовать тригонометрические функции, такие как синус, косинус или тангенс, а также известные значения других углов или длин сторон треугольника.
Знание угла гипотенузы может быть полезно при решении задач связанных с прямоугольными треугольниками. Например, по известным значениям двух углов и одного катета можно найти значение гипотенузы или другого катета с помощью тригонометрии. Кроме того, угол гипотенузы может быть использован в качестве измерения для определения формы и ориентации объектов, связанных с прямоугольными треугольниками, например, на плоских чертежах, планах или картографических материалах.
Таким образом, понимание и вычисление угла гипотенузы в треугольнике является важным элементом геометрии и тригонометрии, а также может быть применено практически в различных областях, где треугольники играют важную роль.
Значение угла гипотенузы
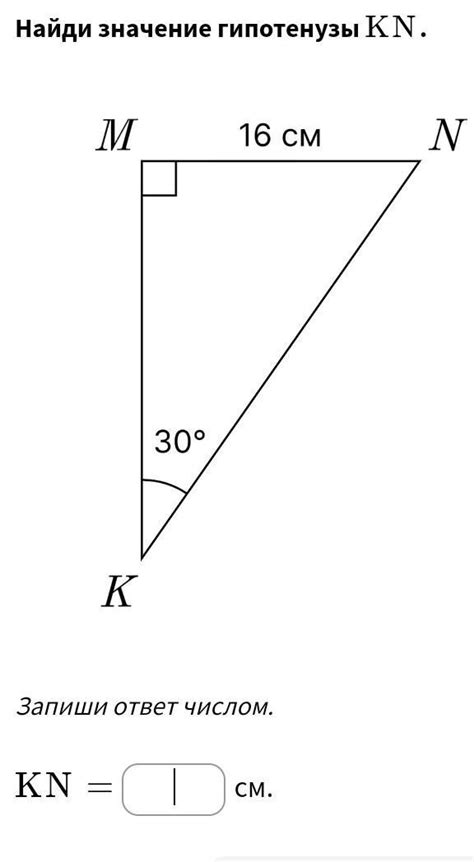
В прямоугольном треугольнике угол, лежащий напротив гипотенузы, называется прямым углом. Значение этого угла всегда равно 90 градусов.
Гипотенуза является наибольшей стороной в прямоугольном треугольнике и соединяет два острых угла. Ее значение зависит от длины катетов и может быть вычислено с помощью теоремы Пифагора.
Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов катетов:
| Теорема Пифагора: | c2 = a2 + b2 |
В этой формуле с - длина гипотенузы, a и b - длины катетов.
Зная значения катетов, можно легко вычислить значение гипотенузы по формуле теоремы Пифагора.
Значение угла гипотенузы в прямоугольном треугольнике всегда равно 90 градусам, что является важным свойством данной фигуры.
Гипотенуза в прямоугольном треугольнике
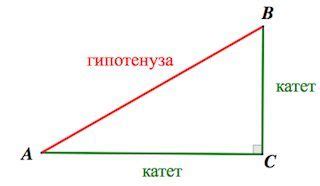
Гипотенуза в прямоугольном треугольнике связана с другими сторонами этого треугольника посредством теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов:
c2 = a2 + b2
Где c - длина гипотенузы, а a и b - длины катетов.
Эта формула позволяет найти длину гипотенузы, зная длины катетов, или наоборот - найти длину одного катета, если известны длина гипотенузы и другого катета.
Таким образом, гипотенуза является ключевым элементом прямоугольного треугольника и позволяет связать длины его сторон.



