Угол - это понятие, широко применяемое в геометрии и физике.
Угол представляет собой часть плоскости, ограниченную двумя лучами, исходящими из одной точки, называемой вершиной угла. Угол обладает несколькими характеристиками, включая величину и направление. Величина угла измеряется в градусах, радианах или других единицах измерения.
Угол состоит из нескольких составляющих. Во-первых, это вершина угла - точка, из которой выходят лучи. Вершина угла является общей точкой для обоих лучей. Во-вторых, угол имеет два луча, которые ограничивают его и определяют его размер. Каждый луч состоит из бесконечного числа точек, простирающихся от вершины.
Уголы могут быть классифицированы на основе их размеров. Обычно, угол с величиной от 0 до 90 градусов считается остроугольным. Угол, равный 90 градусам, называется прямым углом. Угол с величиной более 90 градусов и менее 180 градусов считается тупоугольным. Если угол равен 180 градусам, он называется прямой линией. Наконец, если угол превышает 180 градусов и менее 360 градусов, он считается вогнутым или рефлексным углом.
Определение и свойства угла

Основные свойства угла:
- Величина: угол измеряется в градусах (°), минутах ('), и секундах (") или в радианах (rad).
- Взаимное положение: углы могут быть смежными, вертикальными, суплементарными или комплементарными.
- Сумма: сумма углов в треугольнике равна 180°, а сумма углов в четырехугольнике равна 360°.
- Классификация: углы могут быть прямыми (90°), острыми (меньше 90°) или тупыми (больше 90°).
- Измерение: углы измеряются с помощью инструмента, называемого транспортиром.
Понимание определения и свойств угла является важным для изучения геометрии и решения различных задач, связанных с углами и их взаимным положением.
Угол: понятие и его характеристики
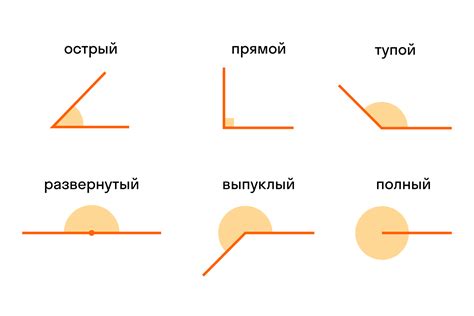
Углы могут быть измерены в градусах, радианах или градах. Один полный оборот составляет 360 градусов, 2π радианов или 400 градусов. Углы также могут быть измерены в отношении меньшего угла к большему, как доля полного оборота.
Углы могут быть классифицированы по своей величине: прямой угол равен 90 градусам (π/2 радианов), острый угол меньше 90 градусов (π/2 радианов), тупой угол больше 90 градусов (π/2 радианов) и полный угол равен 360 градусов (2π радианов).
Углы также могут быть классифицированы по положению и направлению: вертикальные углы образуются при пересечении двух прямых линий и имеют одинаковые углы, смежные углы образуются при пересечении двух прямых линий и имеют общую сторону, противоположные углы образуются при пересечении двух прямых линий и лежат по разные стороны от пересекающей их прямой.
Углы также могут быть классифицированы по форме: острые углы имеют меньшую величину, тупые углы имеют большую величину, прямые углы имеют величину 90 градусов (π/2 радианов) и полные углы имеют величину 360 градусов (2π радианов).
Размер угла: измерение и единицы измерения
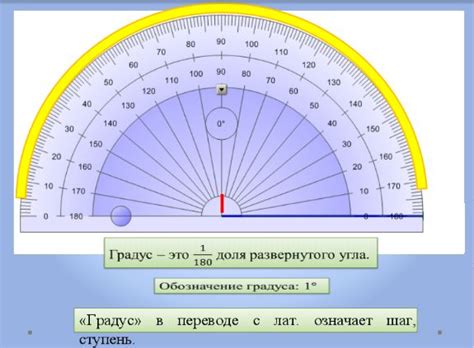
Градус - наиболее распространенная единица измерения углов. Одна полная окружность состоит из 360 градусов. Угол, равный 1/360 полной окружности, называется градусом.
Минута - это единица измерения угла, равная 1/60 градуса. Она обозначается символом ' и используется для измерения более точных углов.
Секунда - еще более маленькая единица измерения угла, равная 1/60 минуты или 1/3600 градуса. Она обозначается символом " и может быть использована для измерения самых точных углов.
Радиан - это другая единица измерения угла, которая основана на радиусе окружности. Одна полная окружность состоит из приблизительно 6,28318 радианов. Радиан используется чаще всего в математике и науке.
Град - это единица измерения, которая используется в некоторых странах. Она является производной от градуса. Один град равен 1/400 полной окружности или 0,9 градуса. Град используется в навигации и геодезии.
Независимо от выбранной единицы измерения, правильное измерение угла позволяет точно определить его размер и использовать в соответствующих вычислениях или построениях.
| Единица измерения | Символ | Величина |
|---|---|---|
| Градус | ° | 1/360 полной окружности |
| Минута | ' | 1/60 градуса |
| Секунда | " | 1/60 минуты или 1/3600 градуса |
| Радиан | рад | Приблизительно 6,28318 радианов в полной окружности |
| Град | град | 1/400 полной окружности или 0,9 градуса |
Виды углов: острые, прямые, тупые, смежные
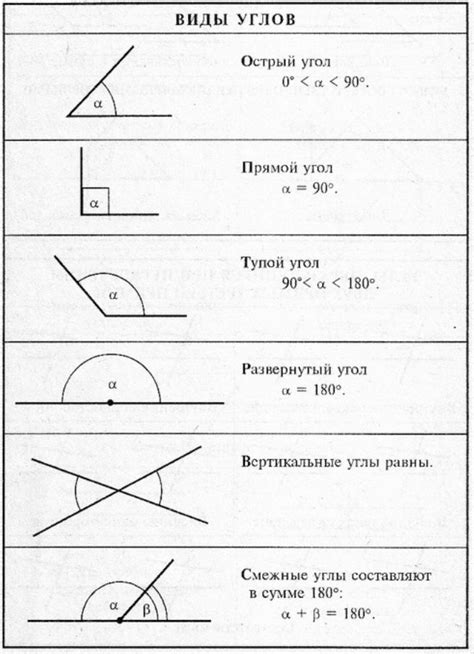
Острые углы имеют величину меньше 90 градусов. Такие углы выглядят, как часть прямой, которая сгибается, но не доходит до положения прямого угла.
Прямые углы имеют величину в 90 градусов. Такие углы выглядят, как часть прямой, которая делится пополам и образует две равные половины.
Тупые углы имеют величину больше 90 градусов. Такие углы выглядят, как часть прямой, которая сгибается в противоположную сторону от прямого угла.
Смежные углы - это углы, которые имеют общую сторону и общую вершину. При этом две другие стороны углов не пересекаются.
Смежные углы: определение и свойства

Определение смежных углов позволяет лучше понять их свойства и использовать их в геометрических задачах.
Свойства смежных углов:
- Сумма величин смежных углов равна 180 градусам. Например, если один угол измеряет 40 градусов, то второй угол будет измерять 140 градусов.
- Смежные углы могут быть как прилегающими, то есть находиться с одной стороны от общей стороны, так и вертикальными, то есть находиться по разные стороны общей стороны, но иметь общую вершину.
- Если смежные углы являются прилегающими и один из них прямой, то второй угол будет также прямым.
- Смежные углы могут быть как дополнительными, то есть сумма их величин равна 90 градусам, так и суплементарными, когда сумма их величин равна 180 градусам.
Изучение и понимание свойств смежных углов помогает решать задачи по геометрии, строить и анализировать фигуры, а также применять их в повседневной жизни.
Взаимные положения двух прямых и углов
Для понимания угла необходимо рассмотреть его взаимное положение с другими объектами, в частности, с прямыми.
Две прямые могут располагаться относительно друг друга по-разному:
1. Параллельные прямые: Если две прямые не пересекаются, то они называются параллельными. При этом они имеют одинаковое направление и одинаковое расстояние между собой на всем протяжении.
2. Пересекающиеся прямые: Если две прямые пересекаются в одной точке, то они называются пересекающимися.
3. Совпадающие прямые: Если две прямые полностью совпадают друг с другом, то они называются совпадающими. В этом случае все углы между ними равны 0°.
Угол также может находиться между прямыми:
1. Вертикальные углы: Вертикальные углы образуются при пересечении двух прямых. Они равны между собой и располагаются по разные стороны каждой из прямых.
2. Дополнительные углы: Два угла называются дополнительными, если сумма их мер равна 180° и они располагаются по разные стороны одной из прямых.
3. Смежные углы: Смежные углы образуются при пересечении двух прямых. Они имеют общую сторону и смежные стороны.
Понимание взаимных положений двух прямых и углов поможет более глубоко изучить свойства и законы, связанные с этими объектами в геометрии.
Сложный угол: определение и примеры
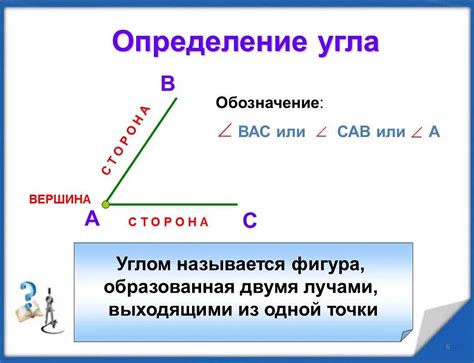
Примером сложного угла может служить угол, образованный двумя лучами - АВ и АС, имеющими общую начальную точку - точку А. Внутренняя часть этого угла состоит из двух отдельных частей - угла ВАС и угла САВ.
| Пример | Пояснение |
|---|---|
 | На рисунке показан сложный угол АВС, где АВ и АС - лучи, а А - общая вершина угла. Внутренняя часть угла состоит из двух частей - угла ВАС и угла САВ. |
 | Это другой пример сложного угла АХУ. В данном случае угол разделен на две непересекающиеся части - угол ХАУ и угол УАХ. |
Сложные углы могут иметь различные комбинации и формы, но всегда сохраняют основные характеристики - два луча, одну вершину и внутреннюю часть, состоящую из двух частей.
Расчёт углов: формулы и методы

Для решения геометрических задач, связанных с углами, необходимо знание основных формул и методов их вычисления. В данной статье мы рассмотрим некоторые из них.
1. Сумма углов в треугольнике:
- В прямоугольном треугольнике сумма углов равна 180 градусов.
- В произвольном треугольнике сумма углов также равна 180 градусов.
2. Вычисление углов на основе длин сторон:
- В прямоугольном треугольнике можно вычислить угол по теореме Пифагора и тригонометрическим функциям.
- В произвольном треугольнике углы можно вычислить с помощью теоремы косинусов и теоремы синусов.
3. Вычисление углов на основе координат:
- Если известны координаты вершин треугольника, углы можно вычислить с помощью тригонометрических функций и формулы для нахождения угла между векторами.
4. Вычисление углов на плоскости:
- При работе с углами на плоскости используются различные формулы и методы, такие как метод скалярного произведения векторов.
Знание данных формул и методов позволит вычислять углы в различных геометрических задачах, а также применять их при решении практических задач, связанных с углами.
Угол в геометрическом построении
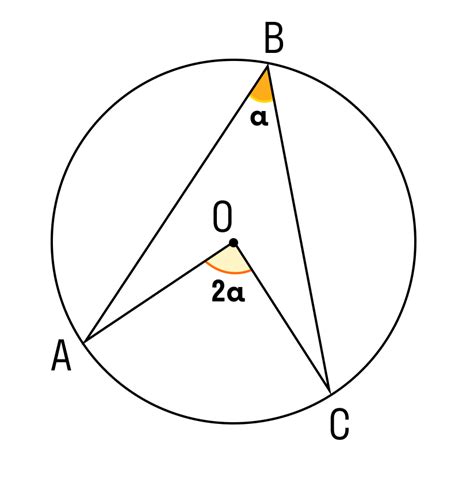
Уголы в геометрии могут быть различными по своей величине и форме. Углы бывают острыми, прямыми, тупыми или полными. Острый угол составляет менее 90 градусов, прямой угол равен 90 градусам, тупой угол больше 90 градусов и полный угол равен 180 градусам.
Углы широко используются в геометрии для измерения поворотов и направлений. Они играют важную роль в построении и измерении различных объектов, таких как треугольники, многоугольники и окружности.
Для обозначения углов используются специальные символы, которые ставятся над вершиной угла. Например, угол АВС может быть обозначен как ∠АВС.
Углы могут быть сравниваемыми и добавочными. Сравниваемые углы имеют одну сторону общую и направлены в разные стороны. Они могут быть равными, больше или меньше друг друга. Добавочные углы образуются двумя углами, сумма которых равна 90 градусам.
Понимание углов в геометрии является важным элементом для решения различных задач и построения сложных фигур. Хорошее усвоение основных концепций углов поможет сформировать базу для изучения более сложных разделов геометрии.
Практическое применение углов в жизни

Углы широко используются в различных сферах нашей жизни. Они помогают нам понять и измерить отношения, угловые повороты и направления.
В архитектуре углы используются для создания прочных и устойчивых конструкций. Архитекторы и строители используют углы при проектировании зданий и сооружений, чтобы гарантировать их устойчивость и безопасность.
В геометрии углы используются для измерения расстояния между двумя линиями или поверхностями. Они помогают определить форму и размеры различных геометрических фигур, таких как треугольники, круги и прямоугольники.
В навигации и картографии углы используются для определения направления и местоположения. Путешественники и моряки используют углы для определения своей текущей позиции и планирования маршрутов.
В фотографии и видеосъемке углы используются для создания эффекта глубины, перспективы и композиции. Фотографы и операторы используют разные углы съемки, чтобы создать интересные и привлекательные кадры.
В технике углы используются для проектирования и изготовления механизмов и инструментов. Инженеры используют углы при разработке деталей и машин, чтобы обеспечить их правильную работу и функциональность.
В спорте углы используются для измерения и оценки результатов. Углы применяются, например, для измерения пути и дистанции в легкой атлетике, а также для определения правильной техники выполнения различных движений.
- Архитектура - создание прочных и устойчивых конструкций.
- Геометрия - определение формы и размеров геометрических фигур.
- Навигация и картография - определение направления и местоположения.
- Фотография и видеосъемка - создание эффекта глубины и перспективы.
- Техника - проектирование и изготовление механизмов и инструментов.
- Спорт - измерение и оценка результатов.
Очевидно, что углы играют важную роль в разных областях нашей жизни. Они помогают нам понять и измерить различные аспекты окружающего мира и использовать эти знания в практическом применении.



