Тригонометрия – одна из важнейших разделов математики, изучающая связь между углами и сторонами треугольников. Она является фундаментальной для многих наук, включая физику, астрономию, инженерию и геометрию. Предмет изучения тригонометрии включает в себя углы, их измерение, тригонометрические функции и их свойства.
Одним из основных понятий в тригонометрии является угол. Угол – это фигура, образованная двумя лучами, исходящими из одной точки, называемой вершиной угла. Углы могут быть измерены в градусах, радианах или градах. В тригонометрии наиболее часто используются градусы и радианы.
Основные тригонометрические функции – синус, косинус и тангенс. Синус угла равен отношению противолежащей стороны к гипотенузе, косинус – отношению прилежащей стороны к гипотенузе, а тангенс – отношению противолежащей стороны к прилежащей.
Изучение тригонометрии помогает в решении различных задач, связанных с треугольниками, таких как нахождение длины стороны или угла, определение высоты или расстояния между объектами. Она также имеет множество приложений в реальной жизни, включая архитектуру, навигацию, астрологию и музыку.
Основы тригонометрии: принципы и приложения

Основой тригонометрии является тригонометрический круг, который представляет собой окружность с центром в начале координат. Углы в тригонометрии измеряются в радианах, а основные тригонометрические функции включают синус, косинус и тангенс.
Основным принципом тригонометрии является теорема Пифагора, которая устанавливает соотношение между сторонами прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов. Это соотношение позволяет находить значения тригонометрических функций для разных углов и сторон треугольников.
Тригонометрия находит свое применение во многих областях науки и техники. Например, в физике она используется для описания колебаний и волн, а в астрономии – для измерения расстояний между звездами и планетами. Тригонометрические функции также применяются в инженерии, строительстве, навигации и в других областях.
Важно отметить, что знание основ тригонометрии имеет практическую ценность и широко используется в повседневной жизни. Например, при решении задач связанных с построением и измерением, при ориентации на местности, при работе с геодезическими приборами и т.д.
Что такое тригонометрия и зачем ее изучать
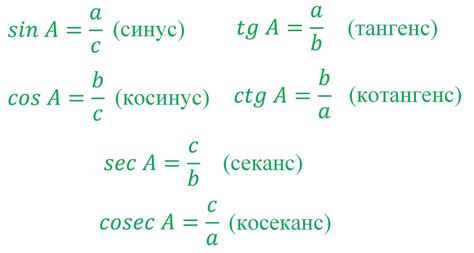
Основной предмет изучения тригонометрии - это тригонометрические функции, такие как синус, косинус и тангенс. Эти функции представляют отношения между сторонами и углами в треугольнике. Изучение тригонометрии позволяет нам решать разнообразные задачи, связанные с треугольниками и углами, в том числе нахождение неизвестных сторон и углов, вычисление площадей и объемов, а также моделирование и анализ колебаний и волн.
Также изучение тригонометрии развивает абстрактное мышление, логику и математическую интуицию. Она помогает нам понять и описать сложные явления и процессы в природе и технике, а также строить точные математические модели. Без тригонометрии мы бы не могли понять и предсказать многие физические и геометрические явления, которые окружают нас в повседневной жизни.
Таким образом, изучение тригонометрии является важным компонентом математического образования и имеет широкое применение в реальном мире. Оно помогает нам лучше понимать окружающий нас мир и решать разнообразные задачи в научных и технических областях.



