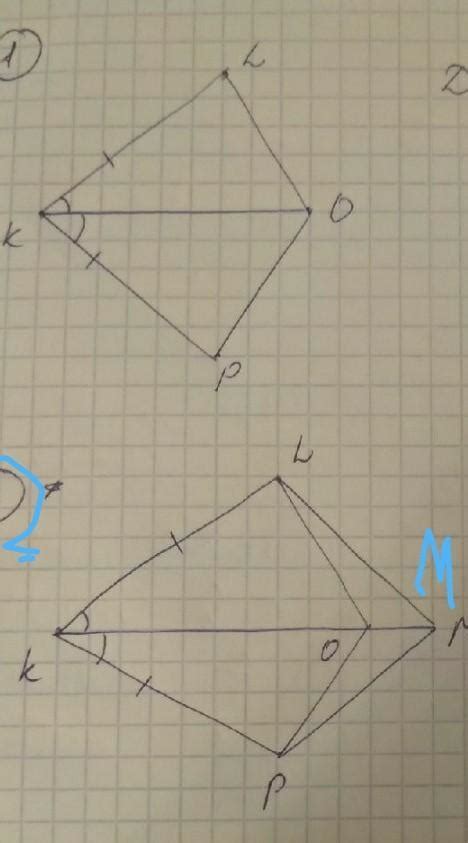
Треугольники lom и pom - это два треугольника, которые у нас есть. Нам нужно доказать их равенство, то есть показать, что они абсолютно идентичны друг другу.
Для доказательства равенства треугольников нам необходимо найти все соответствующие стороны и углы в обоих треугольниках и проверить их равенство. Это позволит нам убедиться, что треугольники lom и pom имеют одинаковую форму и размеры.
Сначала мы рассмотрим стороны треугольников lom и pom. Пусть стороны треугольника lom обозначаются как lo, om и ml, а стороны треугольника pom - как po, om и mp.
Если стороны треугольника lom равны соответственным сторонам треугольника pom, то мы можем сказать, что стороны этих треугольников одинаковы. Используя эту информацию, мы можем продолжить доказательство равенства треугольников.
Доказательство равенства треугольников
Для доказательства равенства треугольников необходимо выполнить следующие шаги:
Шаг 1: Проведем линии, соединяющие соответствующие вершины треугольников lom и pom.
Таким образом, если длины сторон и углы треугольников lom и pom оказались равными, то можно утверждать, что треугольники равны друг другу.
Замечание: для выполнения шагов 2 и 3 требуется использование инструментов измерения длины и углов.
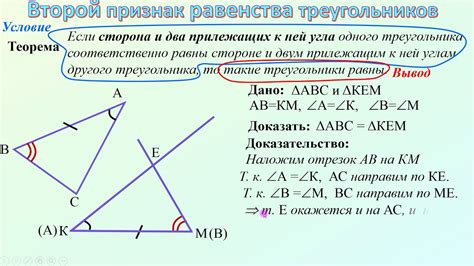
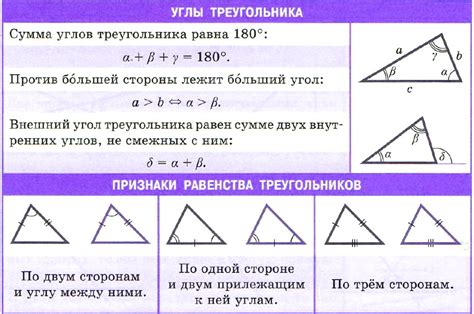
Теорема о равенстве треугольников

Теорема формулируется следующим образом: если у двух треугольников соответственно равны все три стороны или две стороны и вложенный между ними угол, или гипотенуза и катет прямоугольного треугольника, либо равны две гипотенузы прямоугольных треугольников и один катет каждого из них, или равны радиусы окружностей, вписанных в эти треугольники – то эти треугольники равны.
Основными методами доказательства равенства треугольников являются метод подобия, метод совмещения и метод конгруэнтности. Применяя эти методы и используя геометрические свойства, можно доказать равенство треугольников.
Теорема о равенстве треугольников имеет важное значение в геометрии, так как по ней можно вывести другие положения и свойства геометрических фигур. Эта теорема также используется при решении задач, связанных с построением треугольников и вычислением их параметров.
Треугольник lom
Стороны треугольника lom:
Сторона lo имеет длину √((x2 - x1)2 + (y2 - y1)2)
Сторона om имеет длину √((x3 - x2)2 + (y3 - y2)2)
Сторона ml имеет длину √((x1 - x3)2 + (y1 - y3)2)
Используя эти значения длин сторон, можно вычислить периметр треугольника lom, который равен сумме длин сторон.
Примерный вид треугольника lom:
l(x1, y1) _______o(x2, y2)
\
\
\
m(x3, y3)
Треугольник пом

Треугольник "pom" имеет три стороны и три угла, которые обозначаются как точка "p", точка "o" и точка "m".
Стороны треугольника "pom" обозначаются как "po", "op" и "om".
Углы треугольника "pom" обозначаются как "∠p", "∠o" и "∠m".
Треугольник "pom" может быть различной формы и размера, в зависимости от значений его сторон и углов.
Доказательство равенства треугольников "lom" и "pom" может основываться на равенстве их сторон и углов.
Условия равенства треугольников lom и pom
Для доказательства равенства треугольников lom и pom необходимо проверить выполнение следующих условий:
| Условие | Объяснение |
|---|---|
| LO = PO | Сторона LO треугольника lom должна быть равна стороне PO треугольника pom. |
| OM = OM | Сторона OM треугольника lom должна быть равна стороне OM треугольника pom. |
| ∠L = ∠P | Угол L треугольника lom должен быть равен углу P треугольника pom. |
Доказательство равенства lom и pom

Для доказательства равенства треугольников lom и pom необходимо установить, что их соответствующие стороны, углы и высоты равны.
- Стороны: Одна сторона треугольника lom равна стороне треугольника pom, так как они обе принадлежат отрезку om и являются его составляющими частями. Аналогично, остальные стороны треугольников lom и pom также равны.
- Углы: Углы треугольника lom и треугольника pom, смежные со стороной om, равны, так как они образованы пересечением прямых, проходящих через эту сторону. Таким образом, все углы треугольников lom и pom равны.
- Высоты: Высоты треугольника lom и треугольника pom, проведенные из вершины o, будут равны, так как они являются перпендикулярами к основанию om.
Таким образом, треугольники lom и pom равны по всем соответствующим элементам и, следовательно, равны в целом.



