Математика - это уникальная наука, которая рассматривает различные аспекты чисел, формул и операций. Она играет важную роль в нашей повседневной жизни, помогая нам развивать логическое мышление, аналитические навыки и принимать обоснованные решения. В школе ученики изучают различные области математики, включая геометрию, алгебру, арифметику и теорию.
Теория по математике 6 класса - это то, с чего начинается серьезное изучение математики в школе. В 6 классе ученики углубляются в арифметику и начинают изучать алгебру и геометрию. Это важный этап в учебном процессе, на котором ученики учатся решать различные математические задачи, анализировать их и применять полученные знания в повседневной жизни.
В теории по математике 6 класса ученики изучают такие темы, как действия с дробями, рациональные числа, алгебраические выражения, уравнения и неравенства, геометрические фигуры, расстояние и площадь, вероятность и многое другое. Они также учатся строить математические модели, решать задачи и объяснять свои решения. Изучение теории по математике в 6 классе помогает ученикам развивать свои математические навыки, а также готовит их к более сложным темам и концепциям, которые будут изучаться в старших классах.
Основные понятия и определения

| Понятие | Определение |
|---|---|
| Число | Абстрактное понятие, которое обозначает количество или позицию в некотором упорядоченном множестве. |
| Числовая прямая | Множество всех чисел, расположенных на прямой в соответствии с их величиной и упорядоченных. |
| Целое число | Число, которое представляет собой натуральное число, его противоположность или ноль. |
| Дробь | Выражение вида a/b, где a и b - целые числа, а b не равно нулю. |
| Процент | Стандарт для измерения доли или части от целого. |
| Сравнение чисел | Операция, которая позволяет сравнить числа и установить их отношение (больше, меньше или равно). |
Понимание этих основных понятий и определений поможет ученикам 6 класса разобраться с математическими задачами и концепциями, которые они встретят в курсе математики.
Объединение и пересечение множеств

В математике существуют две основные операции над множествами: объединение и пересечение. Они позволяют объединять и находить общие элементы двух или более множеств.
Объединение множеств - это операция, которая позволяет создать новое множество, состоящее из всех элементов, принадлежащих хотя бы одному из исходных множеств. Обозначается символом "∪". Например, объединение множеств A и B обозначается как A ∪ B и содержит все элементы из множества A и множества B.
| Множество A | Множество B | Объединение A ∪ B |
|---|---|---|
| {1, 2, 3} | {2, 3, 4} | {1, 2, 3, 4} |
| {a, b, c} | {c, d, e} | {a, b, c, d, e} |
Пе
Основные свойства чисел

В математике существуют различные типы чисел. Но независимо от конкретной системы чисел, они обладают несколькими основными свойствами, которые помогают в их изучении и применении:
- Свойство равенства: два числа равны между собой, если они имеют одинаковую величину или значение. Равные числа обозначаются символом "=". Например, 5 = 5.
- Свойство неравенства: два числа неравны между собой, если они имеют различную величину или значение. Неравенство обозначается символом "≠". Например, 3 ≠ 7.
- Свойство порядка: числа можно сравнивать по величине. Для этого используются знаки ">", " 3 означает, что число 5 больше числа 3.
- Свойство ассоциативности: для операции сложения (или умножения) не имеет значения, в каком порядке будут сложены (умножены) числа. Например, (2 + 3) + 4 = 2 + (3 + 4). Это свойство можно использовать для упрощения выражений.
- Свойство коммутативности: порядок, в котором складываются (или умножаются) числа, не влияет на результат. Например, 2 + 3 = 3 + 2. Это свойство можно использовать для перестановки слагаемых или множителей местами.
- Свойство распределительности: умножение числа на сумму двух чисел равно сумме произведений этого числа на каждое из слагаемых. Например, 2 * (3 + 4) = (2 * 3) + (2 * 4).
Знание основных свойств чисел позволяет более глубоко понять и использовать математические операции и отношения между числами.
Простые и составные числа
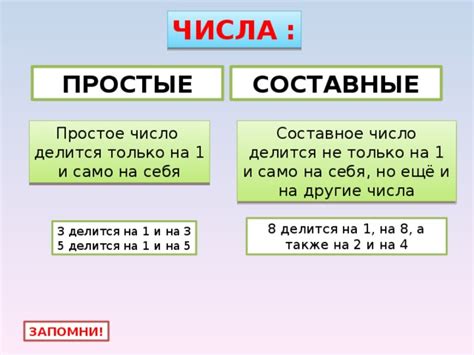
В математике числа делятся на две основные категории: простые и составные числа.
Простые числа - это числа, которые имеют только два делителя: единицу и само число. Примеры простых чисел: 2, 3, 5, 7, 11 и т.д. Простые числа нельзя разложить на произведение других чисел кроме единицы и самого числа.
Например, число 7 является простым, так как его единственные делители - 1 и 7, а число 8 является составным, так как его делители - 1, 2, 4 и 8.
Составные числа - это числа, которые имеют более двух делителей. Они могут быть разложены на произведение простых чисел. Например, число 12 является составным, так как его делители - 1, 2, 3, 4, 6 и 12, и его можно разложить на произведение простых чисел: 2 * 2 * 3.
Понимание различий между простыми и составными числами является важным элементом в изучении математики, и оно позволяет нам лучше понять свойства и возможности чисел.
Делители числа и кратность

Для определения делителей числа можно использовать метод простого деления числа на все возможные числа до его половины. Если число делится без остатка, то это число является делителем.
Кратность числа - это количество раз, на которое данное число делится на другое число без остатка. Например, число 6 кратно числу 3, так как 6 делится на 3 без остатка один раз.
Для определения кратности числа можно поделить это число на другое число и проверить, делится ли оно без остатка.
Важно запомнить:
- Число всегда является делителем для самого себя.
- Натуральные числа являются делителями для всех целых чисел.
- Единица является делителем для любого числа.
Пример:
Пусть дано число 16. Его делители: 1, 2, 4, 8, 16. Кратность числа 16 кратно числу 4, так как 16 делится на 4 без остатка четыре раза.
Нахождение НОК и НОД

Для нахождения наименьшего общего кратного (НОК) и наибольшего общего делителя (НОД) двух чисел, необходимо использовать определенные алгоритмы и методы.
НОК (наименьшее общее кратное) двух чисел - это наименьшее положительное число, которое делится без остатка и на первое число, и на второе. НОК часто используется в задачах, связанных с общими числителями и знаменателями.
НОД (наибольший общий делитель) двух чисел - это наибольшее положительное число, которое одновременно является делителем обоих чисел. НОД также широко используется в математических вычислениях и приведении дробей к общему знаменателю.
Существует несколько методов для нахождения НОК и НОД:
- Метод простого деления (перебор делителей).
- Метод простых чисел и степеней.
- Метод алгоритма Евклида.
Метод простого деления заключается в переборе всех чисел от 2 до меньшего из двух чисел и нахождении их общих делителей. Из полученных результатов выбирается наибольший общий делитель, который и будет НОДом.
Метод простых чисел и степеней основан на использовании разложения чисел на простые множители и их степени. НОК находится путем умножения наибольших степеней каждого простого множителя.
Метод алгоритма Евклида использует деление чисел с остатком. Он заключается в последовательном делении второго числа на первое до получения нулевого остатка. НОД равен последнему положительному остатку.
Рациональные и иррациональные числа
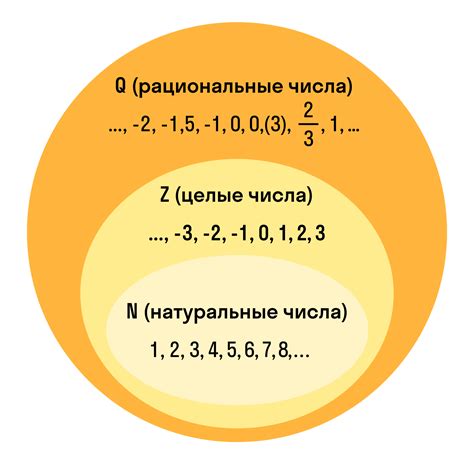
Иррациональные числа – это числа, которые не могут быть представлены в виде дроби. Их десятичная запись бесконечна и непериодична. Например, число π (пи) = 3.1415926535... и число √2 (квадратный корень из 2) не могут быть точно представлены в виде дроби и являются иррациональными.
Для удобства работы с рациональными и иррациональными числами в математике используется десятичная система счисления. Рациональные числа имеют конечное или периодическое представление в десятичной форме, в то время как иррациональные числа имеют бесконечное и непериодическое десятичное представление.
Таким образом, рациональные и иррациональные числа – это два класса чисел, которые дополняют друг друга и вместе образуют множество всех действительных чисел.
| Примеры рациональных чисел | Примеры иррациональных чисел |
|---|---|
| 2 | √2 |
| -5/3 | π (пи) |
| 0.75 | е (экспонента) |
Правила умножения и деления
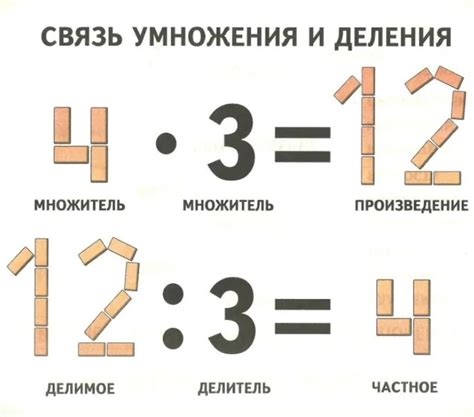
Правила умножения:
- Умножение числа на 1 не изменяет самого числа. Это называется умножение на единицу.
- Умножение числа на 0 всегда дает результат 0.
- Умножение числа на -1 меняет знак числа на противоположный. Это называется умножение на минус единицу.
- Если умножить два положительных числа или два отрицательных числа, то результат будет положительным.
- Если один из множителей отрицателен, а другой положителен, то результат будет отрицательным.
- Порядок умножения не влияет на результат, то есть, a * b = b * a.
- Чтобы умножить число на 10, нужно приписать к нему один ноль справа.
Правила деления:
- Делить на 1 не изменяет самого числа. Это называется деление на единицу.
- Делить на 0 невозможно, так как результатом будет бесконечность или неопределенность.
- Деление двух одинаковых чисел дает результат 1.
- Если делитель положительный, а делимое отрицательное, то результат будет отрицательным.
- Если делитель отрицательный, а делимое положительное, то результат будет отрицательным.
- Деление двух положительных чисел дает положительный результат, а деление двух отрицательных чисел также дает положительный результат.
- Чтобы разделить число на 10, нужно удалить один знак после запятой и сдвинуть запятую на один разряд влево.
Правила умножения и деления помогают упрощать и решать различные математические задачи. Знание этих правил развивает логическое мышление и умение работать с числами.
Геометрические фигуры и их свойства
- Отрезок - участок прямой между двумя точками. Отрезок имеет начальную и конечную точки, длину, которую можно измерить с помощью линейки.
- Угол - область в пространстве, образованная двумя лучами, имеющими общее начало. Угол измеряется в градусах и может быть острый, прямой, тупой или полный.
- Треугольник - фигура, образованная тремя отрезками, называемыми сторонами. Треугольник может быть различных типов: остроугольный, прямоугольный (один из углов равен 90 градусов), тупоугольный или равносторонний (все стороны равны).
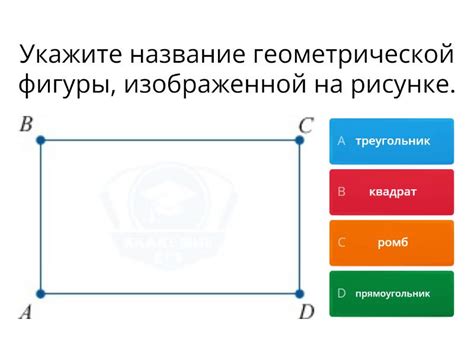
- Прямоугольник - четырехугольник, у которого все углы прямые.
- Квадрат - прямоугольник, у которого все стороны равны.
- Круг - фигура, образованная всеми точками, находящимися на одинаковом расстоянии от центра. Круг имеет радиус (расстояние от центра фигуры до любой точки на его границе) и диаметр (удвоенный радиус).
Изучение геометрических фигур и их свойств позволяет ученикам развивать воображение, логическое мышление и умение применять математические знания на практике. Кроме того, геометрия помогает понимать структуру и форму предметов в окружающем мире.



