Тарталья – это одно из самых ярких и значимых имен в истории математики. Итальянский ученый и математик, он оставил свой след в различных областях науки. Имя Тарталья известно многим школьникам, ведь его достижения и изобретения имеют особое значение для изучения математики в младших классах.
Тарталья был одним из первых математиков, которые активно изучали алгебру, а его открытия и методы используются до сих пор. Его имя стало нарицательным и используется в разных контекстах, связанных с изучением математики.
Одним из наиболее известных достижений Тартальи стало создание метода решения кубического уравнения. Этот метод, который называется "методом Тартальи", позволяет найти корни кубического уравнения в виде десятичных дробей. Благодаря ему, математики по всему миру смогли решать сложные задачи и уравнения, связанные с кубическими функциями.
Жизнь итальянского математика Тарталья

Никола Фонтана, более известный как Тарталья, был итальянским математиком, жившим в XVI веке. Родился он в 1499 году в городе Брешиа в Италии. О ранних годах его жизни не сильно много известно, но стало ясно, что Тарталья занимался математикой с удовольствием с раннего детства.
Однако жизнь Тартальи не всегда была так проста. В юности он попал втянулся в спор с другим математиком, по имени Фиоре. Этот спор стал причиной для великого достижения Тартальи - открытия формул для решения кубического уравнения.
Тарталья применил свои математические навыки и разработал метод для решения сложных уравнений. Он описал его в своей книге "General Trattato di Numeri et Misura", которая была опубликована в 1556 году. Он решил уравнение третьей степени, о котором тогда знало немного людей. Результаты его исследований были революционными и внесли вклад в развитие математики.
Тарталья также пользовался большой популярностью среди учеников и коллег. Он был уважаемым учителем и проводил лекции по математике в разных городах Италии. Многие из его учеников стали известными математиками и сделали свой вклад в развитие этой науки.
К сожалению, Тарталья не дожил до старости. Он умер в 1557 году в возрасте 57 лет. Однако его наследие продолжает жить до сих пор. Работы Тартальи стали основой для дальнейших разработок в области алгебры и теории уравнений. Его вклад в историю математики невозможно переоценить.
Вклад Тарталья в математику

Одним из наиболее известных достижений Тартальи является открытие формулы для решения кубического уравнения. В 1535 году он опубликовал свое открытие в своей книге "General Trattato di Numeri et Misure", которая стала первым крупным трудом, посвященным решению уравнений третьей степени. Формула Тартальи позволила решать кубические уравнения, которые ранее считались неразрешимыми.
Кроме того, Тарталья сделал значительный вклад в развитие комбинаторики. Он разработал новый метод комбинаторного анализа, который позволил решать сложные задачи, связанные с подсчетом возможных комбинаций и перестановок объектов. Его работы в этой области стали основой для последующих исследований и разработок в комбинаторике.
Тарталья также считается одним из основателей теории вероятностей. В своей книге "Trattato di Numeri et Misure" он ввел понятие вероятности и разработал некоторые базовые правила, на которых основывается современная теория вероятностей.
В целом, вклад Никколо Тартальи в математику был огромным. Его открытия и идеи продолжают влиять на различные области математики, а его работы считаются классическими источниками знаний.
Тарталья и решение кубического уравнения

Николо Фонтана, известный под прозвищем Тарталья, был итальянским математиком XVI века. Он сделал значительный вклад в развитие математики и стал основателем отрасли, известной как "алгебраическое решение уравнений". Одним из его наиболее известных достижений было решение кубического уравнения.
Тарталья разработал метод решения кубического уравнения в 1530 году. Этот метод позволял находить корни уравнения, которые ранее считались неразрешимыми. Благодаря своему открытию, Тарталья стал первым математиком, который смог найти аналитическое решение для этого типа уравнений.
Решение кубического уравнения с помощью метода Тартальи основано на использовании формул для суммы двух кубов. Он разбил исходное уравнение на два подуравнения и преобразовал их при помощи этих формул. Таким образом, он получил новое уравнение, которое можно легко решить, используя более простые методы.
За свои достижения в области математики Тарталья получил широкое признание и признание от ученых своего времени. Его метод решения кубических уравнений стал мощным инструментом для дальнейшего развития математики и был использован многими учеными после него.
Известные теоремы Тартальи
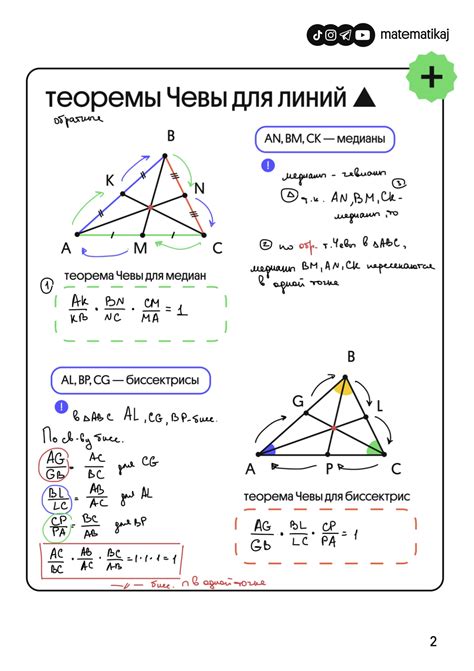
1. Теорема о вычислении кубического корня
Тарталья впервые разработал методы вычисления кубических корней. Он предложил формулу для определения действительного кубического корня из числа и показал, что этот метод решает уравнение вида x^3 = a.
2. Теорема о решении квадратных уравнений
Одной из самых известных теорем Тартальи является его метод решения квадратного уравнения вида ax^2 + bx + c = 0. Он предложил формулы для нахождения корней квадратного уравнения и показал, что его метод применим для всех квадратных уравнений.
3. Формула для расчета объема тетраэдра
Тарталья разработал формулу для расчета объема тетраэдра – одного из простейших многогранников. С помощью этой формулы можно определить объем любого тетраэдра, если известны длины его сторон и площадь одной из его граней.
4. Теорема о сумме углов в треугольнике
Тарталья доказал теорему, которая гласит, что сумма углов в любом треугольнике равна 180 градусам. Эта теорема является одной из основ треугольной геометрии и имеет множество применений в математике и физике.
5. Теорема о выпуклом многоугольнике
Тарталья изучал свойства выпуклых многоугольников и сформулировал теорему, которая гласит: "Сумма внутренних углов любого выпуклого многоугольника равна сумме (n-2) прямых углов". Эта теорема позволяет вычислять сумму внутренних углов многоугольника, зная только количество его сторон.
Учебная деятельность Тартальи

Геронимо Кардано, итальянский математик XVI века, был одним из учеников и коллег Никола Тартальи. Вместе с ним Тарталья изучал основы алгебры и геометрии.
Тарталья стал знаменитым благодаря своему открытию решения кубического уравнения. В 1548 году он использовал свои знания алгебры, чтобы разработать методику решения такого типа уравнений и даже опубликовал свои наработки. Однако, он еще долгое время сохранял в тайне полный метод, поэтому его открытие осталось неизвестным другим математикам. Но когда Тарталья узнал, что его метод был разглашен другим исследователем, он решил опубликовать свои достижения.
Несмотря на свои математические достижения, Тарталья не стал профессором, и вместо этого занимался преподавательской деятельностью. Он работал с учениками, обучая им алгебре и геометрии. Благодаря своим учебникам и лекциям, Тарталья стал известным ученым и преподавателем.
Тарталья также ввел новые математические символы и обозначения, которые некоторые из них применяются и по сей день. Он также был первым математиком, вводившим ипсилон и дельта для обозначения бесконечных и бесконечно малых чисел, что послужило основой развития математического анализа.
Международное признание Тартальи

Итальянский математик Никколо Тарталья был известен не только в Италии, но и за ее пределами. Его знания и достижения в области математики принесли ему международное признание и уважение со стороны ученых и математиков со всего мира.
Тарталья стал известным благодаря своей работе над применением математики в практических областях, особенно в сфере артиллерии. Он разработал новые методы решения канонических уравнений третьей степени, которые были особенно полезны в решении проблем, связанных с прицеливанием орудий.
Заслуги Тартальи в области математики были признаны многими учеными его времени. Он был удостоен высоких почестей и приглашен преподавать ведущими университетами и академиями Европы. Его работы и приложения математики использовались в различных научных и инженерных областях, принося пользу и развитие социуму в целом.
Тарталья оставил неизгладимый след в истории математики и его вклад в развитие этой науки был признан и восхищен не только в ее родной Италии, но и во всем мире. Его методы и подходы, вместе с его научными достижениями, стали основой для многих последующих математических теорий и разработок.
Научные достижения Тартальи

Никколо Фонтано, также известный как Тарталья, был известным итальянским математиком, жившим в 16 веке. Он внес значительный вклад в предмет, включая развитие алгебры и решение кубических уравнений.
Одним из наиболее известных достижений Тартальи является его решение кубического уравнения с положительным дискриминантом. До того момента этот тип уравнения не имел известного общего решения, и Тарталья смог найти эффективный метод его решения.
Он также разработал систему символов для представления алгебраических уравнений, что существенно упростило работу с ними и стало основой для дальнейшего развития алгебраической символики.
Достижения Тартальи в области математики имели значительное влияние на развитие этой науки и считаются важными шагами вперед в математической истории.
Наследие и влияние Тартальи в настоящее время
Итальянский математик Николо Тарталья, живший в XVI веке, оставил свой след в истории математики и науки в целом. Его неоспоримый вклад и научные достижения в области алгебры и геометрии продолжают влиять на современное математическое мышление.
Одним из главных наследий Тартальи было открытие и публикация метода решения кубического уравнения, то есть уравнения вида ax^3 + bx^2 + cx + d = 0. Этот метод, известный как "метод Тартальи-Кардано", имел огромное значение и стал отправной точкой для дальнейшего развития алгебры и теории уравнений.
Еще одно важное достижение Тартальи было связано с поиском решений задачи нахождения корней некоторых геометрических фигур. Он разработал метод, который позволял находить объем и площадь некоторых фигур, основываясь на собственных математических расчетах и идеях.
Сегодня идеи и методы Тартальи используются и развиваются в современной математике. Его работы по теории уравнений и геометрии являются основой для дальнейших исследований и разработок в этих областях. Многие математики признают его вклад в развитие математики и великим достижением для науки.



