В геометрии многоугольником называется фигура, образованная отрезками, называемыми сторонами, которые соединяются в вершинах. Сумма внешних углов многоугольника - это одно из интересных свойств этой геометрической фигуры. В данной статье мы рассмотрим формулу для вычисления суммы внешних углов многоугольника и приведем примеры для более наглядного представления.
Для начала, давайте определимся с понятием внешнего угла. Внешний угол многоугольника - это угол между продолжением одной из его сторон и продолжением соседней стороны. Важно отметить, что сумма внешних углов многоугольника всегда равна 360 градусов. Это правило справедливо независимо от количества сторон многоугольника и вида фигуры.
Теперь давайте рассмотрим формулу, которая позволяет вычислить сумму внешних углов многоугольника. Если у нас есть многоугольник с n сторонами, то сумма его внешних углов будет равна 360 градусов. Формула для вычисления внешнего угла многоугольника выглядит следующим образом: каждый внешний угол равен 360 / n градусов.
Например, для треугольника, у которого n=3, сумма внешних углов будет равна 360 / 3 = 120 градусов. Для четырехугольника, у которого n=4, сумма внешних углов будет равна 360 / 4 = 90 градусов. При этом внешний угол треугольника равен 120 градусам, внешний угол четырехугольника равен 90 градусам и так далее.
Значение суммы внешних углов многоугольника
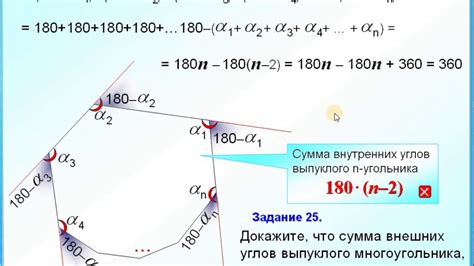
Сумма внешних углов многоугольника равна 360 градусов. Это означает, что если мы пройдем вокруг многоугольника и измерим все его внешние углы, их сумма будет всегда равна 360 градусов.
Это принцип выполняется для любого многоугольника, независимо от его формы или количества углов. Например, для треугольника сумма его внешних углов также будет равна 360 градусов. В случае треугольника, каждый его угол будет являться внешним, так как он не имеет других углов.
Формула для вычисления суммы внешних углов многоугольника можно записать следующим образом: S = 360°, где S - сумма внешних углов.
Знание значения суммы внешних углов многоугольника может быть полезно при решении задач геометрии или при измерении углов при работе с многоугольными фигурами.
Геометрическое определение суммы внешних углов

Для нахождения суммы внешних углов многоугольника можно использовать следующий подход:
- Выберите одну из вершин многоугольника.
- Проведите прямую через эту вершину параллельно одной из сторон многоугольника.
- Найдите внешний угол, образованный этой прямой и соседней стороной многоугольника.
- Повторите шаги 2 и 3 для каждой вершины многоугольника.
- Сложите все найденные внешние углы многоугольника, чтобы получить сумму внешних углов.
Например, для треугольника (трехугольника) сумма внешних углов будет равна 360 градусов, так как каждый внешний угол треугольника равен 120 градусам (поскольку сумма углов треугольника равна 180 градусам).
Геометрическое определение суммы внешних углов позволяет более наглядно представить связь между внешними и внутренними углами многоугольника, а также использовать это знание при решении различных задач из геометрии.
Формула для расчета суммы внешних углов многоугольника
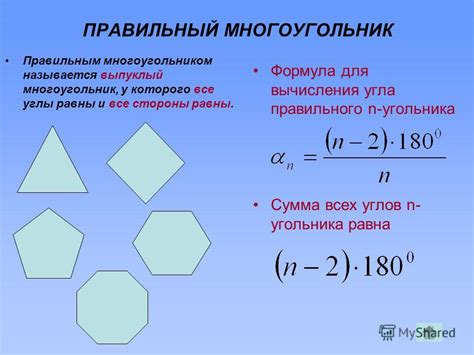
Сумма внешних углов многоугольника всегда равна 360 градусов. Это свойство имеет место для любого многоугольника, независимо от количества его сторон и при мгновенном суммировании всех его внешних углов.
Для нахождения суммы внешних углов многоугольника можно использовать следующую формулу:
- Подсчитайте количество сторон многоугольника. Обозначим это число как "n".
- Используйте формулу: сумма внешних углов = 360°.
- Разделите 360 на количество сторон многоугольника: сумма внешних углов = 360° / n.
Например, если у многоугольника 6 сторон, то сумма его внешних углов будет равна:
сумма внешних углов = 360° / 6 = 60°.
Таким образом, сумма внешних углов многоугольника с 6 сторонами равна 60 градусам.
Эта формула удобна для быстрого нахождения суммы внешних углов многоугольника и может быть использована в решении различных геометрических задач.
Важность понимания суммы внешних углов многоугольника
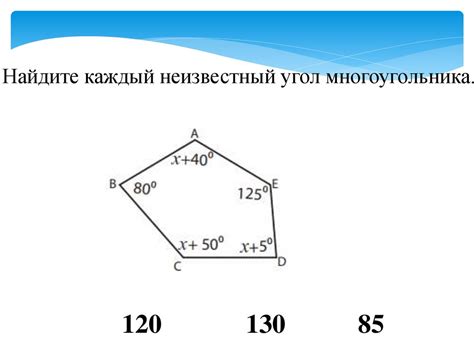
Знание формулы и причин, определяющих сумму внешних углов многоугольника, помогает при вычислениях и определении угловой меры точек, в которых прямые пересекаются с многоугольником. Использование правил и связей между внешними углами и другими элементами многоугольника позволяет проверять правильность построения и определения его формы.
Более того, понимание суммы внешних углов многоугольника позволяет решать задачи на применение геометрических прогрессий и найти недостающие углы и стороны. Это могут быть как практические задачи по землеустройству, архитектуре и дизайну, так и задачи из математики, которые помогают развивать логическое мышление и пространственную интуицию.
Наконец, понимание суммы внешних углов многоугольника имеет практическое применение в рамках различных профессий и деятельностей, связанных с геометрией. Это может быть полезно математикам, инженерам, архитекторам, графическим дизайнерам и другим специалистам, для которых знание геометрии является неотъемлемой частью их работы.
Таким образом, понимание суммы внешних углов многоугольника является важным и полезным знанием, которое может быть применено в различных сферах и повседневной жизни. Оно помогает развивать абстрактное и пространственное мышление, а также способствует развитию навыков логического мышления и решения задач.
Примеры расчета суммы внешних углов многоугольника
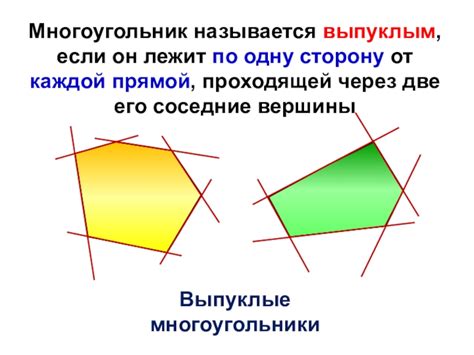
Сумма внешних углов многоугольника всегда равна 360 градусов. Это можно доказать с помощью нескольких простых примеров расчета.
Пример 1: Рассмотрим треугольник. В треугольнике всего три внешних угла. По формуле сумма внешних углов равна 360 градусов. В треугольнике каждый внешний угол равен 120 градусов, так как треугольник состоит из трех равных частей (120 + 120 + 120 = 360).
Пример 2: Рассмотрим четырехугольник. В четырехугольнике всего четыре внешних угла. Так как сумма внешних углов равна 360 градусов, в четырехугольнике каждый внешний угол должен быть равен 90 градусов (90 + 90 + 90 + 90 = 360).
Пример 3: Рассмотрим пятиугольник. В пятиугольнике всего пять внешних углов. По формуле сумма внешних углов равна 360 градусов. Зная, что сумма углов в пятиугольнике равна 540 градусов, можно вычислить каждый внешний угол, разделив 360 на 5. Таким образом, каждый внешний угол пятиугольника равен 72 градусам (72 + 72 + 72 + 72 + 72 = 360).
Таким образом, сумма внешних углов многоугольника всегда равна 360 градусов, независимо от количества сторон многоугольника.
Пример 1: треугольник
Рассмотрим пример треугольника для лучшего понимания формулы суммы внешних углов многоугольника. Треугольник имеет три стороны и три вершины.
У треугольника всегда имеются 3 внешних угла, которые образуются при продолжении каждой из его сторон. Сумма внешних углов треугольника всегда равна 360 градусов.
Например, рассмотрим треугольник ABC.
Угол A представляет собой внешний угол треугольника и равен сумме углов B и C внутри треугольника. Поэтому, если угол B равен 60 градусов, а угол C равен 80 градусов, то угол A будет равен 140 градусов.
Аналогично, углы B и C также являются внешними углами треугольника, и их сумма также будет равна 360 градусов.
Таким образом, для данного примера сумма внешних углов треугольника ABC будет равна 360 градусов.
Пример 2: четырехугольник
Рассмотрим пример четырехугольника и вычислим сумму его внешних углов.
| Углы | Значения |
|---|---|
| Угол A | 60° |
| Угол B | 100° |
| Угол C | 80° |
| Угол D | 120° |
Для вычисления суммы внешних углов четырехугольника применим формулу: S = 360° - (A + B + C + D).
Подставим значения углов в формулу: S = 360° - (60° + 100° + 80° + 120°).
Выполняя вычисления, получим результат: S = 360° - 360° = 0°.
Таким образом, сумма внешних углов четырехугольника равна 0°.
Пример 3: пятиугольник
Рассмотрим пример пятиугольника. Пятиугольник, как следует из названия, имеет пять углов. Для расчета суммы внешних углов этого многоугольника можно воспользоваться формулой:
Сумма внешних углов = 360 градусов
Используя данную формулу, можно получить сумму внешних углов пятиугольника, которая равна 360 градусов.
Например, если внешний угол пятиугольника равен 60 градусов, то сумма всех внешних углов составит:
Сумма внешних углов = 60° + 60° + 60° + 60° + 60° = 300°
Таким образом, в примере пятиугольника с углом 60 градусов, сумма всех внешних углов составит 300 градусов.
Пример 4: шестиугольник
Каждый внешний угол шестиугольника равен 360 градусов деленное на количество углов, т.е. 360 градусов / 6 углов = 60 градусов.
Таким образом, сумма внешних углов шестиугольника равна 360 градусов.



