В математике, вопросы, связанные с углами, всегда представляют особый интерес. Один из таких вопросов - сумма противоположных углов вписанного четырехугольника. Эта тема является одной из базовых концепций геометрии и имеет большое значение при решении различных задач.
Чтобы понять, как вычислять сумму противоположных углов в вписанном четырехугольнике, необходимо знать несколько правил. Первое правило заключается в том, что сумма всех углов в любом четырехугольнике равна 360 градусов. Это свойство можно использовать для расчета суммы противоположных углов.
Во-вторых, сумма углов, противолежащих друг другу, всегда равна 180 градусов. Например, если в вписанном четырехугольнике углы A и C являются противоположными, то их сумма будет равна 180 градусов.
Рассмотрим пример. Пусть у нас есть вписанный четырехугольник ABCD, в котором углы A и C являются противоположными. Известно, что угол А равен 70 градусов. В этом случае, сумма углов A и C будет равна 180 градусам. Зная значение угла A, мы можем вычислить значение угла C, исходя из формулы: C = 180 - A. Таким образом, если угол А равен 70 градусам, то угол C будет равен 180 - 70 = 110 градусам.
Сумма углов в вписанном четырехугольнике

Сумма углов в вписанном четырехугольнике равна 360 градусов. Это свойство можно доказать различными способами.
Во-первых, в вписанном четырехугольнике каждая сторона пересекает окружность, а углы, образованные этими сторонами, равны половине измененной дуги. Таким образом, сумма этих углов будет равна сумме длин измененных дуг, которая составляет 360 градусов.
Во-вторых, можно использовать свойство теоремы о сумме углов треугольника. В вписанном четырехугольнике можно провести две диагонали, получив два треугольника внутри него. Сумма углов обоих треугольников будет равна 180 градусов, поэтому сумма углов в вписанном четырехугольнике будет равна 360 градусов.
Таким образом, сумма углов в вписанном четырехугольнике всегда равна 360 градусов, независимо от его формы и размера углов.
Определение и свойства
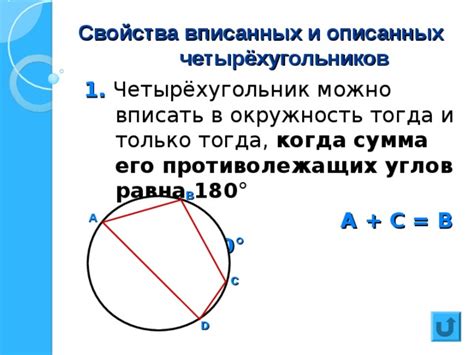
Одним из основных свойств вписанного четырехугольника является то, что сумма противоположных углов всегда равна 180 градусам. Это свойство можно легко доказать, применив теорему о сумме углов внутри треугольника.
Для вписанного четырехугольника ABCD сумма противоположных углов равна:
∠A + ∠C = ∠B + ∠D = 180°
Это свойство может быть использовано для нахождения неизвестных углов вписанного четырехугольника, если известны другие углы.
Вписанный четырехугольник также обладает следующими свойствами:
- Сумма углов данного четырехугольника всегда равна 360 градусам.
- Продолжение сторон вписанного четырехугольника пересекает окружность в дополнительных точках, которые также лежат на окружности.
- Противоположные углы вписанного четырехугольника являются смежными углами двух взаимно-обратных полуокружностей, которые определяются этими углами.
Формула для вычисления суммы противоположных углов

Сумма противоположных углов в вписанном четырехугольнике может быть вычислена с помощью следующей формулы:
Сумма противоположных углов = 180°
Эта формула основана на свойстве вписанного четырехугольника, согласно которому сумма углов, образованных диагоналями, равна 360°. Поскольку четырехугольник вписан в окружность, сумма противоположных углов будет составлять половину от суммы углов на основе.
Например, если один из углов вписанного четырехугольника равен 70°, то сумма противоположных углов будет равна 180° - 70° = 110°. Таким образом, второй противоположный угол также будет равен 110°.
Формула для вычисления суммы противоположных углов вписанного четырехугольника является полезным инструментом при решении геометрических задач и может быть применена для определения углов в различных конструкциях и фигурах.
Важная особенность вписанных четырехугольников
Такая особенность вписанных четырехугольников открывает множество возможностей для решения геометрических задач. Зная значение одного угла, можно легко найти измерение противоположного угла и использовать эту информацию для нахождения других неизвестных величин.
Сумма противоположных углов вписанного четырехугольника может быть полезной при построении графических представлений и моделей, а также при решении задач, связанных с углами и их отношениями.
Приведем пример: рассмотрим вписанный четырехугольник ABCD, в котором известны углы A и C. Применяя свойство суммы противоположных углов, можно легко найти значение углов B и D. Если, например, A = 50° и C = 70°, то B = 180° - A = 180° - 50° = 130° и D = 180° - C = 180° - 70° = 110°.
Таким образом, зная значение только двух углов, можно найти измерения всех углов вписанного четырехугольника. Это является полезным инструментом для геометрических рассуждений и анализа.
Примеры вычисления суммы углов

Рассмотрим несколько примеров вычисления суммы углов в вписанном четырехугольнике:
Пример 1:
Дано вписанный четырехугольник ABCD. Известно, что угол BCD равен 100°. Требуется найти сумму углов BAC и BDC.
Решение:
Из свойств вписанного четырехугольника мы знаем, что сумма противоположных углов равна 180°. Значит, угол BAC равен 180° - 100° = 80°.
Также мы можем воспользоваться тем, что сумма всех углов в четырехугольнике равна 360°. Тогда угол BDC равен 360° - 100° = 260°. Следовательно, сумма углов BAC и BDC равна 80° + 260° = 340°.
Пример 2:
Дано вписанный четырехугольник XYZW. Известно, что угол XWZ равен 130°, а угол YXZ равен 75°. Найдем сумму углов ZYX и ZWY.
Решение:
Снова воспользуемся свойствами вписанного четырехугольника. Угол ZYX равен 180° - 75° = 105°.
Аналогично, угол ZWY равен 180° - 130° = 50°.
Таким образом, сумма углов ZYX и ZWY равна 105° + 50° = 155°.
Такие примеры позволяют нам более наглядно представить свойства вписанных четырехугольников и вычислять сумму их углов.
Следствия и применение

Изучение суммы противоположных углов вписанного четырехугольника имеет несколько следствий и применений в геометрии:
1. Сумма противоположных углов вписанного четырехугольника всегда равна 180 градусов. Это свойство позволяет восстановить углы четырехугольника, если известны только два угла.
2. Если сумма противоположных углов равна 180 градусов, то четырехугольник является вписанным.
3. Данное правило помогает в решении задач на построение четырехугольника с заданными углами. Используя данное свойство, можно находить недостающие углы вписанных четырехугольников.
4. Знание суммы противоположных углов четырехугольника является основой для изучения других теорем и свойств в геометрии.
Таким образом, изучение суммы противоположных углов вписанного четырехугольника является важным элементом геометрии и находит применение в решении различных задач.



