Математика – это наука, которая изучает различные аспекты чисел, их свойств и взаимосвязи. Одним из основных понятий в математике является понятие суммы и слагаемого. Эти термины используются для описания операций сложения, которые являются фундаментальными в арифметике.
Сумма представляет собой результат сложения двух и более чисел или выражений. Она обозначается символом "+". Например, сумма чисел 2 и 3 равна 5. Слагаемые - это числа или выражения, которые складываются. В примере суммы 2+3, числа 2 и 3 являются слагаемыми.
Операция сложения в математике имеет свои особенности. Например, сумма слагаемых не зависит от их порядка. Это означает, что результат сложения чисел 2 и 3 будет таким же, как и результат сложения чисел 3 и 2 – в обоих случаях сумма будет равна 5. Кроме того, сумма нуля и любого числа равна этому числу: 0+5=5. Слагаемые также могут быть отрицательными числами, например, 2+(-3)=-1.
Сумма и слагаемое используются не только в арифметике, но и в других областях математики, таких как алгебра и математический анализ. Понимание этих понятий является базовым для работы с числами и решения различных задач, где требуется сложение и вычисление суммы.
Сумма и слагаемое в математике

Сумма – это результат сложения двух или более чисел. Она показывает общую величину, полученную в результате объединения нескольких значений.
Слагаемое – это одно из чисел, которое складывается с другими для получения суммы. Слагаемые могут быть как положительными (+), так и отрицательными (-).
Процесс сложения основан на свойствах слагаемых:
- Коммутативность: порядок слагаемых не влияет на сумму;
- Ассоциативность: сумма не зависит от расстановки скобок при сложении;
- Существование нейтрального элемента: любое число, при сложении с ним, не меняет своего значения;
- Существование обратного элемента: для каждого числа существует такое число, при сложении с которым дает нейтральный элемент.
Сумма и слагаемое широко используются в различных областях математики, физики, экономики и других наук. Они позволяют проводить анализ, моделирование и решение различных проблем и задач.
Слагаемое - основные понятия

Сумма - это результат операции суммирования двух или более слагаемых. В математике слагаемое даёт вклад в общую сумму. Например, в выражении "a + b" слагаемые a и b суммируются.
Каждое слагаемое может быть представлено как число, переменная или выражение. Например, в выражении "3 + x" число 3 и переменная x являются слагаемыми.
Слагаемые могут быть положительными или отрицательными. В зависимости от их знака, они могут увеличить или уменьшить общую сумму. Например, в выражении "5 + (-3)" число 5 положительное, а число -3 отрицательное.
Основные операции, которые можно применять к слагаемым, включают сложение, вычитание, умножение и деление. Например, в выражении "a + b - c" первые два слагаемых складываются, а затем от них вычитается третье слагаемое.
Использование слагаемых позволяет выполнять арифметические операции с большими числами и сложными выражениями, облегчая работу с числовыми данными.
Для наглядности и более удобного представления слагаемых и суммы, можно использовать таблицу:
| Слагаемое | Сумма |
|---|---|
| a | a + b + c |
| b | |
| c |
Обратите внимание на то, что слагаемые могут быть различной природы: числовыми значениями, переменными или более сложными выражениями.
Сумма чисел - что это такое?
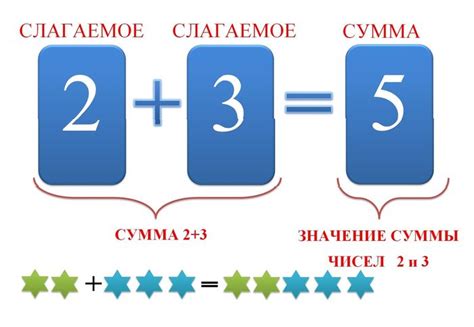
Слагаемые - это числа, которые складываются для получения суммы. Они могут быть как положительными, так и отрицательными. Например, в выражении "2 + 3", числа 2 и 3 являются слагаемыми, а сумма равна 5.
Сумма чисел может быть использована для решения различных задач, например, подсчета общей суммы денег, объединения результатов измерений или нахождения среднего значения. Она также является основой для других математических операций, таких как вычитание, умножение и деление.
Подведение итогов - нужно ли искать сумму чисел?
Например, подсчет суммы может быть полезным, когда нужно определить общее количество элементов или единиц в некотором наборе. Это может быть применено в таких областях как экономика, статистика, физика и другие.
Вычисление суммы чисел также может быть полезным, когда необходимо определить среднее значение или общую сумму, если изначально известны только отдельные значения. Это может быть полезно при анализе данных, например, в финансовых отчетах или определении среднего времени выполнения задачи.
Подсчет суммы чисел может помочь не только в анализе данных, но и в повседневной жизни. Например, можно подсчитать общую стоимость покупок в магазине или определить, сколько времени заняло выполнение задач на доме.
Однако не всегда необходимо искать сумму чисел. В некоторых случаях это может быть бесполезным или невозможным. Например, в некоторых задачах может потребоваться нахождение разности, произведения или частного чисел, а не их суммы. Также, в определенных ситуациях, подсчет суммы может быть затруднен из-за большого объема данных или некорректного представления значений.
Итак, подведение итогов и поиск суммы чисел является важной и полезной операцией в математике и анализе данных. Оно может помочь в определении общего количества или значения набора чисел, а также в вычислении среднего значения или общей суммы. Однако не всегда необходимо искать сумму, и в некоторых случаях это может быть бесполезным или невозможным.
Базовые правила сложения чисел

В математике существуют несколько правил и свойств, которые помогают нам совершать сложение чисел правильно:
1. Коммутативность
Правило коммутативности говорит нам, что порядок слагаемых не влияет на результат сложения. Например, 2 + 3 = 3 + 2.
2. Ассоциативность
Правило ассоциативности говорит нам, что результат сложения трех или более чисел не зависит от того, какой парой чисел мы начнем сложение. Например, (4 + 5) + 6 = 4 + (5 + 6).
3. Ноль
Правило нулевого элемента гласит, что если к числу прибавить 0, результат будет равен этому числу. Например, 7 + 0 = 7. То есть, 0 является нейтральным элементом относительно сложения.
4. Обратное число
Для каждого числа существует обратное число, такое что их сумма равна 0. Например, 4 + (-4) = 0.
С помощью этих правил мы можем производить сложение чисел и получать правильные результаты.
Математический смысл сложения

Сумма - это результат сложения. В выражении "а + б = с", где "а" и "б" являются слагаемыми, а "с" - суммой, слагаемые считаются частями, которые мы собираем или объединяем вместе.
Сложение можно интерпретировать в различных ситуациях. Например, если мы имеем 3 яблока и добавляем к ним еще 5 яблок, то общее количество яблок будет равно 8. В этом случае 3 и 5 являются слагаемыми, а 8 - суммой.
Также сложение можно представить на числовой оси. Если у нас есть точка на числовой оси, и нам нужно переместиться на 3 единицы вправо, а затем на 5 единиц вправо, то итоговая позиция будет находиться на расстоянии 8 единиц от исходной точки. В этом случае 3 и 5 являются слагаемыми, а 8 - суммой.
Сложение также можно представить с помощью операционной модели, где объекты или числа комбинируются и создают новый объект или число.
В математике сложение обладает несколькими свойствами. Например, свойство коммутативности позволяет менять порядок слагаемых без изменения суммы. То есть "а + б" равно "б + а". Еще одно свойство - ассоциативность - позволяет изменять порядок складывания нескольких слагаемых без изменения суммы. То есть "(а + б) + с" равно "а + (б + с)".
Математический смысл сложения направлен на объединение или комбинацию чисел и объектов в одно целое. Сложение имеет множество применений и используется в различных областях науки и повседневной жизни.
Примеры сложения в повседневной жизни

Примеры сложения в повседневной жизни включают:
- Когда несколько человек собираются деньги на общий подарок или оплату счета в ресторане. Каждый вносит свою долю, и все сборы складываются для достижения общей суммы.
- Ежедневное проведение финансового учета. Например, при подсчете расходов за день или месяц, мы складываем все суммы, потраченные на разные товары и услуги.
- Расчет времени. Например, если мы знаем, сколько часов занимает одна задача, а у нас есть несколько задач, мы можем сложить время выполнения каждой задачи, чтобы узнать общее время, необходимое для их выполнения.
- Приготовление пищи. Добавление ингредиентов с указанием определенных весов или объемов, чтобы получить требуемое количество продукта или определенный вкусовой эффект.
Выполняя такие простые задачи, мы применяем основные математические навыки и понимаем, насколько важна операция сложения в повседневной жизни.
Важность сложения в науке и технике

В науке сложение используется для обработки данных и проведения различных вычислений. Например, в физике сложение используется для комбинирования сил, скоростей и других физических величин. В химии сложение используется для расчета расходов реагентов и определения итоговых свойств соединений.
В технике сложение играет значительную роль при проектировании и создании различных устройств и систем. Например, в электротехнике сложение используется для определения общего сопротивления в электрической цепи и расчета суммарной мощности потребляемой энергии. В программировании сложение используется для суммирования значений переменных и выполнения различных математических операций.
Сложение также является базовым элементом для понимания и работы с другими математическими операциями, такими как вычитание, умножение и деление. Без понимания и правильного использования сложения, невозможно эффективно решать математические и научные задачи.
Таким образом, понимание и использование сложения в науке и технике является необходимым для развития знаний и применения математических принципов в практических задачах. Без сложения не было бы ни современной науки, ни инновационных технологий, которые мы используем в повседневной жизни.
Значение сложения в развитии детей

Сложение помогает детям развивать навыки в области математики, логики и абстрактного мышления. Когда дети складывают числа, они учатся анализировать, сравнивать и синтезировать информацию. Они также учатся использовать логические операции, такие как сложение, чтобы решать проблемы и находить решения.
Основы сложения учат детей не только математическим навыкам, но и помогают развивать их общие навыки. Сложение требует внимания к деталям, концентрации и умения извлекать нужную информацию из задачи. Эти навыки являются важными в жизни и других сферах обучения, таких как чтение, письмо и решение проблем.
Сложение также помогает детям развить понимание концепции количества. Когда дети складывают числа, они начинают понимать, что сумма представляет собой новое количество, которое больше, чем исходные числа. Это понимание позволяет детям увидеть связь между абстрактными числами и конкретными объектами или событиями в реальном мире.
В процессе изучения сложения дети также учатся различать слагаемое и сумму. Слагаемые - это числа, которые складываются, а сумма - это результат сложения. Понимание этой разницы помогает детям анализировать задачи и решать их более эффективно.
| Польза сложения в развитии детей | Объяснение |
|---|---|
| Развитие математических навыков | Сложение помогает детям развивать навыки в области математики, логики и абстрактного мышления. |
| Развитие общих навыков | Сложение требует внимания к деталям, концентрации и умения извлекать нужную информацию из задачи. |
| Понимание концепции количества | Сложение помогает детям понять, что сумма представляет собой новое количество, которое больше, чем исходные числа. |
| Различие между слагаемыми и суммой | Понимание разницы между слагаемыми и суммой помогает детям анализировать задачи и решать их. |



