Шестнадцатеричная система счисления – одна из наиболее распространенных систем, используемых в информатике и программировании. В основе этой системы лежит использование шестнадцати цифр: от 0 до 9 и от A до F.
Сложение чисел в шестнадцатеричной системе счисления происходит по тем же правилам, что и в десятичной системе. Однако, в шестнадцатеричной системе нужно учесть особенность с использованием шестнадцати цифр. Например, для сложения чисел A6 и 4F результатом будет число F5.
Важно знать, что при сложении чисел в шестнадцатеричной системе возможно появление дополнительной разрядности – разряда, который «вылезает» за пределы обычного двузначного числа. В этом случае нужно учесть его и прибавить к следующему разряду.
Шестнадцатеричная система счисления активно применяется в программировании, так как позволяет легко и удобно работать с двоичными данными. Например, при работе с цветами в графике или при работе с памятью компьютера.
Сумма чисел в шестнадцатеричной системе
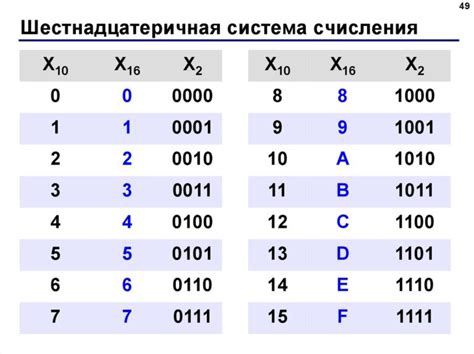
При работе с числами в шестнадцатеричной системе, иногда требуется выполнить их сложение. Для этого необходимо привести числа к одинаковой длине, добавив нули слева, если необходимо. Затем выполняется сложение цифр, начиная с младших разрядов. Если сумма цифр больше основания системы (16), то остаток от деления на 16 берется в качестве новой цифры, а единица переносится в старший разряд.
Например, для сложения чисел A5 и 1F4 в шестнадцатеричной системе счисления:
A5 + 1F4 ------ 299
Таким образом, сумма чисел A5 и 1F4 равна 299 в шестнадцатеричной системе.
Сложение чисел в шестнадцатеричной системе может быть полезным при программировании, особенно когда требуется работать с цветами или адресами памяти, которые обычно представляются в виде шестнадцатеричных чисел.
Особенности суммирования
Суммирование чисел в шестнадцатеричной системе счисления имеет некоторые особенности, которые следует учитывать при работе с ней.
1. Размерность чисел. Шестнадцатеричная система счисления использует 16 различных символов от 0 до 9 и от A до F. Это позволяет представить более широкий диапазон чисел, чем в десятичной системе счисления.
2. Необходимость правильного выравнивания. При сложении чисел разных размеров в шестнадцатеричной системе счисления необходимо правильно выравнивать их, добавляя нули в начало числа с меньшей разрядностью. Это позволяет правильно выполнять операцию сложения.
3. Правила сложения символов. В шестнадцатеричной системе счисления каждому шестнадцатеричному символу соответствует определенное десятичное значение. Для выполнения сложения необходимо правильно соотнести символы и их значения.
4. Перенос разряда. При сложении чисел в шестнадцатеричной системе счисления может возникнуть перенос разряда. Это происходит, когда сумма символов в одном разряде превышает 15. В этом случае переносится единица в следующий разряд.
5. Использование арифметических операций. Для выполнения операций сложения и переноса разряда в шестнадцатеричной системе счисления можно использовать аналогичные арифметические операции в десятичной системе, но с учетом особенностей символов и их значений.
Учитывая эти особенности, можно успешно выполнять операцию сложения чисел в шестнадцатеричной системе счисления и получать правильный результат.



