Средняя линия трапеции — определение, свойства и применение в геометрии

Трапеция – это геометрическая фигура, которая имеет четыре стороны, две из которых параллельны. Самая простая формула, позволяющая вычислить площадь трапеции, основывается на знании ее боковых сторон и высоты, спущенной на одну из параллельных сторон. Однако помимо площади, существуют и другие характеристики трапеции, которые могут быть полезны при решении геометрических задач. Одной из таких характеристик является средняя линия трапеции.

Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон. Это означает, что каждая из двух боковых сторон трапеции делится на две равные части, и средняя линия является отрезком, соединяющим середины этих равных частей. Еще один способ понять сущность средней линии трапеции – это представить трапецию, как сумму двух треугольников. Средняя линия трапеции является основанием для этой суммы.

Средняя линия трапеции обладает рядом интересных свойств. Например, она параллельна основаниям трапеции и равна половине суммы этих оснований. Это означает, что если мы знаем длины оснований трапеции, мы можем легко вычислить длину ее средней линии. И наоборот, если мы знаем длину средней линии и одно из оснований трапеции, мы можем найти длину второго основания. Кроме того, средняя линия трапеции также является высотой для параллелограмма, образованного продолжением боковых сторон трапеции.

Средняя линия трапеции: определение и свойства

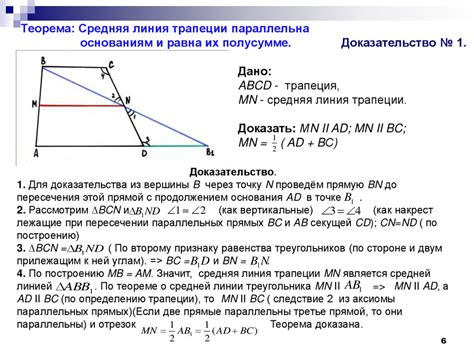
Средняя линия трапеции имеет несколько интересных свойств:

1. Длина средней линии равна среднему арифметическому длин оснований. Если длины оснований трапеции равны a и b, то длина средней линии будет равна (a + b) / 2.
2. Средняя линия делит трапецию на две равные площади.
3. Средняя линия является осью симметрии для трапеции. Это означает, что отрезки, соединяющие точки пересечения средней линии с боковыми сторонами, имеют равные длины.
4. Средняя линия параллельна основаниям трапеции.
5. Если средняя линия трапеции перпендикулярна одному из оснований, то она перпендикулярна и другому основанию.

Знание, понимание и использование свойств средней линии трапеции позволяет решать разнообразные задачи геометрии, связанные с трапециями и их свойствами.

Средняя линия трапеции: что это?

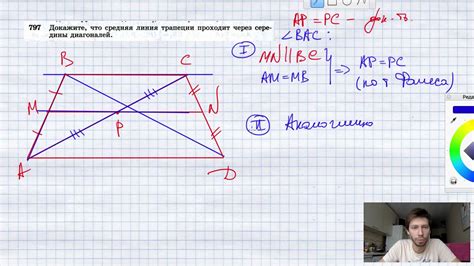
Средняя линия трапеции делит ее на две равные по площади трапеции. Это значит, что площадь каждой из этих трапеций равна половине площади исходной трапеции.

Средняя линия трапеции также играет важную роль при вычислении периметра и площади трапеции. Например, чтобы найти периметр трапеции, можно сложить длины всех ее сторон, включая среднюю линию.

В геометрическом построении трапеции, средняя линия является важным элементом для определения и анализа свойств этой фигуры. Она обладает рядом уникальных свойств и может использоваться для выведения других геометрических закономерностей и теорем, связанных с трапецией.

Свойства средней линии трапеции

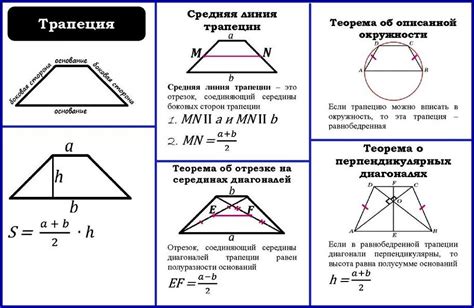
Свойства средней линии трапеции:

1. Средняя линия трапеции делит трапецию на две равные по площади трапеции.
2. Средняя линия трапеции равна полусумме длин оснований трапеции.
3. Средняя линия трапеции параллельна основаниям трапеции.
4. Средняя линия трапеции является осью симметрии трапеции.

Используя эти свойства, можно решать задачи, связанные с нахождением площади и длины средней линии трапеции, а также другие задачи, в которых требуется знание свойств этой линии. Средняя линия трапеции является важным элементом геометрии и находит применение в различных областях науки и практики.

Формула вычисления средней линии трапеции

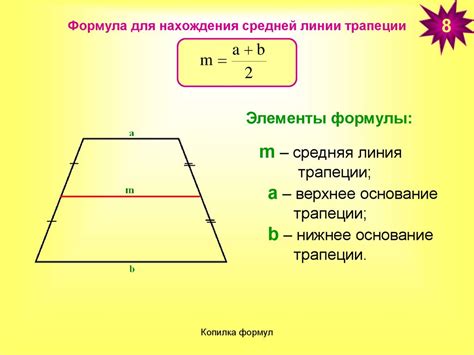
Формулу вычисления длины средней линии трапеции можно записать следующим образом:

L_ср = (a + b) / 2

где L_ср - длина средней линии трапеции, a и b - длины параллельных сторон трапеции.

Эта формула утверждает, что средняя линия трапеции равна полусумме длин ее параллельных сторон.

Используя данную формулу, легко вычислить длину средней линии трапеции, зная длины ее параллельных сторон.