Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны друг другу. Однако, чтобы убедиться, что параллелограмм лежит в плоскости, необходимо выполнить несколько проверок.
Во-первых, можно рассмотреть диагонали параллелограмма. Если диагонали пересекаются в одной точке, то это является доказательством того, что параллелограмм лежит в одной плоскости. Если же диагонали не пересекаются или пересекаются в разных точках, то параллелограмм не лежит в плоскости.
Во-вторых, можно визуально оценить параллелограмм. Если все его стороны и углы находятся в одной плоскости, то это дополнительное подтверждение того, что фигура является параллелограммом, лежащим в плоскости. Кроме того, можно использовать геометрические конструкции и формулы для доказательства, что все углы и стороны параллелограмма лежат в одной плоскости.
Важно отметить, что для точного доказательства, что параллелограмм лежит в плоскости, необходимо провести все вышеперечисленные проверки и убедиться, что все условия выполняются.
Невозможность извлечь параллелограмм, васельки, из куба
Рассмотрим параллелограммы с различными свойствами:
| Свойство параллелограмма | Возможность извлечения из куба |
|---|---|
| Прямоугольник | Да |
| Ромб | Да |
| Квадрат | Да |
| Произвольный параллелограмм | Нет |
Как видно из таблицы, все прямоугольники, ромбы и квадраты можно получить из куба путем вырезания его граней и их последующего соединения. Однако, произвольный параллелограмм невозможно получить из куба, так как его стороны не будут параллельными граням куба.
Параллелограммы в плоскости
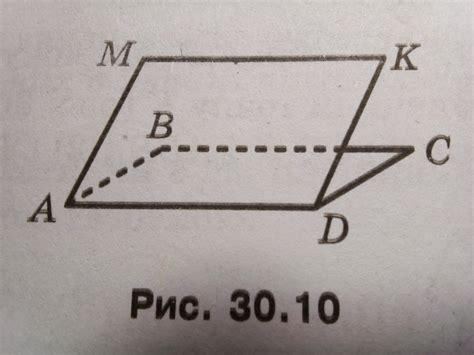
Для того чтобы доказать, что параллелограмм лежит в плоскости, можно воспользоваться несколькими способами:
1. Геометрическое доказательство:
Рассмотрим произвольный параллелограмм ABCD. Проведем диагонали AC и BD. Заметим, что в треугольнике ABC и треугольнике BCD угол ABC и угол BCD являются вертикальными, а значит, они равны между собой. Также у нас есть параллельные прямые AB и DC, и поэтому угол BAC равен углу ACD. Следовательно, угол ABC и угол ACD являются параллельными, что означает, что треугольник ABC лежит в одной плоскости с треугольником BCD. А поскольку параллелограмм ABCD состоит из этих треугольников, то он также лежит в одной плоскости.
2. Векторное доказательство:
Рассмотрим векторы AB, BC и CD, их сумма равна нулю: AB + BC + CD = 0. Это означает, что эти векторы лежат в одной плоскости. Также заметим, что AB и CD - это диагонали параллелограмма, и поскольку их сумма равна нулю, значит, эти диагонали лежат в одной плоскости. Далее, зная, что параллельные прямые имеют равные направляющие векторы, получаем, что стороны параллелограмма AB и CD лежат в одной плоскости. Таким образом, все стороны параллелограмма лежат в одной плоскости, а значит и сам параллелограмм лежит в одной плоскости.
В результате, мы получаем, что любой параллелограмм лежит в одной плоскости, что является необходимым условием его определения. Это свойство используется при решении геометрических задач, связанных с параллелограммами.
Геометрические особенности параллелограмма
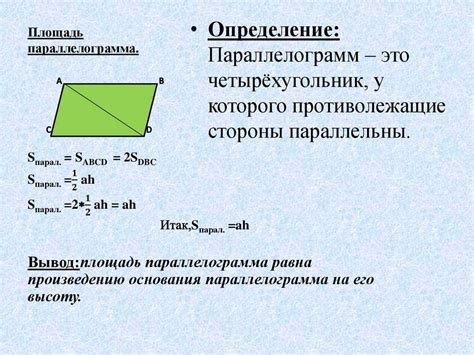
- У параллелограмма все углы равны между собой и составляют 180 градусов.
- Оппозитные стороны параллелограмма равны по длине. Это означает, что если одну сторону параллелограмма увеличить или уменьшить, то соответствующая ей противоположная сторона также изменится на то же самое значение.
- Диагонали параллелограмма делят его на два равных треугольника. Это свойство является следствием того факта, что противоположные стороны параллелограмма параллельны друг другу.
- Диагонали параллелограмма также являются взаимно перпендикулярными, то есть пересекаются под прямым углом.
- Площадь параллелограмма можно вычислить, используя формулу: площадь = длина стороны × высота, где высота – это перпендикуляр, опущенный из вершины на противоположную сторону.
Знание этих геометрических особенностей позволяет более полно понять структуру и свойства параллелограмма, а также применять их для решения геометрических задач.
Алгебраические свойства параллелограмма

| Свойство | Алгебраическое обоснование |
|---|---|
| Противоположные стороны равны | Если параллелограмм ABCD, то AB = CD и AD = BC. Для доказательства этого свойства можно использовать координатную плоскость и алгебраические формулы для длин отрезков. |
| Диагонали делятся пополам | Если параллелограмм ABCD, то точка пересечения диагоналей M, будет являться серединой обеих диагоналей AC и BD. Это можно доказать, используя свойства векторов и алгебраические операции. |
| Сумма квадратов длин сторон равна сумме квадратов диагоналей | Если параллелограмм ABCD, то AB^2 + BC^2 + CD^2 + AD^2 = AC^2 + BD^2. Для доказательства этого свойства можно использовать координатную плоскость и алгебраические формулы для длин отрезков. |
| Соседние углы параллелограмма суммируются в 180 градусов | Если параллелограмм ABCD и угол А равен Ү, то угол B будет равен 180 - Ү. Для доказательства этого свойства можно использовать геометрические и алгебраические методы. |
Эти алгебраические свойства помогают доказать равенства и отношения внутри параллелограмма и использовать его в решении математических задач и задач геометрии.
Способы доказательства параллелограмма в плоскости
- Доказательство по определению. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны. Для того чтобы доказать, что фигура является параллелограммом, необходимо проверить, что противоположные стороны данной фигуры параллельны.
- Доказательство с помощью векторов. Параллелограмм может быть доказан с использованием векторных свойств. Для этого необходимо проверить, что векторы, соединяющие противоположные вершины данного четырехугольника, равны по модулю и имеют одинаковое направление.
Используя указанные способы, можно доказать, что заданный четырехугольник является параллелограммом и лежит в плоскости.
Доказательства основных свойств параллелограмма
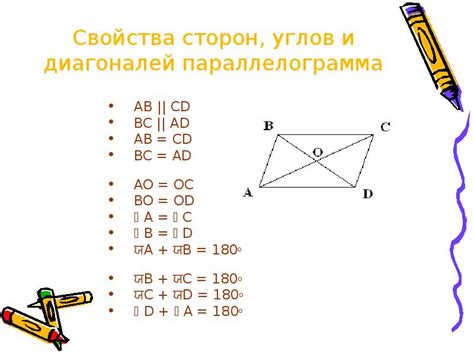
Доказательство свойств параллелограмма можно провести с использованием различных методов и теорем. Рассмотрим некоторые из них:
| Свойство | Доказательство |
| Противоположные стороны параллельны | Используем перпендикулярную диагональную теорему: если в четырехугольнике диагонали перпендикулярны, то стороны, образованные данными диагоналями, параллельны. |
| Противоположные стороны равны | Используем доказательство равенства треугольников: проводим диагонали, получаем два треугольника и доказываем их равенство по сторонам и углам. |
| Противоположные углы равны | Используем доказательство равенства треугольников: проводим диагонали, получаем два треугольника и доказываем их равенство по сторонам и углам. |
| Диагонали взаимно делятся пополам | Используем доказательство геометрической средней пропорции: проводим диагонали, получаем два треугольника и доказываем, что отношение отрезков, на которые диагонали делят друг друга, равно 1. |
Таким образом, с использованием перпендикулярной диагональной теоремы, доказательства равенства треугольников и доказательства геометрической средней пропорции, можно убедиться в достоверности основных свойств параллелограмма.
Применение параллелограмма в математике и физике
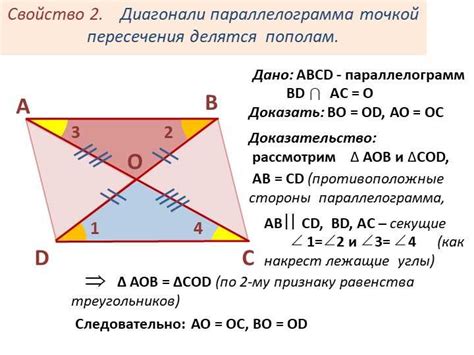
В математике параллелограмм используется для изучения свойств и характеристик разных объектов. Например, векторы в трехмерном пространстве могут быть представлены с помощью параллелограмма, где стороны параллелограмма соответствуют векторам. Также параллелограмм используется для доказательства различных теорем. Например, чтобы доказать, что серединные перпендикуляры к сторонам параллелограмма пересекаются в одной точке, можно использовать свойства параллелограмма.
В физике параллелограмм используется для моделирования сил и векторов. Силы могут быть представлены с помощью векторов, которые образуют параллелограмм. Таким образом, параллелограмм позволяет наглядно представить и анализировать различные физические явления и процессы. Например, при анализе сил, действующих на тело, можно использовать параллелограмм для определения результирующей силы и ее направления.
Таким образом, параллелограмм является важным инструментом в математике и физике, которым можно моделировать и изучать разные объекты и явления. Его свойства и характеристики позволяют решать различные задачи и доказывать теоремы.



