Смежные углы - это углы, имеющие общую сторону и одну общую вершину. Такие углы возникают, когда две прямые линии пересекаются или когда одна прямая линия пересекает две параллельные прямые. Интересует ли вас равенство этих углов?
Мы знаем, что смежные углы могут быть равными или неравными. Это зависит от разных условий и свойств геометрической фигуры или системы прямых. Но существуют некоторые общие правила, которые помогут вам определить равенство смежных углов.
Например, если две прямые линии пересекаются и образуют угол, то любые два смежных угла будут дополнительными друг к другу. То есть, если один угол равен 40 градусам, то второй смежный угол будет равен 140 градусам. Также существуют правила для параллельных прямых и других сложных систем прямых.
Смежные углы в геометрии: определение и свойства

Смежные углы образуются двумя прямыми, которые пересекаются, и могут обладать разными свойствами. Рассмотрим основные свойства смежных углов:
- Сумма смежных углов равна 180 градусов. Это следует из того, что при пересечении двух прямых линий образуется две пары смежных углов, которые в сумме дают прямой угол.
- Если один из смежных углов является прямым углом (равен 90 градусам), то другой смежный угол также будет прямым углом.
- Если один из смежных углов является острым (меньше 90 градусов), то другой смежный угол будет тупым (больше 90 градусов).
- Смежные углы могут быть равными, если они имеют одинаковые величины и одинаковые типы (острые, прямые, тупые).
Смежные углы широко используются в геометрии при решении задач на нахождение неизвестных углов. Понимание и применение свойств смежных углов значительно облегчает анализ и решение таких задач.
Смежные углы: основные типы и примеры
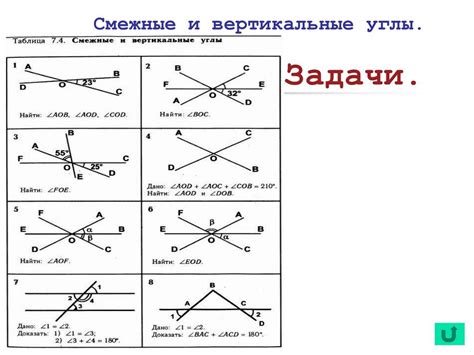
Основные типы смежных углов:
1. Смежные углы, образованные пересекающимися прямыми:
Два угла, образованных пересекающимися прямыми, их продолжениями и прямым углом, называются "вертикальными". Например, если имеется два одинаковых угла, расположенных по обе стороны вертикальной прямой, то они являются вертикальными смежными углами.
2. Смежные углы, созданные пересечением двух параллельных прямых:
Два угла, образованных пересекающимися прямыми и параллельными прямыми, называются "сопряженными внутренними" или "сопряженными внешними". Например, если имеется две параллельные прямые и угол на одной из них, а также два угла на другой прямой, то углы на одной прямой будут являться сопряженными внутренними углами, а углы на другой прямой – сопряженными внешними.
3. Смежные углы, образованные пересечением касательной и хорды окружности:
Два угла, образованных пересечением касательной и хорды окружности, называются "смежными на окружности". Например, если имеется окружность и касательная, а также угол, образованный хордой и касательной, то этот угол будет смежным на окружности с другими углами, образованными хордой и касательной или их продолжениями.
Примеры смежных углов:
1. Имеется пересекающиеся прямые AB и CD. В этом случае два угла 1 и 3, а также два угла 2 и 4, будут вертикальными смежными углами.
2. Есть две параллельные прямые AB и CD. В этом случае два угла 1 и 2, а также два угла 3 и 4, будут сопряженными внутренними углами.
3. Существует окружность с касательной AB и хордой CD. В этом случае угол 1, образованный хордой и касательной, будет смежным на окружности с углами 2 и 3.
Таким образом, смежные углы могут принимать разные формы и быть представлены различными комбинациями угловых элементов. Изучение смежных углов позволяет лучше понять и описать геометрические взаимосвязи и свойства различных фигур и форм.
Смежные углы: условия равенства
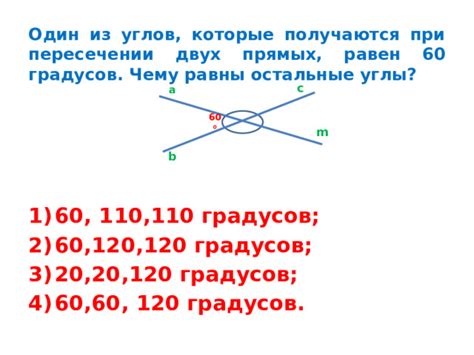
Углы являются равными, если они удовлетворяют определенным условиям:
1. Углы должны быть смежными: это значит, что они должны иметь общую сторону и быть расположены по разные стороны от нее.
2. Углы должны быть вертикальными: если углы расположены на пересекающихся прямых линиях и имеют одну и ту же меру, то они являются смежными углами и, следовательно, равными.
3. Углы должны быть дополнительными: если углы расположены на параллельных прямых линиях и их сумма равна 180 градусам, то они являются смежными углами и, следовательно, равными.
4. Углы должны быть зеркальными: если углы расположены на пересекающихся прямых линиях и их меры составляют сумму 180 градусов, то они являются смежными углами и, следовательно, равными.
Зная эти условия, мы можем определить, равны ли смежные углы в данной ситуации. Это очень полезно при решении геометрических задач и доказательств теорем.
Смежные углы и их связь с параллельными прямыми
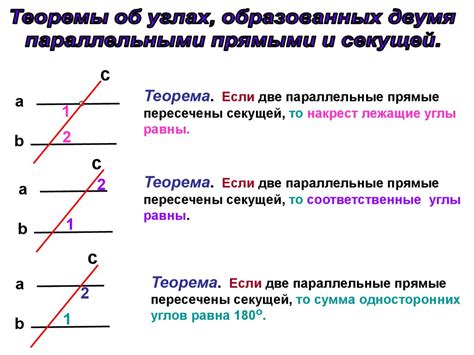
Если две прямые линии параллельны, то смежные углы находятся по разные стороны каждой из двух пересекаемых прямых.
Когда две прямые линии пересекаются третьей прямой, образуются восемь смежных углов. Эти углы могут быть разделены на две пары - внутренние и внешние смежные углы.
| Внутренние смежные углы: | Внешние смежные углы: |
| 1 и 3 | 5 и 7 |
| 2 и 4 | 6 и 8 |
Внутренние смежные углы образуются между двумя пересекаемыми прямыми внутри фигуры. Внешние смежные углы образуются свернутой фигурой вокруг двух пересекаемых прямых.
Основной результат, связывающий смежные углы и параллельные прямые, заключается в том, что внутренние смежные углы, образованные параллельными прямыми и пересекаемой прямой, являются смежными и дополнительными.
То есть, если две прямые линии параллельны, и на них лежит третья пересекающая прямая, то внутренние смежные углы, образованные этими прямыми и пересекающей прямой, являются смежными и дополнительными, то есть их сумма равна 180 градусам.
Смежные углы в повседневной жизни и применение в дизайне
В повседневной жизни мы регулярно сталкиваемся с ситуациями, где смежные углы играют ключевую роль. Например, при декорировании комнаты, мы можем использовать мебель или элементы дизайна смежных углов для создания гармоничного и сбалансированного интерьера. Это может быть поставка двух стульев, которые образуют смежные углы, или использование зеркал с рамами, расположенными под определенным углом. Такие элементы помогают создавать чувство равновесия и гармонии в комнате.
В дизайне смежные углы также имеют важное значение. Их применение может добавить интересности и динамичности к проекту. Например, веб-дизайнер может использовать смежные углы для создания стрелок или прямоугольных форм, которые указывают на важные элементы или действия на веб-странице. Эта техника помогает привлечь внимание пользователя и сделать дизайн более запоминающимся.
Однако, не следует забывать, что смежные углы не всегда равны. Единственное условие для смежных углов – это общая сторона. Следовательно, при использовании смежных углов в дизайне важно учитывать разные размеры и формы этих углов, чтобы достичь желаемого эффекта.



