Многоугольник – это плоская геометрическая фигура, состоящая из трех или более отрезков, которые называются сторонами, и вершин, в которых стыкуются эти отрезки. В многоугольниках могут быть как смежные, так и несмежные отрезки.
Смежные отрезки многоугольника – это отрезки, которые имеют общую вершину и являются соседними. Такие отрезки соединяют две соседние вершины многоугольника, образуя его стороны. Смежные отрезки в многоугольнике имеют общую точку, в которой они сходятся.
Несмежные отрезки многоугольника – это отрезки, которые не имеют общей вершины и не являются соседними. Такие отрезки соединяют вершины многоугольника, которые находятся на определенном расстоянии друг от друга. Несмежные отрезки в многоугольнике не пересекаются и не имеют общих точек.
Знание понятия смежных и несмежных отрезков многоугольника является важным для изучения геометрии и работы с многоугольниками в различных задачах. Это позволяет определить грани и углы многоугольника, а также проводить различные доказательства и вычисления, основываясь на свойствах смежных и несмежных отрезков.
Смежные отрезки многоугольника: определение и свойства
Для понимания смежных отрезков многоугольника необходимо представить себе многоугольник как набор вершин, соединенных сторонами. Каждая сторона многоугольника является отрезком. И если две стороны имеют общую вершину, то эти отрезки называются смежными.
Свойства смежных отрезков многоугольника:
- Сумма длин смежных отрезков многоугольника равна длине соответствующей стороны многоугольника. Например, если смежные отрезки имеют длины 3 и 4, то сторона многоугольника, которую они соединяют, будет иметь длину 7.
- Смежные отрезки многоугольника могут быть как прямыми, так и наклонными. В зависимости от формы многоугольника и положения вершин, смежные отрезки могут образовывать различные углы - острые, прямые или тупые. Эти углы могут быть равными или не равными.
- Смежные отрезки многоугольника не пересекаются внутри многоугольника. Они могут пересекаться только в вершинах многоугольника.
Важно понимать свойства смежных отрезков многоугольника для того, чтобы правильно их использовать при решении геометрических задач и расчетах.
Определение смежных отрезков многоугольника

Смежными отрезками многоугольника называются два отрезка, которые имеют общую точку на границе многоугольника и не пересекаются. Такие отрезки будут иметь конечную точку на одной из вершин многоугольника и продолжаться до соседних вершин.
Смежные отрезки являются частным случаем несмежных отрезков, когда разделяющая их точка находится на границе многоугольника. Важно отметить, что смежные отрезки могут быть как сторонами многоугольника, так и диагоналями, соединяющими вершины многоугольника, в зависимости от конкретной конфигурации фигуры.
Знание понятия смежных отрезков многоугольника играет важную роль при решении задач геометрии и строительства, поскольку позволяет определять взаимное расположение элементов многоугольника, проводить параллельные или перпендикулярные отрезки и выполнять другие операции на плоскости.
Несмежные отрезки многоугольника: значения и свойства
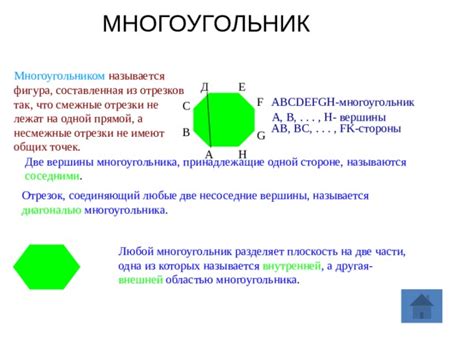
Несмежные отрезки многоугольника - это отрезки, которые не являются соседними и не имеют общей вершины. Они соединяют вершины, которые не являются соседними.
У несмежных отрезков многоугольника иногда есть своеобразные значения и свойства:
1. Диагонали - это вид несмежных отрезков, которые соединяют вершины многоугольника и не являются его сторонами. Диагонали многоугольника имеют особое значение, так как они создают множество дополнительных углов, точек пересечения и линий симметрии.
2. Веревки - это отрезки, которые соединяют вершины многоугольника, но не пересекают его внутреннюю область и не проходят через него. Веревки несмежных вершин многоугольника могут использоваться для создания различных геометрических конструкций.
3. Окружности - это фигуры, состоящие из всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной центральной точки. Несмежные отрезки многоугольника могут быть использованы для построения окружностей, так как они могут служить радиусами или диаметрами для этих фигур.
Важно отметить, что свойства и значения несмежных отрезков многоугольника могут различаться в зависимости от типа многоугольника и его особенностей. Для более точного и подробного описания конкретного многоугольника рекомендуется обратиться к его геометрическим характеристикам и определениям.
Определение несмежных отрезков многоугольника
В многоугольнике любой отрезок, соединяющий две вершины, называется стороной многоугольника. Смежные отрезки - это отрезки, которые имеют общую вершину и расположены рядом друг с другом. Несмежные отрезки - это отрезки, которые не имеют общих вершин и могут быть удалены друг от друга.
Несмежные отрезки многоугольника могут быть полезны для анализа геометрических свойств фигуры. Например, при изучении регулярного многоугольника, все его стороны являются несмежными отрезками.
Важно отметить, что несмежные отрезки многоугольника могут пересекаться или даже быть параллельными, что создает различные конфигурации и возможности для исследования многоугольника.



