Если вы приступили к изучению геометрии, то наверняка сталкивались с понятием внешних углов фигуры. Углы, образованные продолжением сторон фигуры, называются внешними углами. Четырехугольник – это многоугольник, состоящий из четырех сторон и четырех углов. Интересно, что сумма внешних углов четырехугольника всегда равна 360 градусов.
Для нахождения суммы внешних углов четырехугольника существует формула. Чтобы ее понять, важно понимать, что каждый внешний угол четырехугольника образуется продолжением одной из его сторон и смежными внутренними углами. Формула для нахождения суммы внешних углов четырехугольника выглядит так: сумма внешних углов равна 360 градусов.
Представим, что у нас есть четырехугольник ABCD. Сначала найдем все внутренние углы этого четырехугольника (углы BAC, ADC, CDB и BDA). Затем от каждого внутреннего угла отложим отрезок наружу, образуя внешний угол (углы BAD, BCA, CDA и DBC). Если сложить все внешние углы, то получится 360 градусов – полная сумма внешних углов четырехугольника.
Формула суммы внешних углов четырехугольника: результат работы
Сумма внешних углов любого четырехугольника равна 360 градусов. Это означает, что если мы измерим все внешние углы четырехугольника и сложим полученные значения в градусах, то результат всегда будет равен 360 градусов.
Это свойство можно легко продемонстрировать на любом четырехугольнике. Для этого достаточно измерить каждый внешний угол, суммировать полученные значения и убедиться, что итоговая сумма равна 360 градусов.
Формула суммы внешних углов четырехугольника является важным инструментом в геометрии и находит применение при решении различных задач и задачек.
Доказательство формулы суммы внешних углов четырехугольника
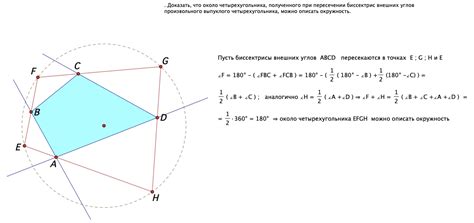
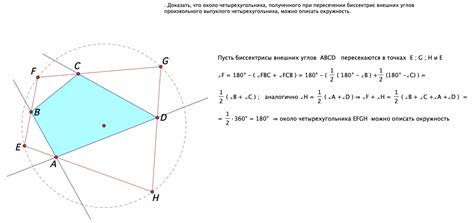
Проведем две дополнительные прямые: AE - продолжение стороны AB, и AF - продолжение стороны AD. Тогда внешний угол A будет смежным с углами E и F.
Заметим, что сумма углов, заключенных в четырехугольнике EAFD, составляет 360 градусов. Это можно легко показать, раскрыв оба угла E и F и суммируя их с углами ABC и ADC, которые образуют прямые углы.
Таким образом, сумма внешних углов четырехугольника ABCD равна сумме углов внешнего четырехугольника EAFD, то есть 360 градусов. Этот результат можно обобщить для любого четырехугольника.
Свойства внешних углов четырехугольника


Внешние углы обозначаются через индексы - α, β, γ и δ.
Свойство внешних углов четырехугольника гласит, что сумма мер всех внешних углов равна 360 градусам. Иными словами, α + β + γ + δ = 360°.
Это свойство позволяет определить значение одного внешнего угла, зная значения остальных. Например, если известны меры углов α, β и γ, то можно найти меру угла δ, вычитая сумму из 360°: δ = 360° - (α + β + γ).
Свойство внешних углов четырехугольника имеет большое значение при решении различных геометрических задач, связанных с четырехугольниками. Оно помогает находить значения углов, определять типы четырехугольников и доказывать различные утверждения о них.
Применение формулы суммы внешних углов четырехугольника в геометрии

Четырехугольник, как известно, состоит из четырех углов. Внешний угол четырехугольника определяется продолжением одной из его сторон за точку соответствующего угла. Формула суммы внешних углов гласит, что сумма внешних углов четырехугольника всегда равна 360 градусам.
Применение этой формулы позволяет решать различные задачи, связанные с четырехугольниками, например:
- Нахождение недостающих углов. Если известны значения трех углов четырехугольника, можно найти четвертый угол, вычитая сумму трех известных углов из 360 градусов.
- Доказательство свойств четырехугольников. Используя формулу суммы внешних углов, можно доказать, например, что сумма углов диагонального четырехугольника равна 360 градусам.
- Решение задач на построение. Зная значение одного или нескольких внешних углов четырехугольника и используя формулу суммы внешних углов, можно решить задачи на построение четырехугольников с заданными углами.
Формула суммы внешних углов четырехугольника является важным инструментом в геометрии и находит применение в различных областях, включая строительство, дизайн, компьютерную графику и прочие.
Важность понимания формулы суммы внешних углов четырехугольника
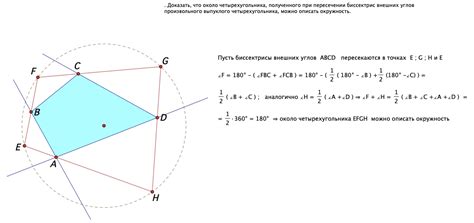
Понимание формулы суммы внешних углов четырехугольника помогает нам решать различные задачи, связанные с геометрией. Например, на основе этой формулы мы можем проверять, является ли данный четырехугольник выпуклым или вогнутым. Если сумма внешних углов равна 360 градусов, то четырехугольник выпуклый. В случае, если сумма внешних углов больше 360 градусов, то четырехугольник вогнутый.
Кроме того, формула суммы внешних углов четырехугольника помогает нам вычислять отдельные углы внешнего многоугольника на основе известных углов. Если, например, мы знаем значения трех внешних углов, то мы можем вычислить четвертый угол, используя формулу суммы внешних углов четырехугольника.
Понимание этой формулы также помогает нам строить и измерять четырехугольники с точностью. Зная сумму внешних углов, мы можем проверять правильность измерений и детектировать возможные ошибки или неточности при построении.
Сравнение формулы суммы внешних углов четырехугольника с другими геометрическими формулами

Одной из таких формул является формула суммы внешних углов четырехугольника. Все четырехугольники имеют сумму внешних углов, равную 360 градусов. Это означает, что если мы измерим угол на каждой вершине четырехугольника и сложим их, мы получим 360 градусов.
Сравнивая формулу суммы внешних углов четырехугольника с другими геометрическими формулами, можно заметить следующее:
| Формула | Описание |
|---|---|
| Сумма внешних углов четырехугольника | Сумма всех углов, образованных продолжениями сторон четырехугольника, равна 360 градусов |
| Формула площади прямоугольника | Площадь прямоугольника равна произведению длин его сторон |
| Формула для нахождения длины окружности | Длина окружности равна произведению диаметра на число π (пи) |
Таким образом, формула суммы внешних углов четырехугольника является одной из множества геометрических формул, которые позволяют вычислить характеристики различных геометрических фигур.
Решение задач с использованием формулы суммы внешних углов четырехугольника
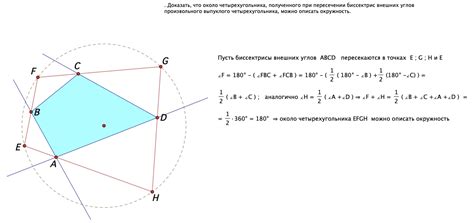
Применение формулы суммы внешних углов четырехугольника помогает решать разнообразные задачи, связанные с этой геометрической фигурой. Вот некоторые примеры возможных задач, в которых можно использовать данную формулу:
- Найти неизвестный внешний угол четырехугольника, если известны все остальные внешние углы.
- Найти периметр четырехугольника, если известны значения всех внешних углов.
- Найти один из внешних углов четырехугольника, если известны значения трех других внешних углов.
- Доказать, что сумма всех внешних углов четырехугольника равна 360 градусов.
Для решения этих задач следует использовать формулу суммы внешних углов четырехугольника:
Сумма внешних углов четырехугольника равна 360 градусов:
Угол1 + Угол2 + Угол3 + Угол4 = 360°
Эта формула позволяет решить задачи, связанные с нахождением внешних углов четырехугольника и определением их суммы. Она основывается на свойстве четырехугольника, которое гласит, что сумма всех его внешних углов равна 360 градусов.
Использование формулы суммы внешних углов четырехугольника позволяет эффективно решать задачи, связанные с этой геометрической фигурой, и обеспечивает точные и надежные результаты. Важно знать и уметь применять данную формулу при решении геометрических задач, связанных с четырехугольниками.
Обобщение формулы суммы внешних углов четырехугольника на n-угольники

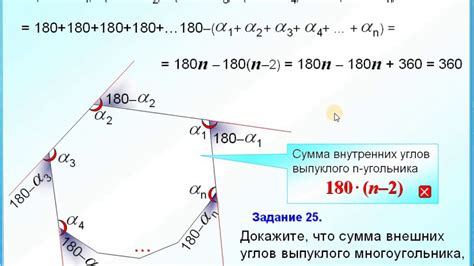
Для доказательства этой формулы можно рассмотреть n-угольник и добавить внешние углы каждой его стороны. Как известно, сумма внешних углов треугольника равна 360 градусам. Каждый следующий угол n-угольника будет добавляться к этой сумме, поэтому сумма внешних углов n-угольника также будет равна 360 градусам.
Это обобщение формулы суммы внешних углов на n-угольники является важным свойством геометрических фигур и применяется при решении различных задач, связанных с многоугольниками.
Мнемоническое правило для запоминания формулы суммы внешних углов четырехугольника
Для запоминания формулы суммы внешних углов четырехугольника можно использовать мнемоническое правило, основанное на первых буквах каждого слова:
- В - Внешние
- У - Углы
- Ч - Четырехугольника
- С - Суммируются
Таким образом, формула суммы внешних углов четырехугольника будет звучать как "ВУЧС" или "ВУЧСК".
Это правило позволяет легко запомнить формулу и использовать ее при решении задач на нахождение суммы внешних углов четырехугольника.
Например, если у нас есть четырехугольник ABCD, то сумма его внешних углов будет равняться 360 градусов (180+90+90).
Как применять формулу суммы внешних углов четырехугольника в повседневной жизни
Для начала, давайте вспомним, что такое внешний угол четырехугольника. Внешний угол образуется при продолжении одной из сторон четырехугольника за пределы фигуры. Другими словами, это угол между прямой, содержащей продолжение одной из сторон, и прямой, содержащей продолжение соседней стороны.
Формула суммы внешних углов четырехугольника гласит, что сумма всех внешних углов равна 360 градусов. То есть, если измерить все внешние углы и сложить их значения, получится ровно 360 градусов.
Как же можно применять эту формулу в повседневной жизни? Например, при работе с картографией или планировании строительства можно использовать данную формулу для вычисления и нахождения углов различных геометрических форм и фигур.
Кроме того, знание формулы суммы внешних углов четырехугольника может быть полезным при решении головоломок и загадок, которые базируются на геометрии и углах. Это может быть интересным способом развлечься и поработать над логическим мышлением.



