Синус - одна из важных геометрических функций, которая широко используется в 8 классе и в дальнейшем в математике.
Синус - это отношение длины противолежащего катета к гипотенузе в прямоугольном треугольнике. Обозначается как sin и выражается с помощью тригонометрического соотношения, где противолежащий катет обозначается буквой a, гипотенуза - буквой c. Таким образом, sin = a/c.
Синус угла - это величина, которая позволяет нам определить, насколько сильно угол отклоняется от вертикальной оси. Синус подразумевает, что у нас есть прямоугольный треугольник, где один из углов является рассматриваемым углом. Мы можем использовать синус для определения высоты полета объекта, угла наклона склона или изменения расстояния между двумя объектами.
Синус в геометрии 8 класс
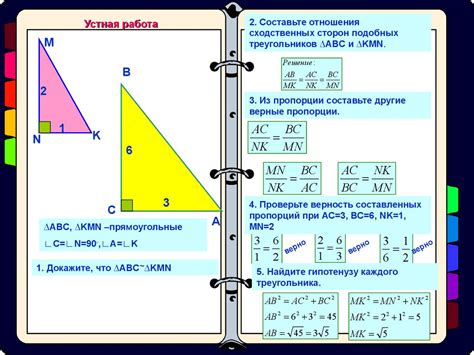
Синус угла определяется как отношение противоположного катета к гипотенузе прямоугольного треугольника. При этом катетом является сторона прямоугольного треугольника, лежащая напротив данного угла, а гипотенузой – сторона, являющаяся гипотенузой.
Восьмиклассники изучают свойства и особенности синуса, находят его значения для разных углов и решают задачи на поиск угла по заданному значению синуса.
- Угол, у которого синус равен 0, имеет меру 0 или 180 градусов.
- Угол, у которого синус равен 1, имеет меру 90 градусов.
- Угол, у которого синус равен -1, имеет меру 270 градусов.
- Значение синуса всегда лежит в интервале от -1 до 1.
- Синус имеет периодические закономерности и повторяет свои значения с определенным шагом.
Знание синуса позволяет эффективно решать задачи, связанные с вычислением расстояний, высот и других параметров треугольников и других геометрических фигур.
Сущность и определение синуса
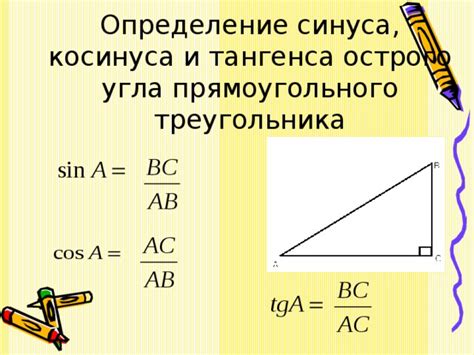
Другими словами, синус угла A (обозначается sin A) равен отношению длины стороны, противолежащей углу A, к длине гипотенузы треугольника, где A – угол, из которого счетчик осуществляется против часовой стрелки.
Формула синуса:
sin A = a / c
где:
- A – угол треугольника;
- a – длина противоположной стороны;
- c – длина гипотенузы.
Значение синуса угла всегда находится в интервале от -1 до 1. Когда синус равен 1, угол является прямым, а когда синус равен 0, угол является прямым. Некоторые основные значения синуса углов: sin 0° = 0, sin 30° = 0.5, sin 45° = 0.707, sin 60° = 0.866, sin 90° = 1.
Синус и соответствующие тригонометрические функции регулярно используются для нахождения длины сторон и измерения углов в геометрии, а также в физике и других науках.
Угол и его характеристики
Углы могут быть острый (меньше 90 градусов), прямой (равен 90 градусам) или тупой (больше 90 градусов). В зависимости от положения сторон относительно друг друга, углы могут быть взаимно дополнительными, смежными, вертикальными или противолежащими.
Синус угла - это отношение противолежащего катета к гипотенузе в прямоугольном треугольнике. Он обозначается как sin.
Синус угла можно вычислить с помощью соответствующей тригонометрической функции. Значение синуса угла может быть от -1 до 1, причем ноль соответствует прямому углу, а единица - острым и тупым углам.
Синус угла имеет множество применений в геометрии, физике, технике и других науках.
Треугольник и его составляющие
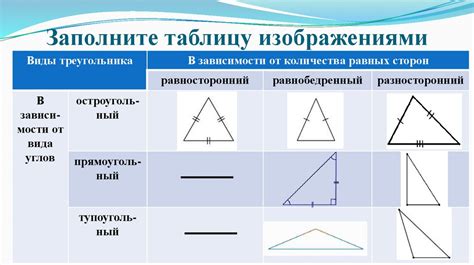
Стороны треугольника обозначаются буквами a, b и c, где a и b - это две произвольные стороны, а c - гипотенуза, находящаяся напротив прямого угла (если треугольник прямоугольный).
Углы треугольника обозначаются буквами A, B и C, где A - угол, находящийся напротив стороны a, B - угол, находящийся напротив стороны b, и C - угол, находящийся напротив стороны c.
Важно отметить, что сумма углов треугольника всегда равна 180 градусов. Это называется свойством внутренних углов треугольника.
Также треугольники могут быть классифицированы по длинам и углам:
- По длинам сторон: равносторонний треугольник, равнобедренный треугольник, разносторонний треугольник.
- По углам: остроугольный треугольник, тупоугольный треугольник, прямоугольный треугольник.
Синус треугольника является одной из тригонометрических функций, которая определена отношением противоположной стороны к гипотенузе в прямоугольном треугольнике.
Треугольник и его составляющие имеют важное значение в геометрии и позволяют решать различные задачи, связанные с расчетами, измерениями и свойствами треугольников.
Теорема синусов и ее применение

Формулировка теоремы синусов звучит следующим образом: в любом треугольнике отношение длины стороны к синусу противолежащего ей угла равно величине радиуса описанной окружности.
Теорема синусов может быть использована для решения различных геометрических задач. Например, с ее помощью можно найти длину стороны треугольника, если известны длины двух других сторон и величина угла между ними. Также теорема синусов позволяет найти значение синуса угла треугольника, зная длины его сторон.
Применение теоремы синусов не ограничивается только треугольниками. Она также может быть использована при работе с параллелограммами и трапециями, а также при нахождении высоты треугольника.
Таким образом, теорема синусов является важным инструментом в геометрии и находит широкое применение при решении задач, связанных с треугольниками и другими многоугольниками.
Расчет синуса по определению

Синус угла в геометрии можно вычислить по определению, используя формулу:
$$\sin\alpha = \frac{{AC}}{{AB}}$$
где:
- $$AB$$ - гипотенуза прямоугольного треугольника, где угол $$\alpha$$ является противолежащим;
- $$AC$$ - катет прямоугольного треугольника, лежащий против угла $$\alpha$$.
Для расчета синуса по определению необходимо знать длины сторон прямоугольного треугольника. Если эти данные имеются, можно приступить к вычислению синуса. Важно помнить, что значения синуса всегда лежат в диапазоне от -1 до 1.
График синусоиды и его особенности
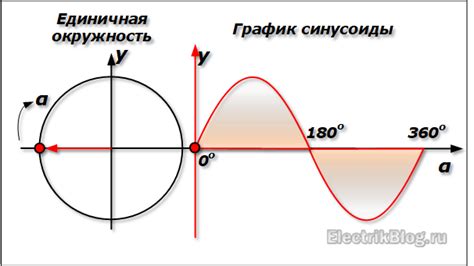
График синусоиды имеет несколько особенностей:
1. Периодичность: синусоида повторяется через определенные временные или пространственные интервалы. Так, для синусоиды, заданной функцией y = A * sin(Bx + C), период равен 2π/B.
2. Амплитуда: это максимальное значение, которое может принимать функция синуса. Амплитуда определяет вертикальный размер синусоиды и может быть изменена путем изменения значения A в уравнении.
3. Фаза: смещение синусоиды в горизонтальном направлении. Фаза определяется значением С в уравнении и позволяет перемещать или сдвигать синусоиду.
4. Пересечения с осями: синусоида пересекает ось y в точке (0, 0) и ось x в точках, кратных половине периода.
5. Симметрия: синусоида является нечетной функцией, что означает, что значения функции синуса для отрицательных значений аргумента симметричны значениям для положительных значений аргумента.
График синусоиды имеет широкий спектр применений, включая анализ колебаний, электрических сигналов, звуковых волн и многого другого. Понимание особенностей графика синусоиды поможет лучше понять свойства данной функции и применять ее в различных математических и физических задачах.
Связь с другими тригонометрическими функциями

Синус угла можно определить как отношение противолежащего катета к гипотенузе прямоугольного треугольника. Он обозначается как sin(угол).
Связь синуса с другими тригонометрическими функциями выражается следующим образом:
1. Косинус (cos) - это отношение прилежащего катета к гипотенузе прямоугольного треугольника. Используя определение синуса, мы можем выразить косинус как cos(угол) = sin(90° - угол).
2. Тангенс (tg) - это отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Он связан с синусом следующим образом: tg(угол) = sin(угол) / cos(угол).
3. Котангенс (ctg) - это обратное значение тангенса. Он связан с синусом следующим образом: ctg(угол) = 1 / tg(угол) = cos(угол) / sin(угол).
4. Секанс (sec) - это обратное значение косинуса. Он связан с синусом следующим образом: sec(угол) = 1 / cos(угол) = 1 / sin(90° - угол).
5. Косеканс (cosec) - это обратное значение синуса. Он связан с синусом следующим образом: cosec(угол) = 1 / sin(угол) = 1 / cos(90° - угол).
Таким образом, синус угла имеет тесную связь с другими тригонометрическими функциями, что делает его важным инструментом в решении геометрических задач и изучении связей между углами и сторонами треугольника.
Практические задачи на применение синуса

Задача 1: Найдите длину отрезка AC, если известно, что угол BAC равен 45 градусов, а длины отрезков AB и BC равны, соответственно, 5 см и 7 см. (подсказка: используйте теорему синусов)
Задача 2: В треугольнике ABC известны длины сторон AB, BC и угол BAC. Найдите длину стороны AC. (подсказка: используйте теорему синусов)
Задача 3: Отрезок AC является диаметром окружности, вписанной в треугольник ABC. Угол ACB равен 30 градусов. Найдите угол ABC. (подсказка: используйте теорему синусов)
Задача 4: В треугольнике ABC известны длины сторон AB и BC, а также угол BAC. Найдите площадь треугольника ABC. (подсказка: используйте теорему синусов)
Это лишь несколько примеров задач, в которых можно применять синус. Знание этой тригонометрической функции поможет вам решать разнообразные задачи, связанные с геометрией и измерением углов.



