Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны друг другу. Все углы параллелограмма прямые. Однако, интересно узнать, чему равна сумма противолежащих углов в этом геометрическом фигуре.
В параллелограмме противолежащие углы равны между собой. То есть, если мы обозначим соответствующими буквами эти углы, например, А и C, то их величина будет одинакова. Это свойство можно доказать, воспользовавшись геометрической теоремой о параллельных прямых, пересекающихся на пересекающих их прямых.
Таким образом, сумма противолежащих углов в параллелограмме равна 180 градусам. Это значит, что если мы знаем величину одного угла параллелограмма, мы можем вычислить величину всех остальных углов.
Понятие параллелограмма и его углы
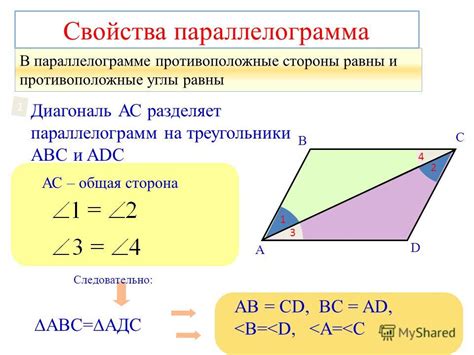
У параллелограмма есть несколько характеристик, включая углы:
- Угол между противоположными сторонами: Угол между противоположными сторонами параллелограмма всегда равен другому углу между параллельными сторонами. Таким образом, если один из углов параллелограмма равен 90 градусам, то все его углы будут прямыми.
- Угол на боковой стороне: Угол между боковой стороной параллелограмма и продолжением противоположной стороны также равен другому углу на боковой стороне параллелограмма. То есть, если угол между одной из боковых сторон и продолжением противоположной стороны равен 60 градусам, то все углы на боковых сторонах будут равны 60 градусам.
Таким образом, сумма противолежащих углов в параллелограмме всегда равна 180 градусам, так как все его углы попарно равны.
Определение параллелограмма
1. Противоположные стороны параллельны. Данное свойство означает, что прямые, содержащие противоположные стороны параллелограмма, никогда не пересекаются.
2. Противоположные стороны равны. Это означает, что длины противоположных сторон параллелограмма равны.
3. Противоположные углы равны. Углы, образованные пересечением диагоналей параллелограмма, равны между собой.
4. Сумма противолежащих углов равна 180 градусам. Это означает, что сумма двух углов, противолежащих друг другу в параллелограмме, равна 180 градусам.
Параллелограммы широко используются в геометрии и строительстве благодаря своим простым и понятным свойствам. Они являются основой для изучения других четырехугольников и многих других фигур.
Равные и противолежащие углы

Кроме того, сумма противолежащих углов в параллелограмме всегда равна 180 градусам. Таким образом, если один из углов параллелограмма равен 60 градусам, то противолежащий угол будет равен 120 градусам, их сумма будет составлять 180 градусов.
Равные и противолежащие углы в параллелограмме имеют важное значение при решении задач на построение и вычисление различных параметров фигуры.
Свойство суммы противолежащих углов
В параллелограмме сумма мер противолежащих углов всегда равна 180 градусам.
Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине. Одно из важных свойств параллелограмма - это равенство суммы мер противолежащих углов.
Сумма двух противолежащих углов в параллелограмме всегда равна 180 градусам. Например, если один угол параллелограмма равен 60 градусам, то противолежащий ему угол будет равен 180 градусам минус 60 градусов, то есть 120 градусам.
Это свойство может быть использовано для проверки параллельности сторон в фигурах. Если в четырехугольнике сумма мер противолежащих углов равна 180 градусам, то это говорит о том, что стороны этого четырехугольника параллельны.
Свойство суммы противолежащих углов в параллелограмме

Параллелограмм обладает двумя парами противолежащих углов, то есть углами, которые расположены напротив друг друга по парам. Если обозначить эти углы как A, B, C и D, то углы A и C будут противолежащими, а также углы B и D. Свойство этой фигуры гласит, что сумма углов A и C всегда равна сумме углов B и D, и эти суммы равны 180 градусов.
| Углы A и C (противолежащие) | Углы B и D (противолежащие) |
Это свойство можно доказать, используя различные геометрические теоремы и соотношения. Например, можно применить параллельные линии и их соответствующие углы, а также свойства треугольников.
Зная о таком свойстве параллелограмма, можно решать различные задачи, связанные с этой фигурой. Например, если известны значения двух противолежащих углов, можно найти значения двух других. Или наоборот, по заданным значениям двух углов можно установить, является ли данный четырехугольник параллелограммом.
Формула для нахождения суммы противолежащих углов

В параллелограмме сумма противолежащих углов всегда равна 180 градусам.
| Угол 1 | Угол 2 | Противолежащий угол |
|---|---|---|
| Угол A | Угол B | Угол B |
| Угол B | Угол C | Угол A |
| Угол C | Угол D | Угол D |
| Угол D | Угол A | Угол C |
Эта формула справедлива для любого параллелограмма, независимо от размеров его сторон и углов.
Найдя один противолежащий угол, можно сразу найти остальные, используя эту формулу.
Формула для нахождения суммы противолежащих углов в параллелограмме
В параллелограмме, противолежащие углы равны по величине, то есть они имеют одинаковую меру. Сумма таких углов в параллелограмме всегда равна 180 градусам.
Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине.
Данная формула может быть выражена следующим образом:
Сумма противолежащих углов = 180°
Это означает, что если у нас есть параллелограмм с углами А, В, С и D, то:
Угол А + Угол С = 180°
Угол В + Угол D = 180°
Таким образом, сумма противолежащих углов в параллелограмме всегда будет равна 180 градусам, не зависимо от размера или формы параллелограмма.



