Программирование - это не только создание кода и выполнение задач, но и наука, требующая понимания математических основ. Высшая математика играет ключевую роль в программировании, помогая программистам решать сложные задачи и создавать эффективные алгоритмы.
Одним из основных применений высшей математики в программировании является анализ данных. Знание математических методов и статистики позволяет программисту проводить комплексный анализ больших объемов данных, определять закономерности и прогнозировать результаты. Например, это может быть полезно в разработке алгоритмов машинного обучения.
Кроме того, высшая математика помогает программистам оптимизировать код и создавать эффективные алгоритмы. Знание алгебры, теории графов и аналитической геометрии позволяет разрабатывать алгоритмы с минимальным числом операций и использовать ресурсы компьютера более эффективно.
Понимание математических основ также позволяет программисту уверенно работать с различными фреймворками и библиотеками, которые используют математические концепции. Особенно это актуально в областях, связанных с компьютерной графикой, симуляцией физических процессов, криптографией и многими другими.
В итоге, высшая математика является неотъемлемой частью программирования. Она помогает программистам решать сложные задачи, оптимизировать код и разрабатывать эффективные алгоритмы. Поэтому, если вы хотите стать настоящим профессионалом в области программирования, необходимо углубиться в изучение высшей математики и применять ее знания на практике.
Польза высшей математики в программировании

Высшая математика имеет огромное значение в программировании. Ее понимание и применение помогает разработчикам создавать более эффективные алгоритмы, решать сложные задачи и улучшать качество программного кода.
Основные области высшей математики, которые активно применяются в программировании, включают:
- Анализ - изучает свойства функций, их изменения, скорости роста и подходит для определения наилучших стратегий решения задач.
- Линейная алгебра - используется для работы с векторами, матрицами и линейными преобразованиями, что позволяет эффективно решать задачи, связанные с графикой, машинным обучением и обработкой изображений.
- Теория вероятности и статистика - помогает разработчикам анализировать данные, предсказывать результаты и принимать решения на основе статистических моделей.
- Дискретная математика - область, изучающая объекты, которые имеют конечное количество элементов. Она активно применяется в теории графов, комбинаторике и алгоритмах, что помогает разработчикам эффективно обрабатывать данные и решать задачи, связанные с сетями и оптимизацией.
Понимание этих математических концепций позволяет программистам более глубоко проникнуть в суть проблемы и найти наиболее эффективное решение.
Также, высшая математика способствует развитию логического мышления, абстрактного и критического мышления, что является ключевым для успешного программирования. Она помогает программистам видеть связи, отображать их в коде и идентифицироватьскрытые шаблоны.
В целом, понимание высшей математики дает программистам преимущество, помогает им разрабатывать более устойчивое и эффективное программное обеспечение и быть более независимыми от сторонних модулей и библиотек.
Оптимизация алгоритмов и времени работы

Высшая математика в программировании играет важную роль при оптимизации алгоритмов и улучшении времени работы программы. Знания математических концепций позволяют разработчикам создавать эффективные алгоритмы, которые выполняются быстро и эффективно.
Математические методы, такие как анализ сложности алгоритмов, теория вероятностей и алгоритмы оптимизации, помогают программистам понять, какие алгоритмы и структуры данных лучше использовать для достижения максимальной эффективности программы.
Оптимизация алгоритмов включает в себя изменение или переписывание кода таким образом, чтобы алгоритм выполнялся быстрее или потреблял меньше ресурсов. Это может быть особенно полезно, когда необходимо обрабатывать большие объемы данных или выполнить сложные вычисления.
Понимание математических концепций позволяет программистам определить время выполнения алгоритма и производительность программы в целом. Это позволяет обнаружить возможные проблемы и улучшить код, чтобы достичь оптимальной производительности.
Кроме того, математические методы позволяют программистам предсказывать, какие данные или сценарии будут наиболее нагруженными для программы, и адаптировать алгоритмы и структуры данных, чтобы обеспечить приемлимую производительность в таких ситуациях.
- Анализ сложности алгоритмов помогает оценить время выполнения алгоритма относительно размера входных данных.
- Теория вероятностей помогает предсказать вероятность возникновения определенных случаев и использовать эту информацию для оптимизации алгоритмов.
- Алгоритмы оптимизации позволяют найти наилучший способ решения задачи, выбрав оптимальные значения параметров и настройки.
Использование высшей математики позволяет программистам создавать более эффективные программы, которые работают быстро и рационально используют ресурсы. Это особенно важно в современной информационной среде, в которой все больше данных обрабатывается и передается в режиме реального времени.
Работа с большими данными

В программировании неизбежно сталкиваются с передачей, хранением и обработкой больших объемов данных. Работа с такими данными требует применения специальных инструментов и подходов, а знания высшей математики могут значительно облегчить этот процесс.
Одним из ключевых аспектов работы с большими данными является их анализ и обработка. Здесь математические методы приходят на помощь, позволяя производить сложные вычисления и найти в данных интересующую информацию.
В частности, теория вероятностей и статистика позволяют оценить вероятность исходов, анализировать взаимосвязи между данными и определять степень зависимости между различными переменными. Линейная алгебра и матричные вычисления могут использоваться для работы с матричными данными, например, при обработке изображений или анализе графов.
Кроме того, высшая математика также имеет применение в задачах машинного обучения и искусственного интеллекта. Методы оптимизации, дифференциального и интегрального исчисления позволяют оптимизировать алгоритмы и находить оптимальные решения для поставленных задач.
Правильное применение математических методов и инструментов позволяет эффективно работать с большими данными, сократить время обработки и получить глубокий анализ информации. Поэтому знание высшей математики в программировании является неотъемлемой частью профессиональных навыков и может значительно повысить эффективность разработчика.
Стоит отметить, что не всегда нужно решать математические задачи «с нуля». Существует множество библиотек и фреймворков, которые предоставляют готовые реализации алгоритмов и методов для работы с большими данными. Однако понимание математических основ и принципов работы этих инструментов позволяет лучше использовать их возможности и адаптировать для своих конкретных задач.
Создание сложных моделей и алгоритмов

Высшая математика в программировании играет важнейшую роль при создании сложных моделей и алгоритмов. Она позволяет программистам анализировать и описывать сложные системы с помощью математических моделей и элементов теории графов.
С использованием алгебры и анализа можно понять, как взаимодействуют части сложной системы, провести анализ ее поведения в различных ситуациях и прогнозировать результаты. Это особенно важно при работе с большими объемами данных и при моделировании сложных процессов, таких как финансовые рынки, погода или биологические системы.
Кроме того, высшая математика помогает разработке эффективных алгоритмов решения задач. Дифференциальное и интегральное исчисление, теория вероятностей и линейная алгебра позволяют оптимизировать процессы и улучшить производительность программного обеспечения.
На практике, программисты применяют высшую математику для разработки алгоритмов машинного обучения, компьютерного зрения, обработки сигналов и других сложных систем. Математические методы позволяют создавать точные и надежные модели, которые могут быть использованы для решения сложных задач в реальном мире.
- Моделирование социальных сетей: Высшая математика позволяет анализировать связи между пользователями социальных сетей, предсказывать их поведение и разрабатывать алгоритмы рекомендаций.
- Оптимизация процессов: С помощью математических методов можно оптимизировать процессы в производстве и логистике, что позволит снизить затраты и повысить эффективность.
- Криптография: Высшая математика является важной составляющей при разработке алгоритмов шифрования и защиты информации.
Анализ и прогнозирование данных
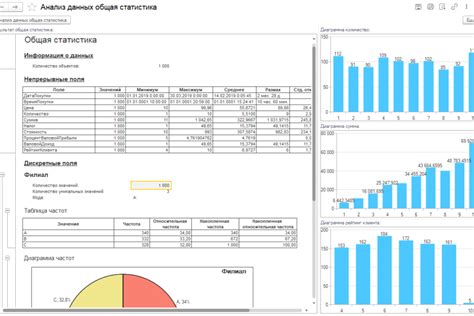
Высшая математика играет важную роль в анализе и прогнозировании данных в программировании. Она позволяет нам применять различные методы и алгоритмы для обработки и интерпретации больших объемов информации.
Один из основных инструментов анализа данных - статистика. При помощи статистических методов мы можем определить закономерности и зависимости в данных, а также оценить вероятности различных событий. Например, мы можем использовать статистические методы для анализа продаж в компании и прогнозирования их развития в будущем.
Математическое моделирование - еще один важный инструмент анализа и прогнозирования данных. Мы можем создавать математические модели, которые отражают особенности исследуемого процесса или явления. Затем, используя эти модели, мы можем предсказывать будущие значения исследуемых переменных. Например, математическое моделирование используется в экономике для прогнозирования цен на товары.
Машинное обучение - это еще одна область, где высшая математика необходима для анализа и прогнозирования данных. Мы можем использовать различные алгоритмы машинного обучения, такие как линейная регрессия, деревья решений или нейронные сети, для построения моделей, которые способны делать предсказания на основе имеющихся данных. Например, мы можем использовать машинное обучение для анализа данных о клиентах и прогнозирования их предпочтений или поведения.
Таким образом, высшая математика является неотъемлемой частью анализа и прогнозирования данных в программировании. Она предоставляет нам мощные инструменты и методы для работы с большими объемами информации и позволяет нам принимать обоснованные решения на основе данных.
| Примеры применения высшей математики в анализе и прогнозировании данных: |
|---|
| Анализ финансовых данных для прогнозирования движения рынка |
| Анализ клиентских данных для предсказания их предпочтений |
| Анализ медицинских данных для выявления закономерностей в заболеваниях |
Работа с функциями и графами
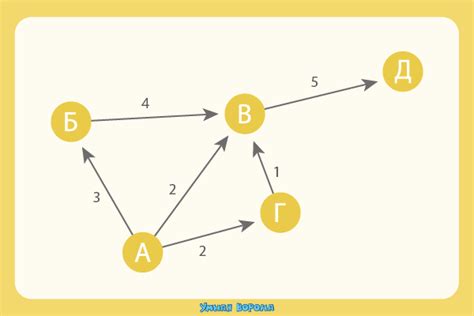
Работа с функциями в программировании включает в себя множество операций, таких как определение функции, вычисление значения функции, нахождение производной и интеграла, решение уравнений и неравенств, построение графиков и т.д. Знание математических концепций и методов позволяет более эффективно и точно работать с функциями.
Графы являются другим важным инструментом, используемым при программировании. Они позволяют представлять и анализировать сложные структуры данных, моделировать сети и взаимодействия между объектами. Работа с графами включает в себя такие операции, как поиск кратчайшего пути, обходы графа, определение связности и цикличности, анализ сетевых структур и т.д.
Понимание математических концепций и методов, связанных с функциями и графами, позволяет нам решать сложные задачи в программировании более эффективно. Оно помогает нам строить более точные модели и разрабатывать алгоритмы, основанные на математическом анализе данных. Поэтому знание высшей математики является неотъемлемой частью профессионального программирования.
Разработка криптографических алгоритмов
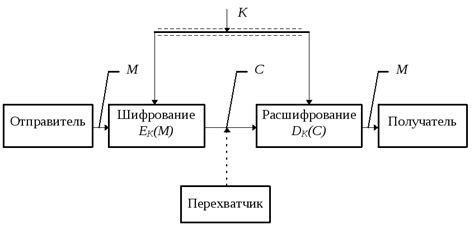
Высшая математика играет ключевую роль в разработке криптографических алгоритмов, которые используются для защиты информации в сети. Криптографические алгоритмы основаны на сложных математических принципах, и их безопасность зависит от математических основ.
Одним из важных аспектов при разработке криптографических алгоритмов является математическая теория чисел, которая изучает свойства чисел и их взаимоотношения. Одной из основных областей математической теории чисел, которая используется в криптографии, является теория модульных функций.
Теория модульных функций включает в себя такие понятия, как простые числа, модульная арифметика, китайская теорема об остатках и дискретное логарифмирование. Она позволяет разработчикам создавать криптоматематические алгоритмы, которые обладают свойствами неразрывности и непреодолимости для злоумышленников.
Кроме того, разработка криптографических алгоритмов также требует знания теории вероятностей и теории информации. Теория вероятностей позволяет оценивать степень надежности и безопасности алгоритмов. Теория информации, в свою очередь, помогает определить эффективность алгоритмов и максимально использовать доступный объем информации.
Важно отметить, что разработка криптографических алгоритмов требует глубокого понимания математических основ и умения применять их на практике. Для программиста, работающего с криптографическими алгоритмами, владение высшей математикой является необходимым условием для успешной работы и обеспечения информационной безопасности.
Проектирование и оптимизация баз данных

Проектирование баз данных включает в себя создание структуры данных, определение отношений между таблицами и выбор подходящих типов данных для хранения информации. Здесь математические знания могут быть полезными при определении ключей, атрибутов и ограничений, а также при оптимизации запросов к базе данных.
Высшая математика может помочь в разработке математических моделей, которые используются для анализа данных и принятия решений. Такие модели могут быть основаны на теории вероятности, линейной алгебре или теории графов, например.
При оптимизации баз данных математические методы позволяют улучшить производительность системы, минимизировать затраты и сократить время выполнения запросов. Алгоритмы оптимизации и статистические методы играют важную роль в этом процессе, позволяя эффективно использовать ресурсы и улучшить производительность баз данных.
Таким образом, знание высшей математики является необходимым инструментом для проектирования и оптимизации баз данных, позволяя разработчикам создавать эффективные и надежные системы хранения и обработки информации.
Разработка игр и графических приложений

Высшая математика играет важную роль в разработке игр и графических приложений, предоставляя программистам необходимые инструменты для создания реалистичных и интерактивных миров.
Одним из основных аспектов, где математика непосредственно применяется, является работа с трехмерной графикой. Благодаря математическим моделям и алгоритмам компьютерной графики, разработчики могут создавать трехмерные объекты, текстуры, освещение и эффекты, которые делают игровой мир более реалистичным.
Другой важной областью математики в разработке игр является физика. Математические методы и модели позволяют смоделировать взаимодействие объектов в игровом мире, например, силы гравитации, коллизии и движение. Благодаря этому, игроки могут наслаждаться более реальными физическими эффектами и поведением объектов.
Отличное знание математики позволяет программистам создавать сложные алгоритмы и структуры данных, необходимые для обработки больших объемов информации, расчетов и оптимизации производительности игр и графических приложений.
Кроме того, понимание математических концепций, таких как векторы, матрицы, алгоритмы оптимизации и статистика, помогает программистам разрабатывать эффективные алгоритмы и архитектуру игровых движков, управление камерой, анимацию персонажей и многое другое.
Таким образом, высшая математика является неотъемлемой частью разработки игр и графических приложений, обеспечивая программистам необходимые инструменты и знания для создания захватывающих и уникальных визуальных и игровых эффектов.
Реализация и работа с искусственным интеллектом

Высшая математика играет ключевую роль в решении таких задач, как классификация данных, анализ изображений и текстов, обработка естественного языка и другие. Алгоритмы машинного обучения и нейронные сети, на которых основаны многие системы искусственного интеллекта, строятся на математических моделях, таких как линейная алгебра, теория графов и математическая оптимизация.
Одним из наиболее популярных подходов к решению задач искусственного интеллекта является глубокое обучение (deep learning). Оно базируется на нейронных сетях с большим количеством слоев и нелинейных функций активации. Для эффективной работы с такими сетями необходимо обладать знаниями в области математического анализа, теории вероятностей, численных методов и оптимизации.
Работа с искусственным интеллектом также требует умения анализировать и интерпретировать результаты, полученные моделями машинного обучения. Для этого необходимы знания в области статистики, теории вероятностей и экспериментального анализа данных. Аналитические методы, такие как регрессия, классификация и кластеризация, часто используются для извлечения информации из больших объемов данных и принятия решений на основе полученных результатов.
В целом, понимание и применение высшей математики в программировании является необходимым условием для успешной реализации и работы с искусственным интеллектом. Без этого знания, разработка сложных алгоритмов, обработка данных и принятие решений на основе их анализа становятся гораздо сложнее и менее эффективными.
| Область искусственного интеллекта | Необходимая математика |
|---|---|
| Машинное обучение | Линейная алгебра, теория вероятностей, оптимизация |
| Глубокое обучение | Математический анализ, теория вероятностей, численные методы, оптимизация |
| Анализ данных | Статистика, теория вероятностей, экспериментальный анализ данных |
Роль высшей математики в машинном обучении
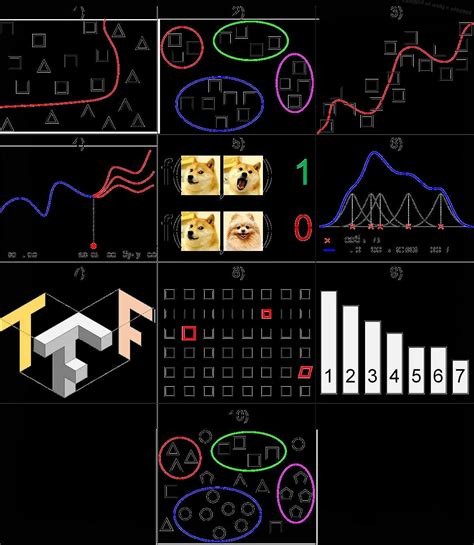
Математика является языком машинного обучения, который позволяет выразить и формализовать различные задачи и концепции. Без понимания математических моделей и алгоритмов, использование машинного обучения становится сложным, если не невозможным. Именно математические методы позволяют обучающей системе "понять" данные, искать в них закономерности и создавать прогнозы.
Одной из основных областей математики, применяемой в машинном обучении, является статистика. Статистические методы помогают анализировать данные, определять связи между переменными, строить модели и проверять их на достоверность. Без статистики невозможно провести корректные и точные оценки и предсказания.
Также в машинном обучении широко применяется линейная алгебра. Линейная алгебра используется для работы с матрицами, векторами и системами линейных уравнений. Модели машинного обучения часто представляются в виде матриц и векторов, и алгебраические операции над ними позволяют эффективно решать задачи.
Другие ветви математики, которые тесно связаны с машинным обучением, включают теорию вероятности, дифференциальное исчисление и оптимизацию. Теория вероятности помогает моделировать случайные процессы и оценивать вероятности событий. Дифференциальное исчисление используется для оценки функций и поиска их экстремумов. Оптимизация помогает находить оптимальные параметры моделей и алгоритмов.
Таким образом, высшая математика является неотъемлемой частью машинного обучения. Она обеспечивает необходимые теоретические основы и инструменты для разработки и применения алгоритмов и моделей. Понимание и применение математических концепций позволяет эффективно использовать машинное обучение для решения различных задач во многих областях.



