Математика пронизывает нашу жизнь, она везде: в повседневных наблюдениях, в технологических процессах и даже в нашем мозге. Одной из основных операций в математике является сложение. Мы все знаем, как сложить два числа, но сегодня мы рассмотрим эту операцию более подробно и узнаем, как правильно выполнить сложение чисел любой сложности.
Сложение чисел – это элементарная математическая операция, которая заключается в объединении двух или более чисел для получения их суммы. Легко представить, как сложить два числа на бумаге или в уме, но иногда мы сталкиваемся со сложными числовыми выражениями, требующими более тщательной работы.
Прежде чем говорить о сложении чисел, важно отметить, что числа могут быть положительными, отрицательными и нулевыми. Положительные числа представляют собой значения, большие нуля, отрицательные числа – значения, меньшие нуля, а нулевые числа – само значение нуля. Учитывая эти особенности, мы можем приступить к сложению чисел и их суммированию.
Числа и их сумма
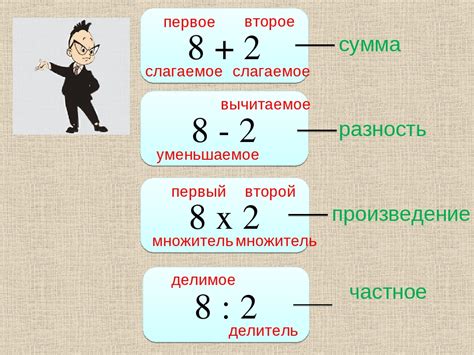
Сложение - одна из основных арифметических операций, которая выполняется над числами. Она позволяет находить сумму двух или более чисел. Для сложения используется специальный знак "+". Например, сумма чисел 2 и 3 равна 5 (2 + 3 = 5).
Хорошая практика при сложении чисел - начинать с меньшего числа и постепенно добавлять большие числа. Например, чтобы сложить числа 4 и 7, можно сначала прибавить 4 к 7, получив 11, а затем вычислить сумму чисел 4 и 11, равную 15.
Чтобы сложить числа, следует придерживаться определенных правил. Например, когда складываются числа разных знаков, результирующая сумма будет иметь знак числа с большим модулем. Если оба числа положительные, результат будет положительным. Если оба числа отрицательные, результат будет отрицательным.
Сложение чисел можно представить в виде таблицы. Ниже приведен пример таблицы сложения двух чисел:
| Первое число | Второе число | Сумма |
|---|---|---|
| 4 | 7 | 11 |
| -2 | 5 | 3 |
| 8 | -6 | 2 |
Понятие числа

Цифры - это символы, которые используются для записи чисел. Они представляют различные значения в зависимости от их позиции в числе.
Числа могут быть классифицированы на различные типы в зависимости от их свойств. Например, числа могут быть натуральными, целыми, рациональными, иррациональными или комплексными.
Когда мы складываем два числа, мы комбинируем их значения, чтобы получить общую сумму. Правильное сложение чисел может быть выполнено с использованием алгоритма, который базируется на понимании их структуры и свойств.
Как сложить два числа

- Возьмите первое число, которое вы хотите сложить, и запишите его.
- Возьмите второе число, которое вы хотите сложить, и запишите его под первым числом.
- Выровняйте числа по позициям цифр, чтобы цифры единиц находились одна под другой, десятки - под десятками, и так далее.
- Начиная с последних цифр (цифры единиц), сложите их вместе.
- Если сумма превышает 9, перенесите "единицу" (десятка) к следующей позиции (десятки).
- Продолжайте сложение, переходя от меньших разрядов к большим, пока не закончатся все цифры.
Результат сложения будет являться суммой двух чисел. Запишите его под вторым числом.
Сумма двух чисел может быть использована для решения различных задач, арифметических вычислений и т.д.
Методы сложения чисел

Существует несколько методов сложения чисел, которые могут быть использованы в различных ситуациях:
1. Сложение в столбик
Этот метод позволяет сложить числа, записанные в столбик, по разрядам. Сначала складываются единицы, затем десятки и так далее. Этот метод основан на правиле сложения одноразрядных чисел и эффективен при работе с большими числами.
2. Сложение с использованием алгоритма
Для сложения чисел можно использовать алгоритм, основанный на правиле сложения двух чисел столбиком. Сначала складываются числа столбиком, затем происходит дополнительная обработка разрядов, если сумма превышает 9. Этот метод часто используется при программировании и автоматическом вычислении сумм.
3. Сложение по модулю
При сложении чисел по модулю результат получается отниманием единицы от суммы, если она превышает модуль числа. Например, при сложении 7 и 8 по модулю 10, получается результат 5. Этот метод широко используется в криптографии и математике.
Выбор метода сложения зависит от конкретной задачи и предпочтений исполнителя. Важно выбрать метод, который позволяет получить точный и корректный результат.
Сложение целых чисел

Если сумма в столбце меньше 10, то результат просто записывается в соответствующий разряд суммы. Если сумма больше или равна 10, то из нее берется только последняя цифра и результат сразу записывается в соответствующий разряд. Первая цифра из суммы называется «единицей переноса», которая передается в следующий столбец.
Если после сложения остается единица переноса, ее нужно записать в следующий разряд слева.
Например, чтобы сложить числа 47 и 25, нужно записать их в столбик:
47
+25
––
72
Здесь сначала сложили единицы (7+5=12), записали 2, а 1 запомнили к сумме десятков. Затем сложили десятки (4+2+1=7) и получили сумму 72.
Таким образом, сложение целых чисел – это простая и понятная операция, которую можно выполнить, используя столбиковый метод.
Сложение дробных чисел

Для сложения дробных чисел необходимо выполнить следующие шаги:
- Убедитесь, что знаменатели дробей одинаковы. Если знаменатели разные, переведите дроби в общий знаменатель. Для этого найдите наименьшее общее кратное (НОК) знаменателей и приведите оба числа к новому знаменателю, не забывая изменить и числители соответственно.
- Сложите числители дробей и сохраните знаменатель без изменений.
- Упростите полученную дробь, если это возможно. Для этого найдите наибольший общий делитель (НОД) числителя и знаменателя и разделите оба значения на этот НОД.
- Результатом сложения дробных чисел будет новая дробь с полученным числителем и сохраненным знаменателем.
Например, для сложения дробей 2/5 и 3/5 необходимо привести оба числа к общему знаменателю, который равен 5. Таким образом, получаем дроби 2/5 и 3/5. Затем, сложив их числители, получаем 5/5, что равно 1. Новая дробь имеет числитель 1 и знаменатель 5.
Сложение дробных чисел требует внимательности и точности, поэтому рекомендуется выполнять все шаги методично и проверять результаты на корректность. Теперь, когда вы знаете основы сложения дробей, можно приступить к более сложным операциям с дробными числами.
Сложение отрицательных чисел

Сложение отрицательных чисел представляет собой операцию, в которой требуется сложить два или более числа, каждое из которых имеет отрицательное значение. Правильное сложение отрицательных чисел основывается на правилах арифметики и требует обратить особое внимание на знак каждого числа.
Если у нас есть два отрицательных числа, их сумма будет также отрицательным числом. При сложении отрицательных чисел нужно сложить модули чисел (т.е. их абсолютные значения) и приписать к результату знак минус.
Например, если у нас есть числа -3 и -5, мы сначала складываем их модули: 3 + 5 = 8, а затем приписываем знак минус: -8. Итак, -3 + -5 = -8.
Но что делать, если одно число положительное, а другое отрицательное? В этом случае мы вычитаем модуль отрицательного числа из модуля положительного числа и результату приписываем знак числа с большим модулем.
Например, если у нас есть числа -7 и 4, мы сначала вычитаем модуль отрицательного числа из модуля положительного числа: 7 - 4 = 3. Поскольку отрицательное число имеет больший модуль, мы приписываем знак минус: -3. Итак, -7 + 4 = -3.
Таким образом, для правильного сложения отрицательных чисел необходимо учитывать их знаки и модули и следовать правилам арифметики для получения верного результата.
Сложение с помощью десятичной системы

Сложение в десятичной системе осуществляется следующим образом:
- Ставим слагаемые одно под другим так, чтобы разряды совпадали.
- Складываем цифры в одном разряде. Если сумма больше или равна 10, то оставляем единицы и записываем десятки в следующий разряд.
- Продолжаем сложение, переходя к следующим разрядам, пока все разряды не будут просуммированы.
Пример:
- 23
- + 48
- ------
- 71
В этом примере мы сложили два числа, 23 и 48, записанные в десятичной системе. Первая цифра в сложении - 3 + 8 - дает нам 11. Мы записываем 1 и переносим 10 в следующий разряд. Затем складываем 2 и 4 и добавляем перенос 1, получая 7. Таким образом, сумма этих двух чисел равна 71.
Сложение с помощью десятичной системы - базовый навык, который необходимо знать для работы с числами. Это поможет нам в повседневной жизни, а также в более сложных математических операциях.
Округление суммы чисел

При округлении суммы чисел, следует учитывать правила округления, которые могут определяться требованиями конкретной задачи или стандартами округления. Например, в некоторых случаях округление производится до ближайшего целого числа, в других - до определенного количества десятичных знаков.
Для округления суммы чисел в программировании, часто применяются математические функции округления, такие как round(), ceil() или floor(). Эти функции позволяют округлить число с заданной точностью в соответствии с определенными правилами округления.
| Округление | Описание |
|---|---|
| Положительное округление | Округление вверх до ближайшего целого числа (например, 3.6 округляется до 4) |
| Отрицательное округление | Округление вниз до ближайшего целого числа (например, 3.6 округляется до 3) |
| Нулевое округление | Округление до ближайшего целого числа, в случае равенства остатка к половине шага (например, 3.5 округляется до 4, а 3.4 округляется до 3) |
Выбор метода округления зависит от требований задачи и конкретных условий. Важно учитывать, что округление суммы чисел может привести к искажению и потере точности данных, поэтому необходимо внимательно выбирать способ округления в каждом конкретном случае.
Проверка правильности суммирования
После выполнения сложения двух чисел имеет смысл проверить правильность полученного результата. Для этого можно использовать несколько методов:
- Проверка вручную. Для этого нужно взять каждое число отдельно и сложить их, записывая результаты. Затем сравнить полученную сумму с исходным результатом сложения. Если они совпадают, значит, суммирование выполнено правильно.
- Использование калькулятора. Многие калькуляторы имеют функцию сложения, которую можно использовать для проверки суммы двух чисел. Вводите числа по очереди, сложите их, а затем сравните результат с исходным значением. Если они равны, значит, суммирование прошло верно.
Независимо от выбранного метода, проверка правильности суммирования является важным шагом при работе с числами. Это позволяет убедиться в точности результата и избежать ошибок при дальнейшей обработке данных.



