Корень из отношения двух чисел – мощный инструмент, который позволяет нам определить, насколько одно число больше или меньше другого. Благодаря корню из отношения, мы можем выявить пропорциональность между числами, а также решить множество задач из разных областей науки и техники.
Основной формулой для вычисления корня из отношения двух чисел является r = √a/b, где r – корень, а a и b – числа, которые мы сравниваем. Кроме того, существуют различные способы вычисления корня из отношения, включая использование калькулятора, таблицы значений и графика функции.
Для вычисления корня из отношения с помощью калькулятора, необходимо найти специальную функцию, обозначаемую как "√" или "sqrt". После ввода чисел a и b, нужно применить эту функцию к выражению a/b, и результатом будет искомый корень из отношения.
Альтернативным способом вычисления корня из отношения является построение графика функции y = √x и использование таблицы значений, чтобы найти точку пересечения графика с осью x. При этом значение точки пересечения будет представлять собой корень из отношения a/b.
Извлечение корня из чисел: основная идея

Основная идея извлечения корня сводится к нахождению числа, при возведении которого в заданную степень получается исходное число. Например, корень квадратный из числа 16 равен 4, так как 4^2 = 16.
Формула для извлечения корня из числа следующая:
| Вид корня | Формула |
|---|---|
| Квадратный корень | √x = y, где y^2 = x |
| Кубический корень | ∛x = y, где y^3 = x |
| Четвертный корень | ∜x = y, где y^4 = x |
| И так далее... |
Способы вычисления корня могут быть различными, в зависимости от требуемой точности и доступных вычислительных ресурсов. Некоторые из самых популярных методов включают в себя метод Ньютона и метод двоичного поиска.
Важно заметить, что извлечение корня из числа может быть сложной задачей, особенно при работе с большими числами или нецелыми степенями. Поэтому для точных и эффективных вычислений рекомендуется использовать специальные математические библиотеки или встроенные функции в языках программирования.
Простой способ вычисления корня

Вычисление корня из отношения двух чисел может быть достаточно сложной задачей, но существуют и простые способы его решения. Один из таких способов основан на использовании метода приближенных значений.
Для вычисления корня из отношения двух чисел a и b можно воспользоваться следующей формулой:
корень из a/b = корень квадратный из a / корень квадратный из b
Эта формула позволяет разделить вычисление корня на две независимые операции: вычисление корня из числа a и вычисление корня из числа b.
Простым способом вычисления корня из числа можно воспользоваться, например, методом Ньютона. Он заключается в нескольких итерациях, на каждой из которых приближается значение корня. Это позволяет достичь большой точности исходного вычисления.
Следующий алгоритм может быть использован для таких вычислений:
- Установить начальное приближение корня (например, среднее арифметическое a и b).
- Повторять до достижения необходимой точности:
- Вычислить новое приближение корня, применяя формулу: новое_значение = (старое_значение + a/старое_значение) / 2.
- Вернуть полученное значение корня.
Таким образом, использование простого способа вычисления корня из отношения двух чисел позволяет упростить задачу и достичь точных результатов.
Идеальный квадрат и вычисление корня
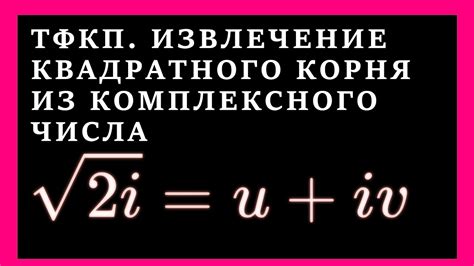
Вычисление корня из числа можно выполнить с помощью различных методов, включая простой математический алгоритм и использование калькулятора или компьютерной программы.
Простым математическим алгоритмом вычисления корня является метод Ньютона-Рафсона, который позволяет приближенно определить значение корня. Для этого нужно выбрать начальное приближение и повторять итеративный процесс до достижения необходимой точности.
Если вам нужно вычислить корень из числа на практике, вы можете воспользоваться калькулятором или специальными программами для работы с числами. В большинстве случаев это гораздо более удобный и быстрый способ, особенно при работе с большими числами.
Идеальные квадраты являются особенными числами, так как они имеют точные квадратные корни. Например, числа 1, 4, 9, 16, 25 и так далее являются идеальными квадратами, и их квадратные корни равны 1, 2, 3, 4, 5 и так далее.
Знание и понимание корня из чисел и идеальных квадратов полезно для решения различных задач и применения в математике, физике, программировании и других областях.
Численные методы нахождения корня
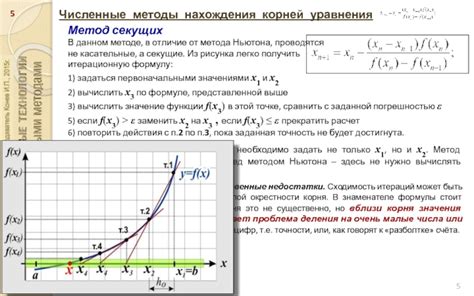
Найти корень из числа может быть достаточно сложно, особенно если речь идет о больших числах или нецелых числах. В таких случаях эффективными могут быть численные методы нахождения корня.
Одним из наиболее популярных численных методов является метод Ньютона. Он основан на итеративном приближении к корню путем использования касательной к графику функции в точке и нахождения пересечения этой касательной с осью абсцисс.
Другой распространенный метод - метод деления отрезка пополам. Он заключается в том, чтобы разделить отрезок, на котором находится корень, на две равные части и найти ту половину, в которой функция меняет знак. Затем процесс повторяется с этой половиной.
Еще один метод - метод простой итерации. Он заключается в замене исходного уравнения эквивалентным уравнением, корень которого легко найти, и последующей итерации до достижения нужной точности.
Также существуют и другие численные методы, такие как метод секущих, метод пристрелки и др. Каждый из них имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи.
Важно помнить, что численные методы нахождения корня могут давать приблизительное значение, а не точное. Поэтому при использовании таких методов необходимо учитывать их особенности и ограничения.
Алгоритм Ньютона-Рафсона

Алгоритм Ньютона-Рафсона использует локальное приближение к корню и последовательно его уточняет, пока не будет достигнута требуемая точность. Он начинается с некоторого начального приближения x0 и использует формулу:
xn+1 = xn - f(xn)/f'(xn)
Здесь xn - текущее приближение к корню, f(xn) - значение функции в точке xn, а f'(xn) - производная функции в точке xn.
Алгоритм Ньютона-Рафсона выполняется до тех пор, пока разность между текущим и предыдущим приближением не станет меньше определенного эпсилон (заданной точности).
Этот алгоритм является одним из самых эффективных методов нахождения корня из отношения двух чисел, особенно если уравнение имеет достаточно гладкую функцию и устойчивый корень.
Приближенное вычисление корня

Один из таких методов - метод Ньютона (или метод касательных). Он основан на замене задачи нахождения корня на задачу нахождения нуля функции. Для того чтобы применить данный метод, необходимо задать функцию, корнем которой будет искомое число. Затем выбирается начальное приближение к корню, итерационно вычисляются следующие приближения с помощью формулы:
Xn+1 = Xn - f(Xn)/f'(Xn)
где Xn+1 - приближение к корню на следующей итерации,
Xn - текущее приближение к корню,
f(Xn) - значение функции в точке Xn,
f'(Xn) - значение производной функции в точке Xn.
Метод Ньютона обладает квадратичной скоростью сходимости и позволяет достичь высокой точности вычисления корня. Однако для его применения необходимо уметь вычислять значение функции и её производной в заданной точке.
Кроме метода Ньютона, существуют и другие приближенные методы вычисления корня, такие как метод деления отрезка пополам, метод простой итерации и метод релаксации. Каждый из них имеет свои особенности и применяется в различных ситуациях.
Использование приближенных методов вычисления корня позволяет получить более точные результаты, особенно при работе с числами, не имеющими точного рационального корня. Однако приближенные вычисления могут быть более ресурсоемкими и требовать больше времени на выполнение, поэтому выбор метода вычисления корня должен быть основан на конкретных условиях и требованиях задачи.
Применение корня в математике и других областях

- Алгебра: Корень часто используется при решении уравнений. Для нахождения корней квадратного уравнения необходимо извлечь из дискриминанта корень. В общем случае, при решении уравнений различных степеней, корень может быть использован для нахождения одного или нескольких решений.
- Геометрия: Корень применяется для нахождения длин сторон различных геометрических фигур. Известная формула для нахождения длины гипотенузы прямоугольного треугольника, известные длины катетов – это также применение корня.
- Физика: Корень используется в многих формулах физических законов. Например, в формуле для вычисления скорости тела или для определения ускорения свободного падения.
- Финансы: Корень может применяться при расчете финансовых показателей, таких как доходность инвестиций, степень риска и прочее. Например, для определения средней годовой доходности инвестиций, необходимо извлечь корень из совокупной доходности за несколько лет.
Это лишь небольшой перечень областей, где применение корня является необходимым. В реальной жизни корень используется в самых различных задачах и позволяет получить точные решения и результаты.



