В алгебре, нашей важной задачей является нахождение значений выражений. Иногда выражения могут быть сложными и содержать переменные. Один из способов решить такие выражения - подставить значения переменных и вычислить результат. В данном случае нам дано выражение 4x2y3. Как нам найти его значение?
Для этого нам нужно знать значения переменных x и y. Значение x обозначает число, а значение y - тоже число. Подставим эти значения в наше выражение и произведем вычисление.
Например, если x=2 и y=3, мы можем вычислить 4x2y3. Подставим значения: 4*22*33. Посчитаем: 4*4*27=432.
Таким образом, когда x=2 и y=3, значение выражения 4x2y3 равно 432.
Что такое 4x^2y^3?
Разложив данное выражение на множители, получим:
- 4 - коэффициент
- x^2 - переменная x, возведенная в степень 2
- y^3 - переменная y, возведенная в степень 3
Значение 4x^2y^3 будет зависеть от значений переменных x и y. Подставив конкретные значения, можно вычислить результат данного выражения.
Определение и значение выражения

Значение этого выражения зависит от значений переменных x и y. Если известны числовые значения переменных, можно выполнить вычисления для получения конкретного числового значения выражения.
Выражение 4x^2y^3 используется в алгебре и математическом анализе для описания процессов, в которых присутствуют переменные и их степени. Оно может быть полезным при решении задач, связанных с множественными переменными и степенями.
Где и как использовать 4x^2y^3?
Одно из применений этого выражения - это в задачах на алгебру и арифметику. Его можно использовать для упрощения и решения уравнений, нахождения значений функций и выполнения других алгебраических операций.
В научных и инженерных расчетах 4x^2y^3 может представлять значимые физические величины, такие как объемы, массы, энергия и другие параметры.
Это выражение также может использоваться в контексте геометрии и тригонометрии для вычисления площадей, объемов, углов и других геометрических параметров.
Кроме того, 4x^2y^3 может быть использовано в программировании и компьютерной науке для определения значений переменных и вычисления результатов математических операций.
В целом, 4x^2y^3 является полезным выражением в алгебре и математике, которое может быть применено в различных областях знаний и практических задачах.
Примеры приложений в реальной жизни

Математическое выражение 4x^2y^3 имеет широкое применение в науке, технике и других сферах жизни. Ниже приведены несколько примеров его применения:
| Пример | Область применения |
|---|---|
| 1. | Физика |
| 2. | Электротехника |
| 3. | Экономика |
| 4. | Социология |
| 5. | Биология |
В физике, выражение 4x^2y^3 может использоваться для расчета различных физических величин, таких как сила, энергия или плотность. В электротехнике, оно может быть использовано для анализа и моделирования электрических цепей. В экономике, оно может быть применено для моделирования экономических процессов. В социологии, оно может использоваться для анализа социальных групп и взаимодействий. В биологии, оно может быть использовано для анализа генетической информации и моделирования различных биологических процессов.
Все эти примеры демонстрируют важность и широкое применение выражения 4x^2y^3 в реальной жизни. Оно позволяет выполнять различные вычисления и анализировать различные физические и социальные явления, что является неотъемлемой частью научного и технического прогресса.
Как найти значение 4x^2y^3?

Для того чтобы найти значение выражения 4x^2y^3, нужно подставить конкретные значения переменных x и y вместо их символических обозначений и выполнить необходимые арифметические операции.
Коэффициент перед переменными в данном случае равен 4, степень переменной x равна 2, а степень переменной y равна 3. Поэтому общее значение выражения можно найти следующим образом:
1. Возьмем, например, x = 3 и y = 2.
2. Подставим значения переменных в выражение: 4 * (3)^2 * (2)^3 = 4 * 9 * 8 = 288.
Таким образом, при данных значениях переменных x и y, значение выражения 4x^2y^3 равно 288.
Использование правил алгебры для расчета

Для примера, рассмотрим выражение 4x^2y^3. В этом выражении есть две переменные - x и y, возведенные в степени 2 и 3 соответственно. Чтобы вычислить значение этого выражения, нужно перемножить коэффициент 4 на переменные x и y, возведенные в соответствующие степени.
По правилу умножения многочлена на многочлен, необходимо перемножить все члены первого многочлена на все члены второго многочлена. В данном случае у нас есть один член в первом многочлене (4x^2y^3) и один член во втором многочлене (1).
| Первый многочлен | Второй многочлен | Результат |
|---|---|---|
| 4x^2y^3 | 1 | 4x^2y^3 |
Таким образом, значение выражения 4x^2y^3 будет равно 4x^2y^3.
Это простой пример использования правил алгебры для расчета значения многочлена. В более сложных случаях можно применять несколько правил одновременно, чтобы получить более сложные выражения.
Какие факторы влияют на значение 4x^2y^3?

Значение выражения 4x^2y^3 зависит от нескольких факторов:
| Фактор | Влияние |
|---|---|
| x | Значение переменной x определяет величину внутри выражения. Если значение x равно нулю, то весь член 4x^2y^3 обратится в ноль. |
| y | Значение переменной y также влияет на результат выражения. Если значение y равно нулю, то весь член 4x^2y^3 обратится в ноль. Если значение y отрицательное, то результат будет отрицательным. |
Таким образом, значения переменных x и y влияют на итоговую величину выражения 4x^2y^3. Учитывая значения этих переменных, можно вычислить точное значение выражения.
Роль переменных x и y в выражении
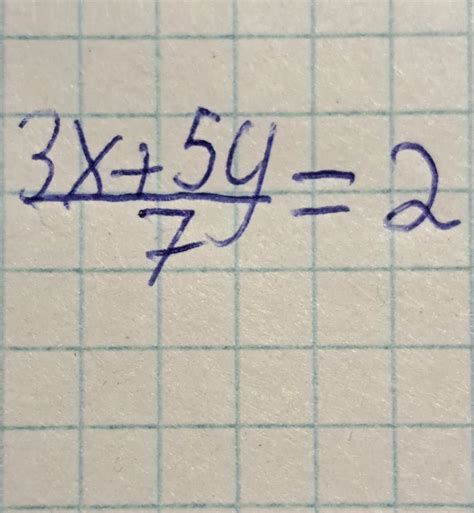
Переменная x, возведенная в степень 2, указывает, что значение переменной умножается на саму себя. А переменная y, возведенная в степень 3, указывает, что значение переменной умножается на саму себя дважды. Коэффициент 4 перед выражением увеличивает значение, полученное из произведения переменных x^2y^3 в 4 раза.
Таким образом, переменные x и y в выражении 4x^2y^3 определяют величину и изменчивость этого алгебраического выражения, и их значения могут значительно влиять на результат вычислений.
Какие ошибки могут возникнуть при вычислении 4x^2y^3?
При вычислении выражения 4x^2y^3 могут возникнуть следующие ошибки:
Ошибки в подстановке значений переменных. Если в выражении используются переменные x и y, необходимо правильно подставить их значения перед вычислением. В случае неправильной подстановки значений, результат вычисления будет неверным.
Ошибки в возведении в степень. Возведение переменных x и y в степень может вызвать ошибки, если не правильно указана степень. Например, при неправильном указании степени выражения x^2 или y^3, результат вычисления будет неверным.
Ошибки в умножении и перемножении переменных. При умножении переменных x и y могут возникнуть ошибки при неправильном умножении или перемножении. Например, если забыть умножить коэффициент 4 на переменные x^2 и y^3, результат вычисления будет неверным.
Для получения правильного результата при вычислении 4x^2y^3 необходимо правильно подставить значения переменных, указать степени правильно и произвести правильное умножение и перемножение переменных.
Частые путаницы и заблуждения

Математика как наука зачастую становится источником путаницы и заблуждений для многих людей. В частности, в алгебре, при работе с переменными и выражениями, многие сталкиваются с трудностями и ошибками.
Одна из частых ошибок связана с путаницей в понимании и использовании символов и операций. Например, выражение "4x^2y^3" может вызвать замешательство и непонимание. Ошибочно считается, что x^2 означает умножение x на 2, аналогично с y^3. Однако, в алгебре символ "^" обозначает возведение в степень, а не умножение.
Таким образом, выражение "4x^2y^3" означает, что переменные x и y возводятся в степени 2 и 3 соответственно, а затем перемножаются с коэффициентом 4.
| Выражение | Значение |
|---|---|
| 4x^2y^3 | 4 * (x^2) * (y^3) |
Путаница и неправильное понимание таких выражений может привести к серьезным ошибкам в математических вычислениях и решении уравнений. Поэтому важно помнить о правильном понимании символов и операций в алгебре и быть внимательным при работе с ними.



