Угол в правильной четырехугольной пирамиде - это угол между любой стороной основания и высотой пирамиды, проведенной из вершины в центр основания. В правильной четырехугольной пирамиде все стороны основания равны, а все углы между сторонами основания и высотой равны. Такая пирамида имеет четыре основания, состоящих из равных сторон.
Уравнение угла в правильной четырехугольной пирамиде можно выразить следующим образом: угол равен 360 градусов деленных на количество оснований. В случае правильной четырехугольной пирамиды, одна четверть от 360 градусов равна 90 градусам, поэтому угол в такой пирамиде равен 90 градусам.
Угол в правильной четырехугольной пирамиде является прямым углом, что делает ее особенной и отличает от других пирамид. Подобная конструкция пирамиды встречается в архитектуре, геометрии и строительстве, где прямой угол является базовым элементом для построения переходов и прямых соединений.
Равенство углов в правильной пирамиде
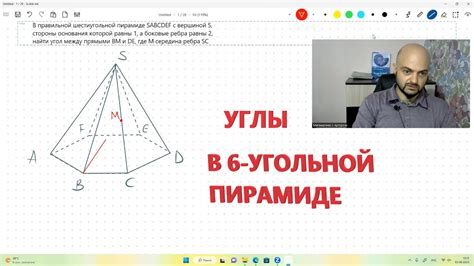
Все углы при вершине пирамиды также равны между собой и равны 360 градусов, так как сумма всех углов вокруг вершины равна 360 градусов. Следовательно, угол в вершине пирамиды равен 360 градусов деленных на количество боковых граней пирамиды.
Например, в правильной четырехугольной пирамиде, угол в вершине будет равен 360 градусов деленных на 4, что равно 90 градусам.
Таким образом, в правильной пирамиде, угол в вершине будет равен 360 градусов деленных на количество боковых граней пирамиды.
Угол между боковой гранью и основанием
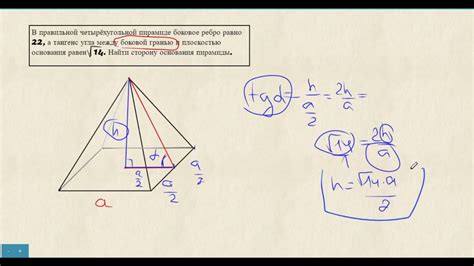
Угол между боковой гранью и основанием является важной характеристикой, определяющей форму и структуру пирамиды. Он влияет на взаимное расположение граней пирамиды и определяет углы, под которыми основание видно из различных точек зрения.
Изучение угла между боковой гранью и основанием позволяет более глубоко понять геометрические свойства правильных пирамид и использовать их в различных математических и технических задачах.



